Question Number 66827 by mr W last updated on 20/Aug/19

Commented by mr W last updated on 20/Aug/19

$${the}\:{graph}\:{above}\:{shows}\:{the}\:{equation} \\ $$$$\frac{\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\frac{\mathrm{ln}\:\left({y}+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }} \\ $$$$ \\ $$$${it}\:{contains}\:{in}\:{fact}\:{two}\:{curves}: \\ $$$${curve}\:\mathrm{1}:\:{y}={x}\:{which}\:{always}\:{fulfills} \\ $$$${the}\:{equation} \\ $$$${curve}\:\mathrm{2}:\:{y}=??? \\ $$$$ \\ $$$${can}\:{you}\:{find}\:{the}\:{function}\:{for}\:{curve}\:\mathrm{2} \\ $$$${in}\:{form}\:{of}\:{y}={f}\left({x}\right)? \\ $$$${can}\:{you}\:{find}\:{the}\:{intersection}\:{point} \\ $$$${of}\:{both}\:{curves}?\:{i}\:{mean}\:{with}\:{exact} \\ $$$${values}? \\ $$
Commented by Prithwish sen last updated on 23/Aug/19

$$\mathrm{Sir}\:,\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{process}\:\mathrm{of}\:\mathrm{decomposing} \\ $$$$\mathrm{such}\:\mathrm{functions}\:? \\ $$
Commented by mr W last updated on 24/Aug/19
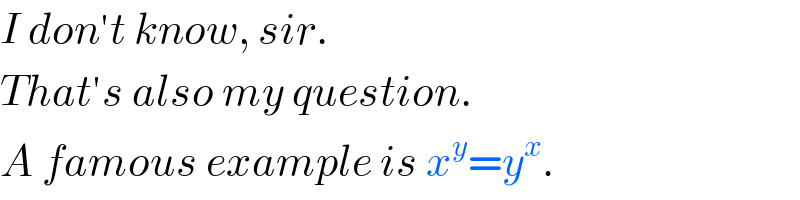
$${I}\:{don}'{t}\:{know},\:{sir}. \\ $$$${That}'{s}\:{also}\:{my}\:{question}. \\ $$$${A}\:{famous}\:{example}\:{is}\:{x}^{{y}} ={y}^{{x}} . \\ $$
