Question Number 66852 by John Kaloki Musau last updated on 20/Aug/19
Commented by John Kaloki Musau last updated on 20/Aug/19
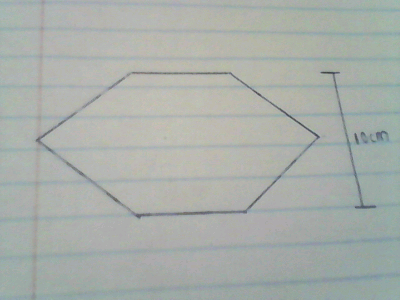
The cross-section of a head of a bolt is the form of a regular hexagon as shown in the figure below. Determine the area of the cross-section.
Commented by John Kaloki Musau last updated on 20/Aug/19
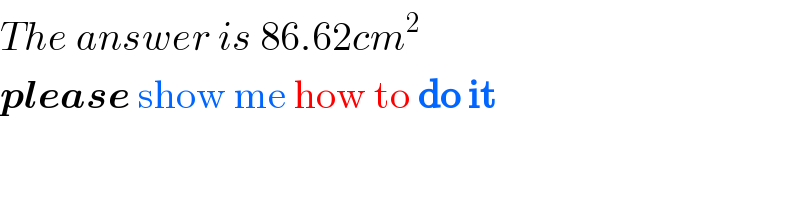
$${The}\:{answer}\:{is}\:\mathrm{86}.\mathrm{62}{cm}^{\mathrm{2}} \\ $$$$\boldsymbol{{please}}\:\mathrm{show}\:\mathrm{me}\:\mathrm{how}\:\mathrm{to}\:\boldsymbol{\mathrm{do}}\:\boldsymbol{\mathrm{it}} \\ $$
Commented by Prithwish sen last updated on 20/Aug/19
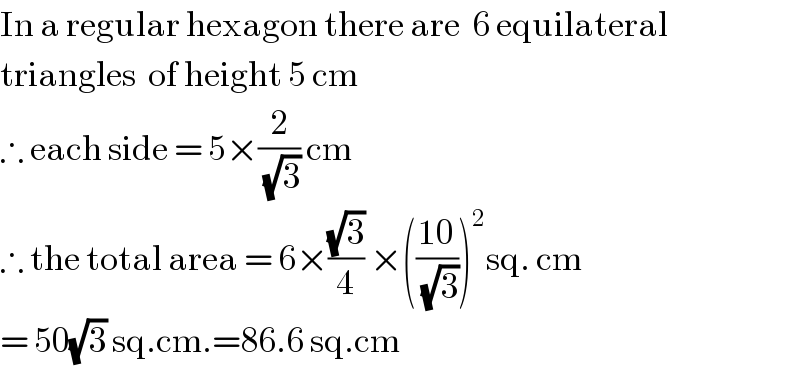
$$\mathrm{In}\:\mathrm{a}\:\mathrm{regular}\:\mathrm{hexagon}\:\mathrm{there}\:\mathrm{are}\:\:\mathrm{6}\:\mathrm{equilateral} \\ $$$$\mathrm{triangles}\:\:\mathrm{of}\:\mathrm{height}\:\mathrm{5}\:\mathrm{cm} \\ $$$$\therefore\:\mathrm{each}\:\mathrm{side}\:=\:\mathrm{5}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{cm} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{total}\:\mathrm{area}\:=\:\mathrm{6}×\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\:×\left(\frac{\mathrm{10}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \mathrm{sq}.\:\mathrm{cm} \\ $$$$=\:\mathrm{50}\sqrt{\mathrm{3}}\:\mathrm{sq}.\mathrm{cm}.=\mathrm{86}.\mathrm{6}\:\mathrm{sq}.\mathrm{cm} \\ $$
