Question Number 66937 by Cmr 237 last updated on 20/Aug/19
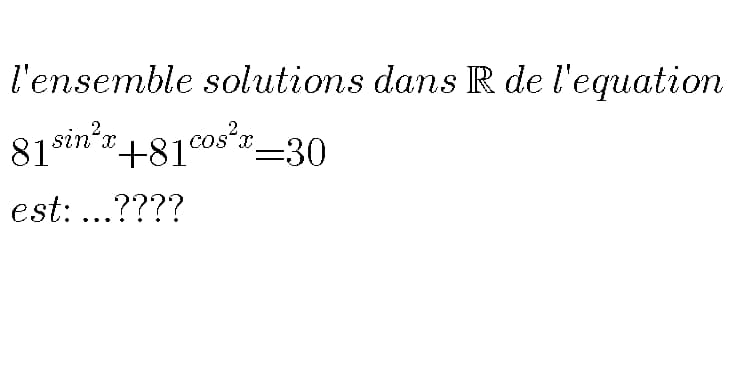
Answered by mr W last updated on 21/Aug/19
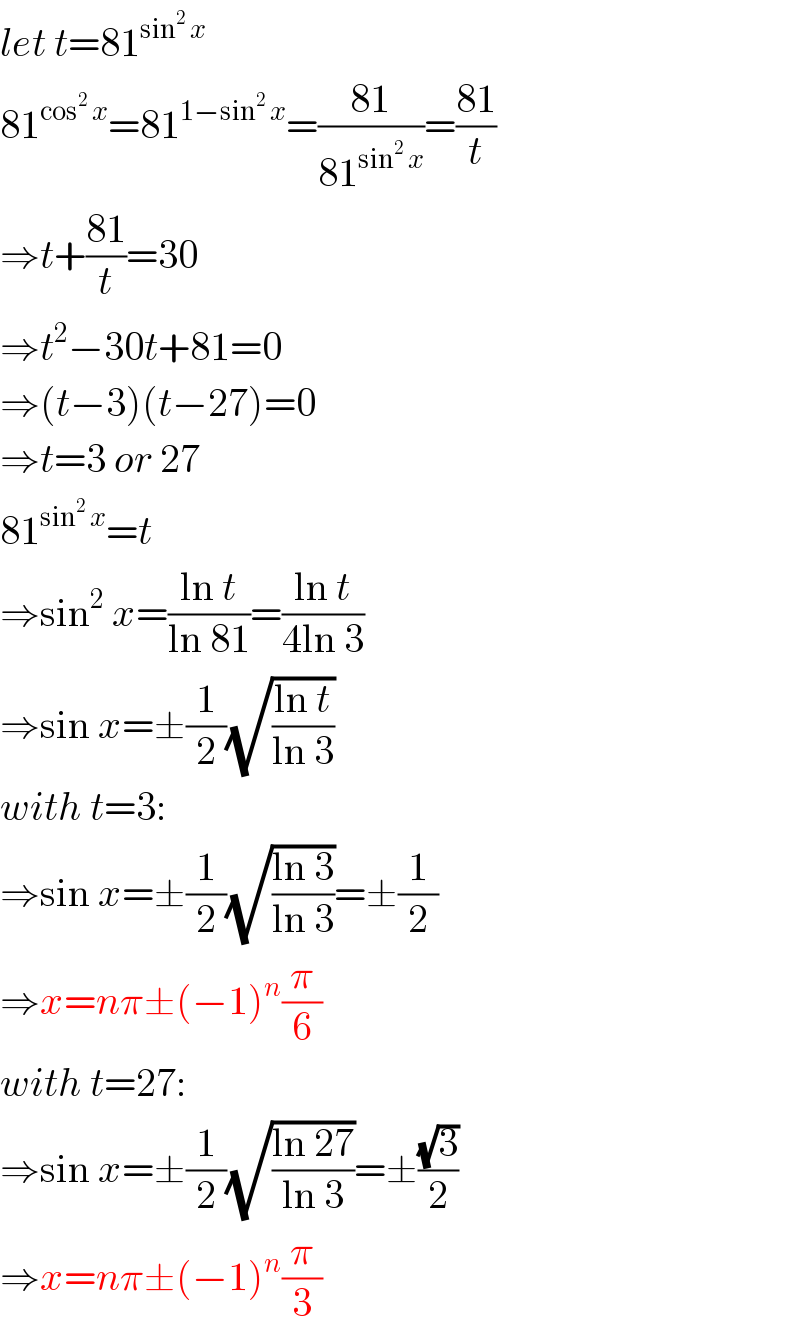
$${let}\:{t}=\mathrm{81}^{\mathrm{sin}^{\mathrm{2}} \:{x}} \\ $$$$\mathrm{81}^{\mathrm{cos}^{\mathrm{2}} \:{x}} =\mathrm{81}^{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}} =\frac{\mathrm{81}}{\mathrm{81}^{\mathrm{sin}^{\mathrm{2}} \:{x}} }=\frac{\mathrm{81}}{{t}} \\ $$$$\Rightarrow{t}+\frac{\mathrm{81}}{{t}}=\mathrm{30} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{30}{t}+\mathrm{81}=\mathrm{0} \\ $$$$\Rightarrow\left({t}−\mathrm{3}\right)\left({t}−\mathrm{27}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{3}\:{or}\:\mathrm{27} \\ $$$$\mathrm{81}^{\mathrm{sin}^{\mathrm{2}} \:{x}} ={t} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:{x}=\frac{\mathrm{ln}\:{t}}{\mathrm{ln}\:\mathrm{81}}=\frac{\mathrm{ln}\:{t}}{\mathrm{4ln}\:\mathrm{3}} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{ln}\:{t}}{\mathrm{ln}\:\mathrm{3}}} \\ $$$${with}\:{t}=\mathrm{3}: \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{3}}}=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}={n}\pi\pm\left(−\mathrm{1}\right)^{{n}} \frac{\pi}{\mathrm{6}} \\ $$$${with}\:{t}=\mathrm{27}: \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{ln}\:\mathrm{27}}{\mathrm{ln}\:\mathrm{3}}}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}={n}\pi\pm\left(−\mathrm{1}\right)^{{n}} \frac{\pi}{\mathrm{3}} \\ $$
Commented by Cmr 237 last updated on 21/Aug/19

$$\mathrm{thank}\:\mathrm{sir} \\ $$
