Question Number 66969 by mr W last updated on 21/Aug/19

Commented by mr W last updated on 21/Aug/19
$${Question}\:{from}\:{B}.{E}.{H}.{I}.\:{sir}\:{reposted}. \\ $$
Answered by mr W last updated on 21/Aug/19
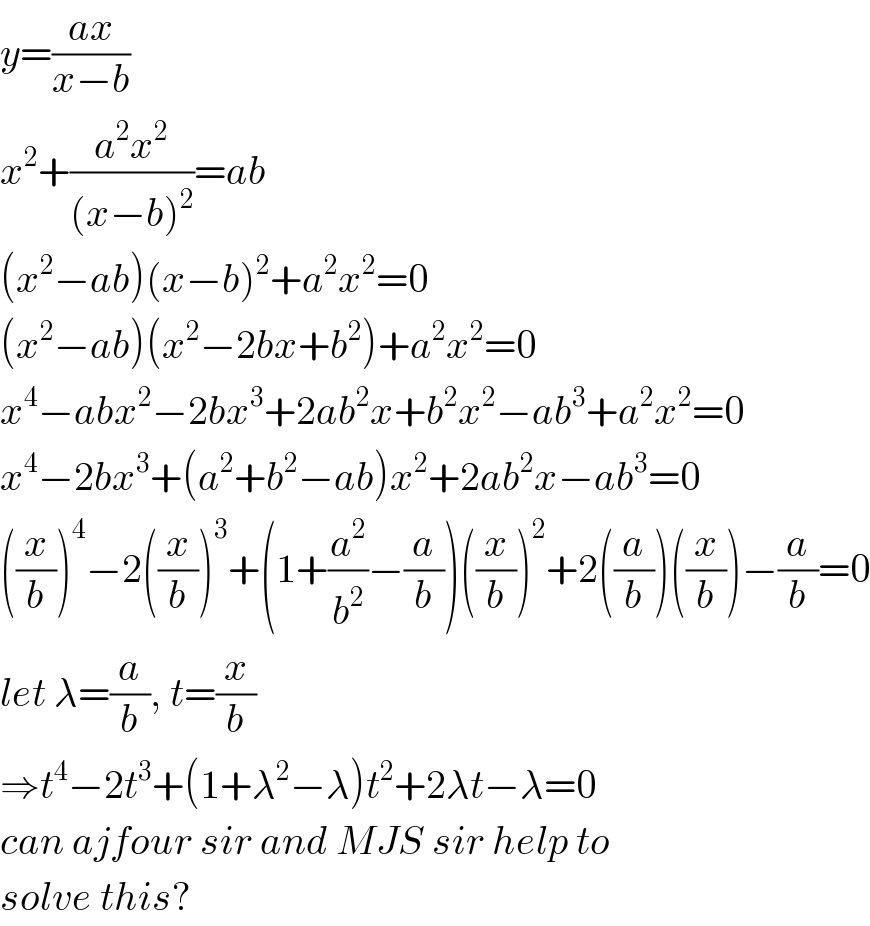
$${y}=\frac{{ax}}{{x}−{b}} \\ $$$${x}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {x}^{\mathrm{2}} }{\left({x}−{b}\right)^{\mathrm{2}} }={ab} \\ $$$$\left({x}^{\mathrm{2}} −{ab}\right)\left({x}−{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −{ab}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{bx}+{b}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} −{abx}^{\mathrm{2}} −\mathrm{2}{bx}^{\mathrm{3}} +\mathrm{2}{ab}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {x}^{\mathrm{2}} −{ab}^{\mathrm{3}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} −\mathrm{2}{bx}^{\mathrm{3}} +\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right){x}^{\mathrm{2}} +\mathrm{2}{ab}^{\mathrm{2}} {x}−{ab}^{\mathrm{3}} =\mathrm{0} \\ $$$$\left(\frac{{x}}{{b}}\right)^{\mathrm{4}} −\mathrm{2}\left(\frac{{x}}{{b}}\right)^{\mathrm{3}} +\left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)\left(\frac{{x}}{{b}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{{a}}{{b}}\right)\left(\frac{{x}}{{b}}\right)−\frac{{a}}{{b}}=\mathrm{0} \\ $$$${let}\:\lambda=\frac{{a}}{{b}},\:{t}=\frac{{x}}{{b}} \\ $$$$\Rightarrow{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} +\left(\mathrm{1}+\lambda^{\mathrm{2}} −\lambda\right){t}^{\mathrm{2}} +\mathrm{2}\lambda{t}−\lambda=\mathrm{0} \\ $$$${can}\:{ajfour}\:{sir}\:{and}\:{MJS}\:{sir}\:{help}\:{to} \\ $$$${solve}\:{this}? \\ $$
