Question-67026

Question Number 67026 by TawaTawa last updated on 21/Aug/19

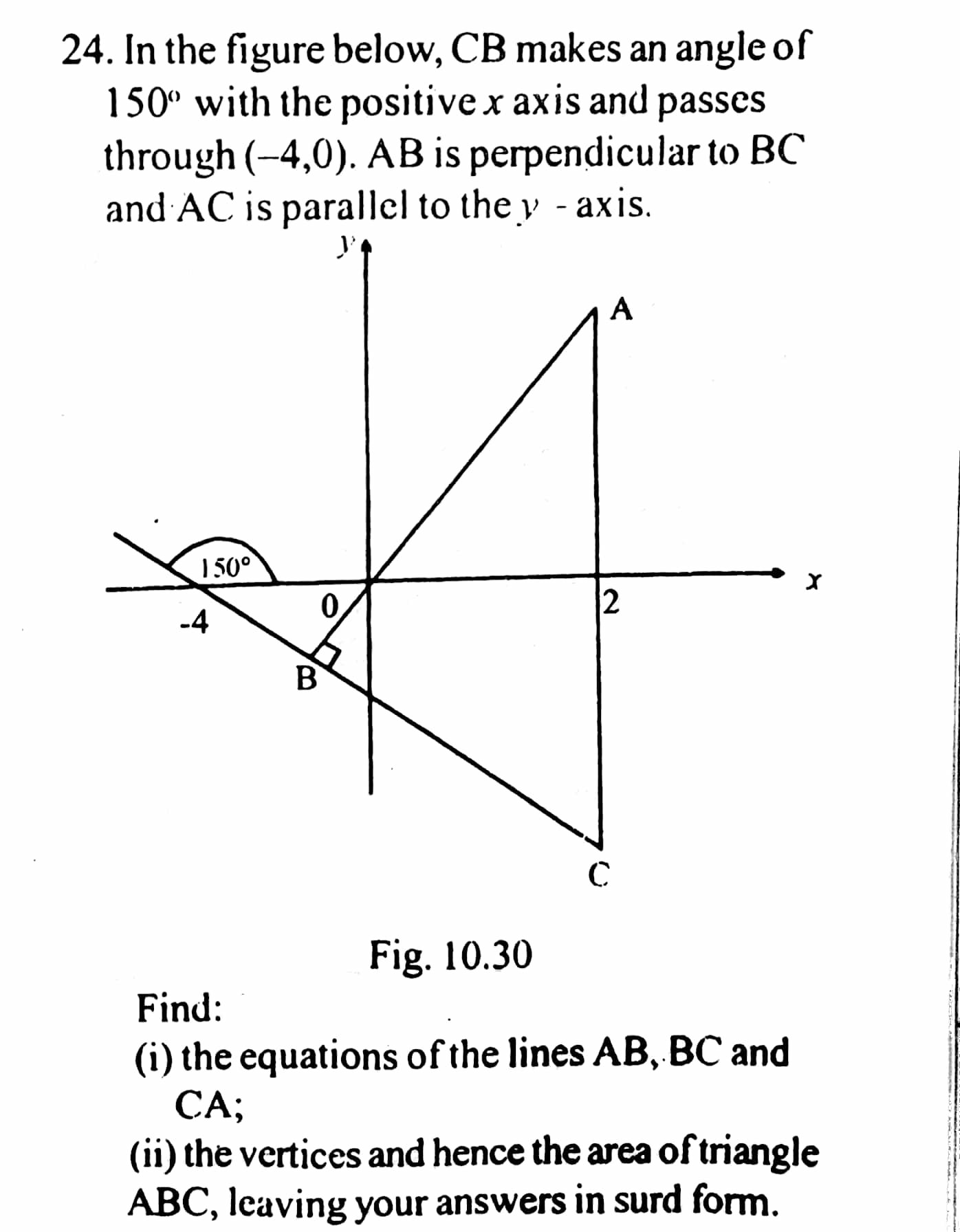
Commented by Tony Lin last updated on 22/Aug/19

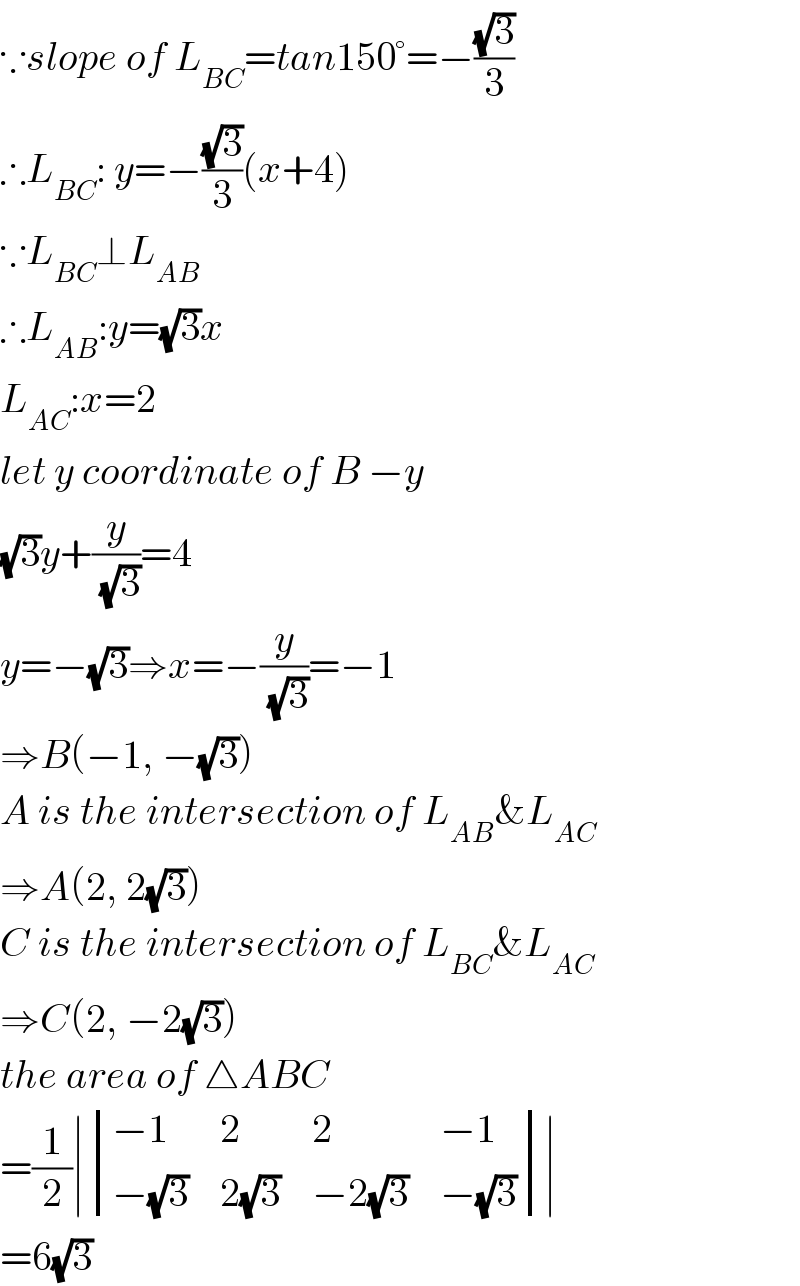
∵slope of L_(BC) =tan150°=−((√3)/3) ∴L_(BC) : y=−((√3)/3)(x+4) ∵L_(BC) ⊥L_(AB) ∴L_(AB) :y=(√3)x L_(AC) :x=2 let y coordinate of B −y (√3)y+(y/( (√3)))=4 y=−(√3)⇒x=−(y/( (√3)))=−1 ⇒B(−1, −(√3)) A is the intersection of L_(AB) &L_(AC) ⇒A(2, 2(√3)) C is the intersection of L_(BC) &L_(AC) ⇒C(2, −2(√3)) the area of △ABC =(1/2)∣ determinant (((−1),2,2,(−1)),((−(√3)),(2(√3)),(−2(√3)),(−(√3))))∣ =6(√3)

$$\because{slope}\:{of}\:{L}_{{BC}} ={tan}\mathrm{150}°=−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\therefore{L}_{{BC}} :\:{y}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left({x}+\mathrm{4}\right) \\ $$$$\because{L}_{{BC}} \bot{L}_{{AB}} \\ $$$$\therefore{L}_{{AB}} :{y}=\sqrt{\mathrm{3}}{x} \\ $$$${L}_{{AC}} :{x}=\mathrm{2} \\ $$$${let}\:{y}\:{coordinate}\:{of}\:{B}\:−{y} \\ $$$$\sqrt{\mathrm{3}}{y}+\frac{{y}}{\:\sqrt{\mathrm{3}}}=\mathrm{4} \\ $$$${y}=−\sqrt{\mathrm{3}}\Rightarrow{x}=−\frac{{y}}{\:\sqrt{\mathrm{3}}}=−\mathrm{1} \\ $$$$\Rightarrow{B}\left(−\mathrm{1},\:−\sqrt{\mathrm{3}}\right) \\ $$$${A}\:{is}\:{the}\:{intersection}\:{of}\:{L}_{{AB}} \&{L}_{{AC}} \\ $$$$\Rightarrow{A}\left(\mathrm{2},\:\mathrm{2}\sqrt{\mathrm{3}}\right) \\ $$$${C}\:{is}\:{the}\:{intersection}\:{of}\:{L}_{{BC}} \&{L}_{{AC}} \\ $$$$\Rightarrow{C}\left(\mathrm{2},\:−\mathrm{2}\sqrt{\mathrm{3}}\right) \\ $$$${the}\:{area}\:{of}\:\bigtriangleup{ABC} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{−\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}}&{−\mathrm{1}}\\{−\sqrt{\mathrm{3}}}&{\mathrm{2}\sqrt{\mathrm{3}}}&{−\mathrm{2}\sqrt{\mathrm{3}}}&{−\sqrt{\mathrm{3}}}\end{vmatrix}\mid \\ $$$$=\mathrm{6}\sqrt{\mathrm{3}} \\ $$

Commented by TawaTawa last updated on 22/Aug/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by TawaTawa last updated on 22/Aug/19

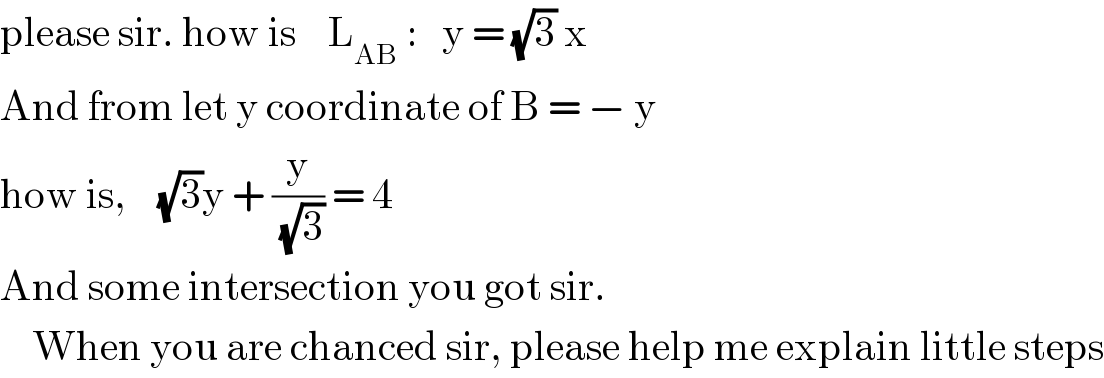
please sir. how is L_(AB) : y = (√3) x And from let y coordinate of B = − y how is, (√3)y + (y/( (√3))) = 4 And some intersection you got sir. When you are chanced sir, please help me explain little steps

$$\mathrm{please}\:\mathrm{sir}.\:\mathrm{how}\:\mathrm{is}\:\:\:\:\mathrm{L}_{\mathrm{AB}} \::\:\:\:\mathrm{y}\:=\:\sqrt{\mathrm{3}}\:\mathrm{x} \\ $$$$\mathrm{And}\:\mathrm{from}\:\mathrm{let}\:\mathrm{y}\:\mathrm{coordinate}\:\mathrm{of}\:\mathrm{B}\:=\:−\:\mathrm{y} \\ $$$$\mathrm{how}\:\mathrm{is},\:\:\:\:\sqrt{\mathrm{3}}\mathrm{y}\:+\:\frac{\mathrm{y}}{\:\sqrt{\mathrm{3}}}\:=\:\mathrm{4} \\ $$$$\mathrm{And}\:\mathrm{some}\:\mathrm{intersection}\:\mathrm{you}\:\mathrm{got}\:\mathrm{sir}.\: \\ $$$$\:\:\:\:\mathrm{When}\:\mathrm{you}\:\mathrm{are}\:\mathrm{chanced}\:\mathrm{sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{explain}\:\mathrm{little}\:\mathrm{steps} \\ $$

Commented by Tony Lin last updated on 22/Aug/19