Menu Close

Question-67035

Tinku Tara 0 Comments
Pin




Question Number 67035 by rajesh4661kumar@gmail.com last updated on 22/Aug/19
Commented by rajesh4661kumar@gmail.com last updated on 22/Aug/19
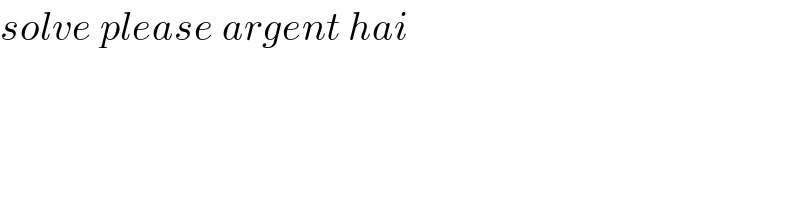
solve please argent hai
$${solve}\:{please}\:{argent}\:{hai} \\ $$
Commented by mathmax by abdo last updated on 22/Aug/19
let I =∫ (dx/(x^4 −x^2 +1)) ⇒I =∫ (dx/((x^2 +1)^2 −3x^2 ))=∫ (dx/((x^2 +1−(√3)x)(x^2 +1+(√3)x))) let decompose F(x)=(1/((x^2 −(√3)x +1)(x^2 +(√3)x +1))) ⇒ F(x)=((ax+b)/(x^2 −(√3)x +1)) +((cx+d)/(x^2 +(√3)x +1)) F(−x)=F(x) ⇒ ((−ax+b)/(x^2 +(√3)x+1)) +((−cx+d)/(x^2 −(√3)x +1)) =F(x) ⇒c=−a and b=d ⇒F(x) =((ax+b)/(x^2 −(√3)x +1)) +((−ax +b)/(x^2 +(√3)x +1)) F(0) =1 =2b ⇒b=(1/2) F(1) =((a+b)/(2−(√3))) +((−a+b)/(2+(√3))) =1 ⇒(2+(√3))(a+(1/2))+(2−(√3))(−a+(1/2))=1⇒ ⇒(2+(√3))a +((2+(√3))/2) −(2−(√3))a +((2−(√3))/2) =1 ⇒ 2(√3)a +2 =1 ⇒2(√3)a =−1 ⇒ a =−(1/(2(√3))) ⇒ F(x) =(1/2) ((−(1/( (√3)))x+1)/(x^2 −(√3)x+1)) +(1/2)(((1/( (√3) ))x+1)/(x^2 +(√3)x +1)) ⇒ ∫ F(x)dx =(1/(2(√3))) ∫ ((x+(√3))/(x^2 +(√3)x +1))−(1/(2(√3))) ∫ ((x−(√3))/(x^2 −(√3)x+1)) =H−K H=∫ ((x+(√3))/(x^2 +(√3)x +1)) =(1/2) ∫ ((2x+2(√3))/(x^2 +(√3)x +1)) =(1/2)ln(x^2 +(√3)x +1)+((√3)/2)∫(dx/(x^2 +(√3)x +1)) ∫ (dx/(x^2 +(√3)x +1)) =∫ (dx/(x^2 +2((√3)/2)x +(3/4) +1−(3/4))) =∫ (dx/((x+((√3)/2))^2 +(1/4))) =_(x+((√3)/2)=(t/2)) 4∫ (1/(t^2 +1)) (dt/2) =2 arctan(2x+(√3)) ⇒ H =(1/(2(√3)))×(1/2)ln(x^2 +(√3)x +1)+(1/(2(√3)))×((√3)/2) ×2 arctan(2x+(√3)) =(1/(4(√3)))ln(x^2 +(√3)x +1)+(1/2) arctan(2x+(√3)) K=(1/(2(√3)))∫ ((x−(√3))/(x^2 −(√3)x+1)) dx =_(x =−t) (1/(2(√3))) ∫ ((−t−(√3))/(t^2 +(√3)t +1))(−dt) =(1/(2(√3)))∫ ((t+(√3))/(t^2 +(√3)t +1))dt =(1/(4(√3)))ln(x^2 −(√3)x+1)+(1/2)arctan(−2x+(√3)) ⇒ I =(1/(4(√3)))ln(x^2 +(√3)x+1)+(1/2) arctan(2x+(√3)) −(1/(4(√3)))ln(x^2 −(√3)x+1)+(1/2) arctan(2x−(√3)) +C I=(1/(4(√3)))ln(((x^2 +(√3)x +1)/(x^2 −(√3)x +1))) +(1/2){ arctan(2x+(√3)) +arctan(2x−(√3))} +C
$${let}\:{I}\:=\int\:\:\frac{{dx}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{I}\:=\int\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{2}} }=\int\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{3}}{x}\right)\left({x}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{3}}{x}\right)} \\ $$$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}\:+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}\:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{ax}+{b}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}} \\ $$$${F}\left(−{x}\right)={F}\left({x}\right)\:\Rightarrow\:\frac{−{ax}+{b}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}\:+\frac{−{cx}+{d}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\:={F}\left({x}\right)\:\Rightarrow{c}=−{a}\:{and}\:{b}={d} \\ $$$$\Rightarrow{F}\left({x}\right)\:=\frac{{ax}+{b}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\:+\frac{−{ax}\:+{b}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\mathrm{2}{b}\:\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{{a}+{b}}{\mathrm{2}−\sqrt{\mathrm{3}}}\:+\frac{−{a}+{b}}{\mathrm{2}+\sqrt{\mathrm{3}}}\:=\mathrm{1}\:\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left(−{a}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{1}\Rightarrow \\ $$$$\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){a}\:+\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:−\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){a}\:+\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}{a}\:\:+\mathrm{2}\:=\mathrm{1}\:\Rightarrow\mathrm{2}\sqrt{\mathrm{3}}{a}\:=−\mathrm{1}\:\Rightarrow\:{a}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\int\:\frac{{x}+\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\int\:\:\:\frac{{x}−\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\:={H}−{K} \\ $$$${H}=\int\:\:\frac{{x}+\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{2}{x}+\mathrm{2}\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}} \\ $$$$\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\:=\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\:+\frac{\mathrm{3}}{\mathrm{4}}\:+\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}}\:=\int\:\:\:\frac{{dx}}{\left({x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=_{{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{{t}}{\mathrm{2}}} \:\:\:\:\mathrm{4}\int\:\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{{dt}}{\mathrm{2}}\:=\mathrm{2}\:{arctan}\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\:\Rightarrow \\ $$$${H}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:×\mathrm{2}\:{arctan}\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}{ln}\left({x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}\:+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right) \\ $$$${K}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\:\:\frac{{x}−\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\:{dx}\:=_{{x}\:=−{t}} \frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\:\:\int\:\frac{−{t}−\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}\:+\mathrm{1}}\left(−{dt}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\:\:\:\frac{{t}+\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}\:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}{ln}\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(−\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}{ln}\left({x}^{\mathrm{2}} \:+\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}{ln}\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\:+{C} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}{ln}\left(\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}\:+\mathrm{1}}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{arctan}\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\:+{arctan}\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\right\}\:+{C} \\ $$
Answered by Tanmay chaudhury last updated on 22/Aug/19

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *