Question-67071

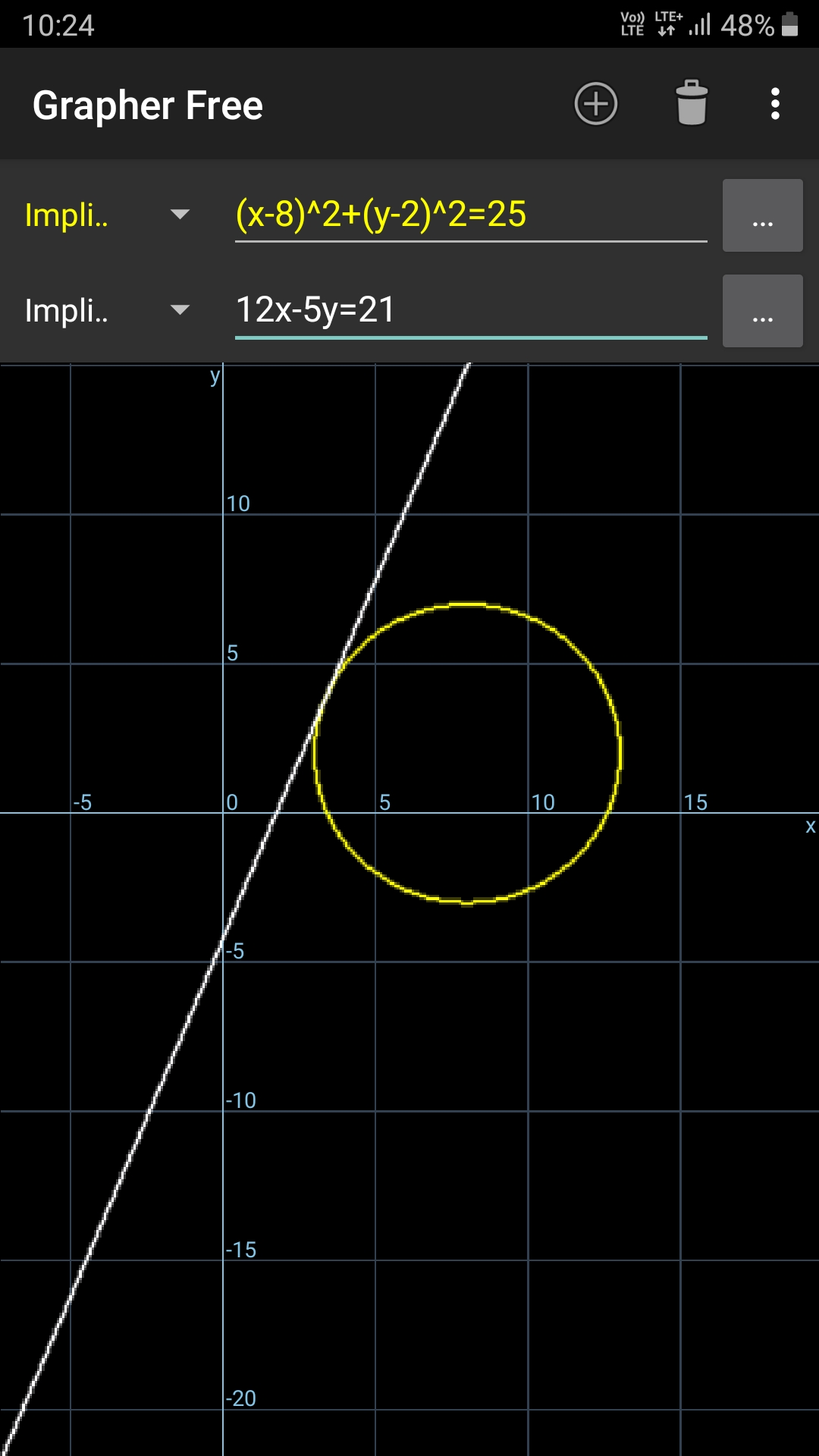
Question Number 67071 by TawaTawa last updated on 22/Aug/19

Commented by Prithwish sen last updated on 22/Aug/19

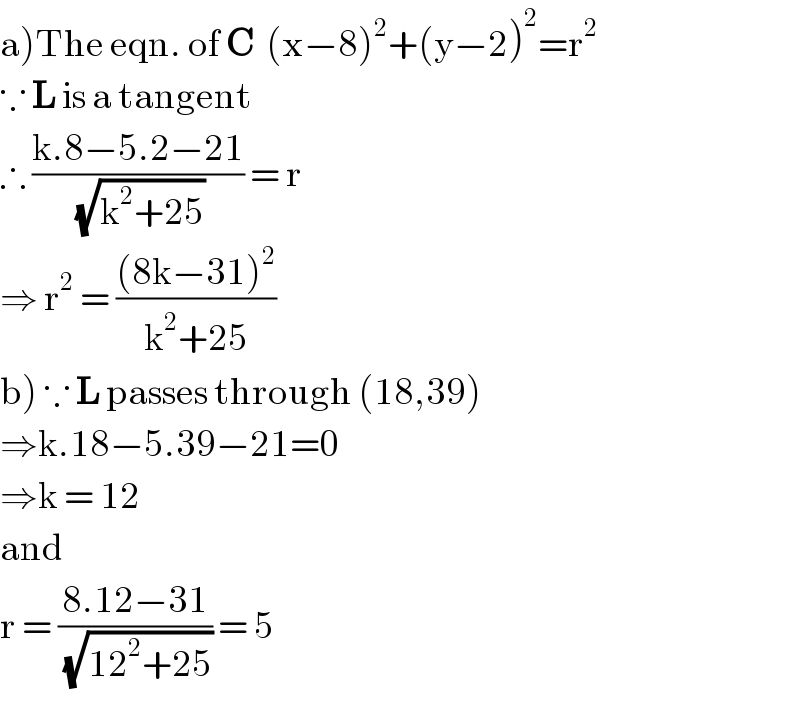
a)The eqn. of C (x−8)^2 +(y−2)^2 =r^2 ∵ L is a tangent ∴ ((k.8−5.2−21)/( (√(k^2 +25)))) = r ⇒ r^2 = (((8k−31)^2 )/(k^2 +25)) b) ∵ L passes through (18,39) ⇒k.18−5.39−21=0 ⇒k = 12 and r = ((8.12−31)/( (√(12^2 +25)))) = 5

$$\left.\mathrm{a}\right)\mathrm{The}\:\mathrm{eqn}.\:\mathrm{of}\:\boldsymbol{\mathrm{C}}\:\:\left(\mathrm{x}−\mathrm{8}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} \\ $$$$\because\:\boldsymbol{\mathrm{L}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{tangent} \\ $$$$\therefore\:\frac{\mathrm{k}.\mathrm{8}−\mathrm{5}.\mathrm{2}−\mathrm{21}}{\:\sqrt{\mathrm{k}^{\mathrm{2}} +\mathrm{25}}}\:=\:\mathrm{r} \\ $$$$\Rightarrow\:\mathrm{r}^{\mathrm{2}} \:=\:\frac{\left(\mathrm{8k}−\mathrm{31}\right)^{\mathrm{2}} }{\mathrm{k}^{\mathrm{2}} +\mathrm{25}} \\ $$$$\left.\mathrm{b}\right)\:\because\:\boldsymbol{\mathrm{L}}\:\mathrm{passes}\:\mathrm{through}\:\left(\mathrm{18},\mathrm{39}\right) \\ $$$$\Rightarrow\mathrm{k}.\mathrm{18}−\mathrm{5}.\mathrm{39}−\mathrm{21}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{k}\:=\:\mathrm{12} \\ $$$$\mathrm{and} \\ $$$$\mathrm{r}\:=\:\frac{\mathrm{8}.\mathrm{12}−\mathrm{31}}{\:\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{25}}}\:=\:\mathrm{5} \\ $$

Commented by TawaTawa last updated on 22/Aug/19

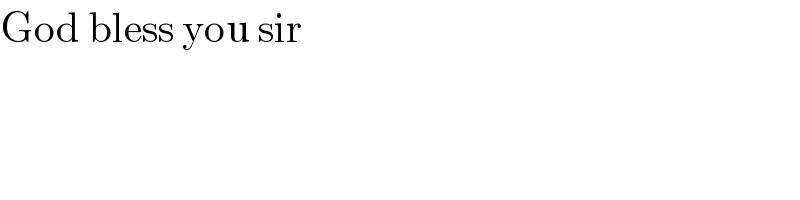
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by TawaTawa last updated on 22/Aug/19

$$\mathrm{I}\:\mathrm{appreciate} \\ $$

Commented by TawaTawa last updated on 22/Aug/19

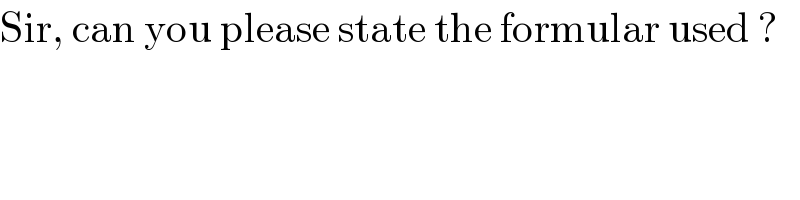
Sir, can you please state the formular used ?

$$\mathrm{Sir},\:\mathrm{can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{state}\:\mathrm{the}\:\mathrm{formular}\:\mathrm{used}\:? \\ $$

Commented by TawaTawa last updated on 22/Aug/19

$$\mathrm{Probably}\:\mathrm{sketch}\:\mathrm{sir} \\ $$

Commented by Prithwish sen last updated on 22/Aug/19

a) The equation of a circle with (a,b) as it center and r as its radius is (x−a)^2 +(y−b)^2 =r^2 ∵ L is the tangent . Then the tangent of a circle is always perpendicular to its radius at the same point. So I just equating the perendicular distance from (8,2) to the tangent L with its radius r.

$$\left.\mathrm{a}\right)\:\mathrm{The}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{with}\:\left(\mathrm{a},\mathrm{b}\right)\:\mathrm{as}\:\mathrm{it}\: \\ $$$$\mathrm{center}\:\mathrm{and}\:\mathrm{r}\:\mathrm{as}\:\mathrm{its}\:\mathrm{radius}\:\mathrm{is}\: \\ $$$$\:\:\:\:\left(\mathrm{x}−\mathrm{a}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{b}\right)^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} \\ $$$$\because\:\mathrm{L}\:\mathrm{is}\:\mathrm{the}\:\mathrm{tangent}\:.\:\mathrm{Then}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{of}\:\mathrm{a}\: \\ $$$$\mathrm{circle}\:\mathrm{is}\:\mathrm{always}\:\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{its}\:\mathrm{radius} \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{same}\:\mathrm{point}.\:\mathrm{So}\:\mathrm{I}\:\mathrm{just}\:\mathrm{equating}\:\mathrm{the}\: \\ $$$$\mathrm{perendicular}\:\mathrm{distance}\:\mathrm{from}\:\left(\mathrm{8},\mathrm{2}\right)\:\mathrm{to}\:\mathrm{the}\: \\ $$$$\mathrm{tangent}\:\mathrm{L}\:\mathrm{with}\:\mathrm{its}\:\mathrm{radius}\:\mathrm{r}. \\ $$

Commented by Prithwish sen last updated on 22/Aug/19

Facebook Tweet Pin

Leave a Reply Cancel reply