Question Number 67193 by Rasheed.Sindhi last updated on 23/Aug/19

Commented by Rasheed.Sindhi last updated on 24/Aug/19

$$\:\underset{−} {\:\:\:\:\:\:\:\:\:\:\mathbb{S}\mathrm{ome}\:\mathbb{C}\mathrm{ounting}\:\mathbb{P}\mathrm{roblems}\:\:\:\:\:\:\:\:\:\:} \\ $$$$\left({a}\right){How}\:{many}\:{rectangles}\:{are}\:{in}\:{the} \\ $$$$\:\:\:\:\:\:\:{above}\:{picture}? \\ $$$$\left({b}\right){How}\:{many}\:{rectangles}\:{contain} \\ $$$$\:\:\:\:\:\:{vertex}\:\mathrm{L}? \\ $$$$\left({c}\right){How}\:{many}\:{rectangles}\:{contain} \\ $$$$\:\:\:\:\:\:\overline {{GQ}}\:{as}\:{an}\:\:{edge}? \\ $$
Commented by Tony Lin last updated on 24/Aug/19

$$\left(\mathrm{1}\right){C}_{\mathrm{2}} ^{\mathrm{7}} {C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{210} \\ $$$${choose}\:{two}\:{from}\:{seven}\:{vertical}\:{lines}\: \\ $$$${choose}\:{two}\:{from}\:{five}\:{horizontal}\:{lines} \\ $$$$\left(\mathrm{2}\right){C}_{\mathrm{1}} ^{\mathrm{6}} {C}_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{24} \\ $$$${choose}\:{one}\:{vertical}\:{line}\:{except}\:{OK} \\ $$$${choose}\:{one}\:{horizontal}\:{line}\:{except}\:{BH}_{\mathrm{1}} \\ $$$${then}\:{L}\:{would}\:{be}\:{a}\:{vertex}\:{of}\:{rectangles} \\ $$$$\left(\mathrm{3}\right){C}_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{4} \\ $$$${choose}\:{one}\:{from}\:{JT},\:{IS},{HR\&FP} \\ $$$${then}\:{GQ}\:{would}\:{be}\:{an}\:{edge}\:{of}\:{rectangles} \\ $$
Commented by mr W last updated on 24/Aug/19
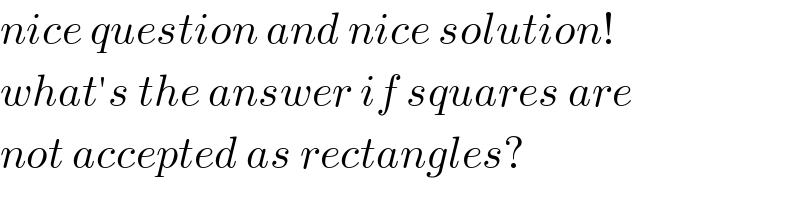
$${nice}\:{question}\:{and}\:{nice}\:{solution}! \\ $$$${what}'{s}\:{the}\:{answer}\:{if}\:{squares}\:{are} \\ $$$${not}\:{accepted}\:{as}\:{rectangles}? \\ $$
Commented by Tony Lin last updated on 24/Aug/19
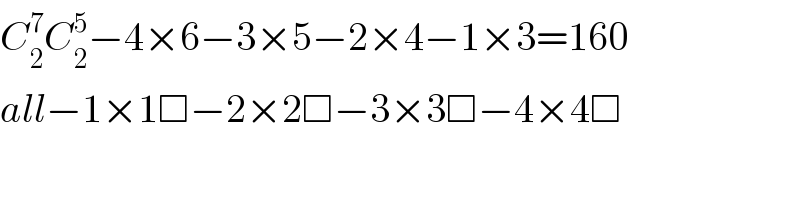
$${C}_{\mathrm{2}} ^{\mathrm{7}} {C}_{\mathrm{2}} ^{\mathrm{5}} −\mathrm{4}×\mathrm{6}−\mathrm{3}×\mathrm{5}−\mathrm{2}×\mathrm{4}−\mathrm{1}×\mathrm{3}=\mathrm{160} \\ $$$${all}−\mathrm{1}×\mathrm{1}\Box−\mathrm{2}×\mathrm{2}\Box−\mathrm{3}×\mathrm{3}\Box−\mathrm{4}×\mathrm{4}\Box \\ $$
Commented by mr W last updated on 24/Aug/19

$${perfect}\:{sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 24/Aug/19
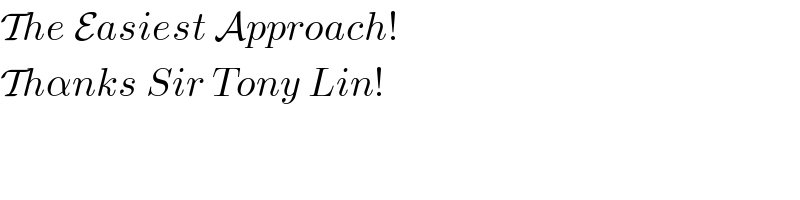
$$\mathcal{T}{he}\:\mathcal{E}{asiest}\:\mathcal{A}{pproach}! \\ $$$$\mathcal{T}{h}\alpha{nks}\:{Sir}\:{Tony}\:{Lin}! \\ $$
Commented by Rasheed.Sindhi last updated on 24/Aug/19
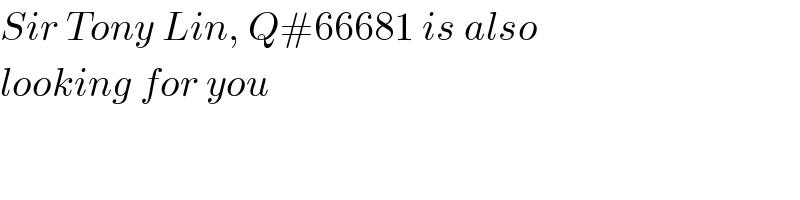
$${Sir}\:{Tony}\:{Lin},\:{Q}#\mathrm{66681}\:{is}\:{also} \\ $$$${looking}\:{for}\:{you} \\ $$
