Question Number 67307 by aliesam last updated on 25/Aug/19

Commented by mathmax by abdo last updated on 25/Aug/19

$${S}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{cos}\left({n}\theta\right)}{\mathrm{2}^{{n}} }\:\Rightarrow\:{S}\:={Re}\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{{in}\theta} }{\mathrm{2}^{{n}} }\right)\:={Re}\left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(\frac{{e}^{{i}\theta} }{\mathrm{2}}\right)^{{n}} \right) \\ $$$${we}\:{have}\:\mid\frac{{e}^{{i}\theta} }{\mathrm{2}}\mid<\mathrm{1}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{e}^{{i}\theta} }{\mathrm{2}}\right)^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\frac{{e}^{{i}\theta} }{\mathrm{2}}}\:=\frac{\mathrm{2}}{\mathrm{2}−{e}^{{i}\theta} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}−{cos}\theta\:−{isin}\theta}\:=\frac{\mathrm{2}\left(\mathrm{2}−{cos}\theta\:+{isin}\theta\right)}{\left(\mathrm{2}−{cos}\theta\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \theta}\:=\frac{\mathrm{4}−\mathrm{2}{cos}\theta\:+\mathrm{2}{i}\:{sin}\theta}{\mathrm{4}−\mathrm{4}{cos}\theta\:+\mathrm{1}} \\ $$$$=\frac{\mathrm{4}−\mathrm{2}{cos}\theta\:+\mathrm{2}{i}\:{sin}\theta}{\mathrm{5}−\mathrm{4}{cos}\theta}\:\Rightarrow\:{S}\:=\frac{\mathrm{4}−\mathrm{2}{cos}\theta}{\mathrm{5}−\mathrm{4}{cos}\theta} \\ $$
Answered by mind is power last updated on 25/Aug/19
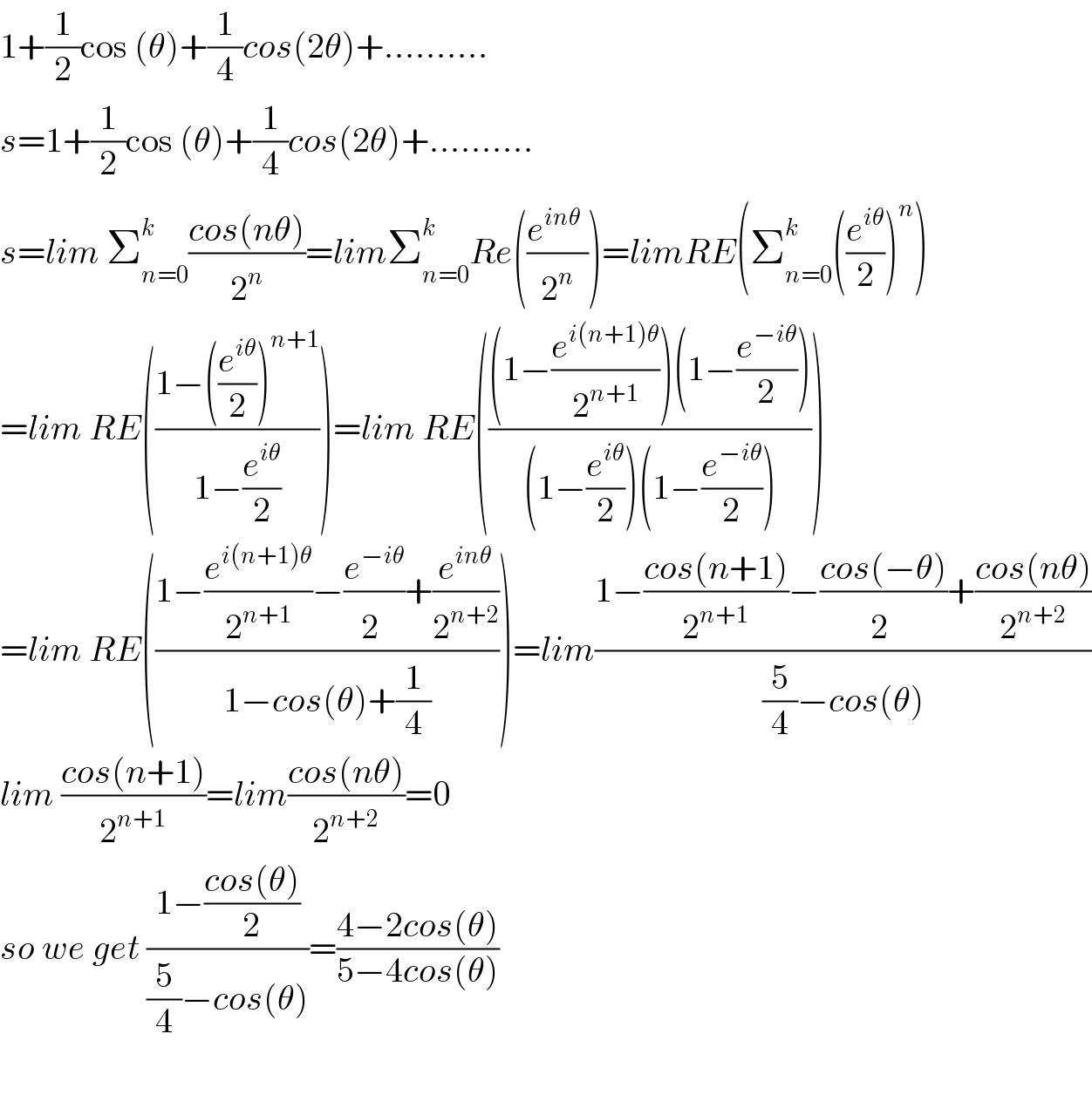
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\left(\theta\right)+\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{2}\theta\right)+………. \\ $$$${s}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\left(\theta\right)+\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{2}\theta\right)+………. \\ $$$${s}={lim}\:\sum_{{n}=\mathrm{0}} ^{{k}} \frac{{cos}\left({n}\theta\right)}{\mathrm{2}^{{n}} }={lim}\sum_{{n}=\mathrm{0}} ^{{k}} {Re}\left(\frac{{e}^{{in}\theta} \:}{\mathrm{2}^{{n}} }\right)={limRE}\left(\sum_{{n}=\mathrm{0}} ^{{k}} \left(\frac{{e}^{{i}\theta} }{\mathrm{2}}\right)^{{n}} \right) \\ $$$$={lim}\:{RE}\left(\frac{\mathrm{1}−\left(\frac{{e}^{{i}\theta} }{\mathrm{2}}\right)^{{n}+\mathrm{1}} }{\mathrm{1}−\frac{{e}^{{i}\theta} }{\mathrm{2}}}\right)={lim}\:{RE}\left(\frac{\left(\mathrm{1}−\frac{{e}^{{i}\left({n}+\mathrm{1}\right)\theta} }{\mathrm{2}^{{n}+\mathrm{1}} }\right)\left(\mathrm{1}−\frac{{e}^{−{i}\theta} }{\mathrm{2}}\right)}{\left(\mathrm{1}−\frac{{e}^{{i}\theta} }{\mathrm{2}}\right)\left(\mathrm{1}−\frac{{e}^{−{i}\theta} }{\mathrm{2}}\right)}\right) \\ $$$$={lim}\:{RE}\left(\frac{\mathrm{1}−\frac{{e}^{{i}\left({n}+\mathrm{1}\right)\theta} }{\mathrm{2}^{{n}+\mathrm{1}} }−\frac{{e}^{−{i}\theta} }{\mathrm{2}^{} }+\frac{{e}^{{in}\theta} }{\mathrm{2}^{{n}+\mathrm{2}} }}{\mathrm{1}−{cos}\left(\theta\right)+\frac{\mathrm{1}}{\mathrm{4}}}\right)={lim}\frac{\mathrm{1}−\frac{{cos}\left({n}+\mathrm{1}\right)}{\mathrm{2}^{{n}+\mathrm{1}} }−\frac{{cos}\left(−\theta\right)}{\mathrm{2}^{} }+\frac{{cos}\left({n}\theta\right)}{\mathrm{2}^{{n}+\mathrm{2}} }}{\frac{\mathrm{5}}{\mathrm{4}}−{cos}\left(\theta\right)} \\ $$$${lim}\:\frac{{cos}\left({n}+\mathrm{1}\right)}{\mathrm{2}^{{n}+\mathrm{1}} }={lim}\frac{{cos}\left({n}\theta\right)}{\mathrm{2}^{{n}+\mathrm{2}} }=\mathrm{0} \\ $$$${so}\:{we}\:{get}\:\frac{\mathrm{1}−\frac{{cos}\left(\theta\right)}{\mathrm{2}}}{\frac{\mathrm{5}}{\mathrm{4}}−{cos}\left(\theta\right)}=\frac{\mathrm{4}−\mathrm{2}{cos}\left(\theta\right)}{\mathrm{5}−\mathrm{4}{cos}\left(\theta\right)} \\ $$$$ \\ $$
