Question-67350

Question Number 67350 by TawaTawa last updated on 26/Aug/19

Commented by TawaTawa last updated on 26/Aug/19

$$\mathrm{Calculate}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}.\: \\ $$

Answered by mr W last updated on 26/Aug/19

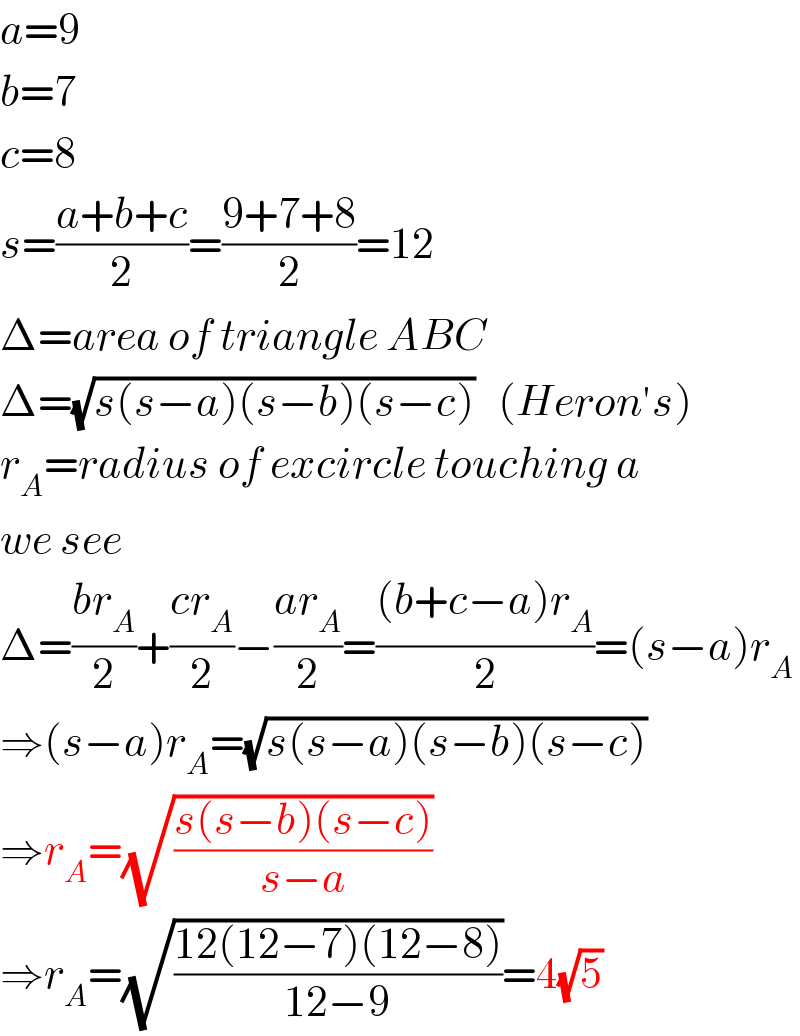
a=9 b=7 c=8 s=((a+b+c)/2)=((9+7+8)/2)=12 Δ=area of triangle ABC Δ=(√(s(s−a)(s−b)(s−c))) (Heron′s) r_A =radius of excircle touching a we see Δ=((br_A )/2)+((cr_A )/2)−((ar_A )/2)=(((b+c−a)r_A )/2)=(s−a)r_A ⇒(s−a)r_A =(√(s(s−a)(s−b)(s−c))) ⇒r_A =(√((s(s−b)(s−c))/(s−a))) ⇒r_A =(√((12(12−7)(12−8))/(12−9)))=4(√5)

$${a}=\mathrm{9} \\ $$$${b}=\mathrm{7} \\ $$$${c}=\mathrm{8} \\ $$$${s}=\frac{{a}+{b}+{c}}{\mathrm{2}}=\frac{\mathrm{9}+\mathrm{7}+\mathrm{8}}{\mathrm{2}}=\mathrm{12} \\ $$$$\Delta={area}\:{of}\:{triangle}\:{ABC} \\ $$$$\Delta=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}\:\:\:\left({Heron}'{s}\right) \\ $$$${r}_{{A}} ={radius}\:{of}\:{excircle}\:{touching}\:{a} \\ $$$${we}\:{see} \\ $$$$\Delta=\frac{{br}_{{A}} }{\mathrm{2}}+\frac{{cr}_{{A}} }{\mathrm{2}}−\frac{{ar}_{{A}} }{\mathrm{2}}=\frac{\left({b}+{c}−{a}\right){r}_{{A}} }{\mathrm{2}}=\left({s}−{a}\right){r}_{{A}} \\ $$$$\Rightarrow\left({s}−{a}\right){r}_{{A}} =\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$\Rightarrow{r}_{{A}} =\sqrt{\frac{{s}\left({s}−{b}\right)\left({s}−{c}\right)}{{s}−{a}}} \\ $$$$\Rightarrow{r}_{{A}} =\sqrt{\frac{\mathrm{12}\left(\mathrm{12}−\mathrm{7}\right)\left(\mathrm{12}−\mathrm{8}\right)}{\mathrm{12}−\mathrm{9}}}=\mathrm{4}\sqrt{\mathrm{5}} \\ $$

Commented by mr W last updated on 26/Aug/19

Commented by mr W last updated on 26/Aug/19

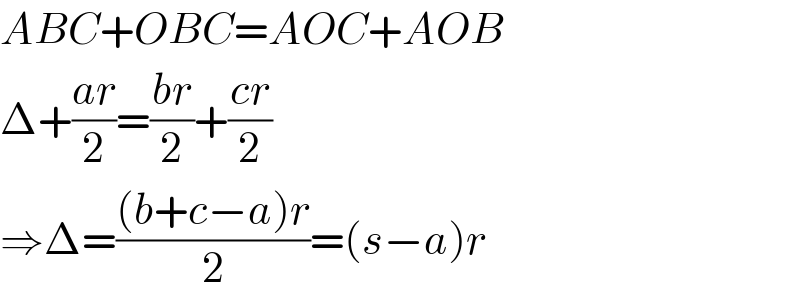
ABC+OBC=AOC+AOB Δ+((ar)/2)=((br)/2)+((cr)/2) ⇒Δ=(((b+c−a)r)/2)=(s−a)r

$${ABC}+{OBC}={AOC}+{AOB} \\ $$$$\Delta+\frac{{ar}}{\mathrm{2}}=\frac{{br}}{\mathrm{2}}+\frac{{cr}}{\mathrm{2}} \\ $$$$\Rightarrow\Delta=\frac{\left({b}+{c}−{a}\right){r}}{\mathrm{2}}=\left({s}−{a}\right){r} \\ $$

Commented by TawaTawa last updated on 26/Aug/19

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by TawaTawa last updated on 26/Aug/19

$$\mathrm{I}\:\mathrm{understand}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by TawaTawa last updated on 26/Aug/19

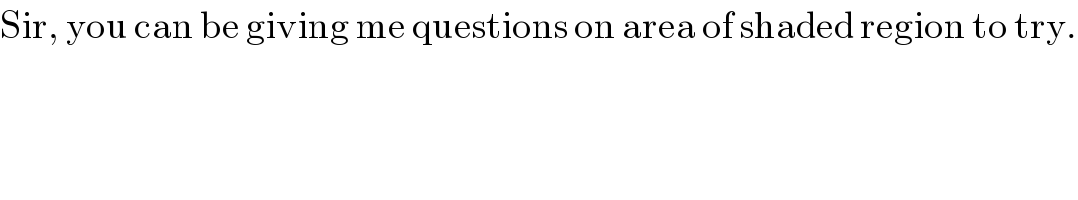
Sir, you can be giving me questions on area of shaded region to try.

$$\mathrm{Sir},\:\mathrm{you}\:\mathrm{can}\:\mathrm{be}\:\mathrm{giving}\:\mathrm{me}\:\mathrm{questions}\:\mathrm{on}\:\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{region}\:\mathrm{to}\:\mathrm{try}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply