Menu Close

Question-67430

Tinku Tara 0 Comments
Pin




Question Number 67430 by TawaTawa last updated on 27/Aug/19
Commented by MJS last updated on 27/Aug/19
coordinate method turn the triangle → CA is the base side length =s s=8+x ⇒ x=s−8 C= (((−(s/2))),(0) ) A= (((s/2)),(0) ) B= ((0),((((√3)s)/2)) ) D= ((((s/2)−3)),(0) ) E= (((5−(s/2))),(0) ) line BD l_1 : y=−(((√3)s)/(s−6))x+(((√3)s)/2) ⇒ tan θ_1 =−(((√3)s)/(s−6)) line BE l_2 : y=(((√3)s)/(s−10))x+(((√3)s)/2) ⇒ tan θ_2 =(((√3)s)/(s−10)) θ_2 −θ_1 =±30° arctan (((√3)s)/(s−10)) +arctan (((√3)s)/(s−6)) =±30° [tan (arctan α +arctan β)=((α+β)/(1−αβ))] −(((√3)(s^2 −8s))/(s^2 +8s−30))=±((√3)/3) ⇒ s=15 ⇒ x=7
$$\mathrm{coordinate}\:\mathrm{method} \\ $$$$\mathrm{turn}\:\mathrm{the}\:\mathrm{triangle}\:\rightarrow\:{CA}\:\mathrm{is}\:\mathrm{the}\:\mathrm{base} \\ $$$$\mathrm{side}\:\mathrm{length}\:={s} \\ $$$${s}=\mathrm{8}+{x}\:\Rightarrow\:{x}={s}−\mathrm{8} \\ $$$${C}=\begin{pmatrix}{−\frac{{s}}{\mathrm{2}}}\\{\mathrm{0}}\end{pmatrix}\:\:{A}=\begin{pmatrix}{\frac{{s}}{\mathrm{2}}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}}\end{pmatrix} \\ $$$${D}=\begin{pmatrix}{\frac{{s}}{\mathrm{2}}−\mathrm{3}}\\{\mathrm{0}}\end{pmatrix}\:\:{E}=\begin{pmatrix}{\mathrm{5}−\frac{{s}}{\mathrm{2}}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{line}\:{BD} \\ $$$${l}_{\mathrm{1}} :\:{y}=−\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{6}}{x}+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\Rightarrow\:\mathrm{tan}\:\theta_{\mathrm{1}} \:=−\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{6}} \\ $$$$\mathrm{line}\:{BE} \\ $$$${l}_{\mathrm{2}} :\:{y}=\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{10}}{x}+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\Rightarrow\:\mathrm{tan}\:\theta_{\mathrm{2}} \:=\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{10}} \\ $$$$\theta_{\mathrm{2}} −\theta_{\mathrm{1}} =\pm\mathrm{30}° \\ $$$$\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{10}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{6}}\:=\pm\mathrm{30}° \\ $$$$\:\:\:\:\:\left[\mathrm{tan}\:\left(\mathrm{arctan}\:\alpha\:+\mathrm{arctan}\:\beta\right)=\frac{\alpha+\beta}{\mathrm{1}−\alpha\beta}\right] \\ $$$$−\frac{\sqrt{\mathrm{3}}\left({s}^{\mathrm{2}} −\mathrm{8}{s}\right)}{{s}^{\mathrm{2}} +\mathrm{8}{s}−\mathrm{30}}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow\:{s}=\mathrm{15} \\ $$$$\Rightarrow\:{x}=\mathrm{7} \\ $$
Commented by TawaTawa last updated on 27/Aug/19
God bless you sir. I appreciate.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by Kunal12588 last updated on 27/Aug/19
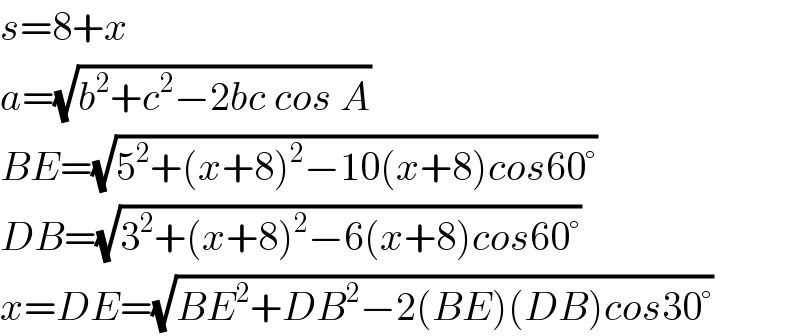
s=8+x a=(√(b^2 +c^2 −2bc cos A)) BE=(√(5^2 +(x+8)^2 −10(x+8)cos60°)) DB=(√(3^2 +(x+8)^2 −6(x+8)cos60°)) x=DE=(√(BE^2 +DB^2 −2(BE)(DB)cos30°))
$${s}=\mathrm{8}+{x} \\ $$$${a}=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:{cos}\:{A}} \\ $$$${BE}=\sqrt{\mathrm{5}^{\mathrm{2}} +\left({x}+\mathrm{8}\right)^{\mathrm{2}} −\mathrm{10}\left({x}+\mathrm{8}\right){cos}\mathrm{60}°} \\ $$$${DB}=\sqrt{\mathrm{3}^{\mathrm{2}} +\left({x}+\mathrm{8}\right)^{\mathrm{2}} −\mathrm{6}\left({x}+\mathrm{8}\right){cos}\mathrm{60}°} \\ $$$${x}={DE}=\sqrt{{BE}^{\mathrm{2}} +{DB}^{\mathrm{2}} −\mathrm{2}\left({BE}\right)\left({DB}\right){cos}\mathrm{30}°} \\ $$
Commented by TawaTawa last updated on 27/Aug/19
God bless you sir. I appreciate.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by mr W last updated on 27/Aug/19
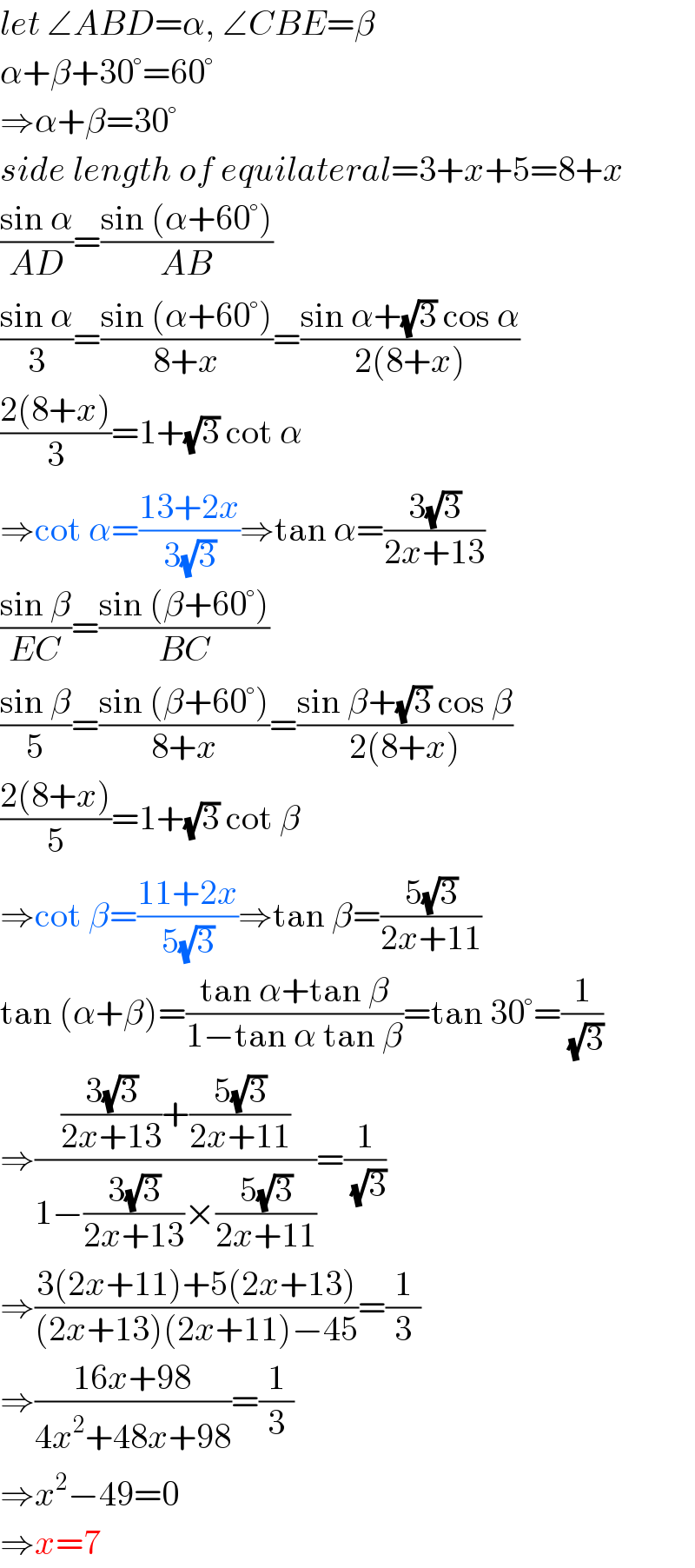
let ∠ABD=α, ∠CBE=β α+β+30°=60° ⇒α+β=30° side length of equilateral=3+x+5=8+x ((sin α)/(AD))=((sin (α+60°))/(AB)) ((sin α)/3)=((sin (α+60°))/(8+x))=((sin α+(√3) cos α)/(2(8+x))) ((2(8+x))/3)=1+(√3) cot α ⇒cot α=((13+2x)/(3(√3)))⇒tan α=((3(√3))/(2x+13)) ((sin β)/(EC))=((sin (β+60°))/(BC)) ((sin β)/5)=((sin (β+60°))/(8+x))=((sin β+(√3) cos β)/(2(8+x))) ((2(8+x))/5)=1+(√3) cot β ⇒cot β=((11+2x)/(5(√3)))⇒tan β=((5(√3))/(2x+11)) tan (α+β)=((tan α+tan β)/(1−tan α tan β))=tan 30°=(1/( (√3))) ⇒((((3(√3))/(2x+13))+((5(√3))/(2x+11)))/(1−((3(√3))/(2x+13))×((5(√3))/(2x+11))))=(1/( (√3))) ⇒((3(2x+11)+5(2x+13))/((2x+13)(2x+11)−45))=(1/3) ⇒((16x+98)/(4x^2 +48x+98))=(1/3) ⇒x^2 −49=0 ⇒x=7
$${let}\:\angle{ABD}=\alpha,\:\angle{CBE}=\beta \\ $$$$\alpha+\beta+\mathrm{30}°=\mathrm{60}° \\ $$$$\Rightarrow\alpha+\beta=\mathrm{30}° \\ $$$${side}\:{length}\:{of}\:{equilateral}=\mathrm{3}+{x}+\mathrm{5}=\mathrm{8}+{x} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{AD}}=\frac{\mathrm{sin}\:\left(\alpha+\mathrm{60}°\right)}{{AB}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{3}}=\frac{\mathrm{sin}\:\left(\alpha+\mathrm{60}°\right)}{\mathrm{8}+{x}}=\frac{\mathrm{sin}\:\alpha+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha}{\mathrm{2}\left(\mathrm{8}+{x}\right)} \\ $$$$\frac{\mathrm{2}\left(\mathrm{8}+{x}\right)}{\mathrm{3}}=\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{cot}\:\alpha \\ $$$$\Rightarrow\mathrm{cot}\:\alpha=\frac{\mathrm{13}+\mathrm{2}{x}}{\mathrm{3}\sqrt{\mathrm{3}}}\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{13}} \\ $$$$\frac{\mathrm{sin}\:\beta}{{EC}}=\frac{\mathrm{sin}\:\left(\beta+\mathrm{60}°\right)}{{BC}} \\ $$$$\frac{\mathrm{sin}\:\beta}{\mathrm{5}}=\frac{\mathrm{sin}\:\left(\beta+\mathrm{60}°\right)}{\mathrm{8}+{x}}=\frac{\mathrm{sin}\:\beta+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\beta}{\mathrm{2}\left(\mathrm{8}+{x}\right)} \\ $$$$\frac{\mathrm{2}\left(\mathrm{8}+{x}\right)}{\mathrm{5}}=\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{cot}\:\beta \\ $$$$\Rightarrow\mathrm{cot}\:\beta=\frac{\mathrm{11}+\mathrm{2}{x}}{\mathrm{5}\sqrt{\mathrm{3}}}\Rightarrow\mathrm{tan}\:\beta=\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{11}} \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}=\mathrm{tan}\:\mathrm{30}°=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\frac{\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{13}}+\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{11}}}{\mathrm{1}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{13}}×\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{11}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\frac{\mathrm{3}\left(\mathrm{2}{x}+\mathrm{11}\right)+\mathrm{5}\left(\mathrm{2}{x}+\mathrm{13}\right)}{\left(\mathrm{2}{x}+\mathrm{13}\right)\left(\mathrm{2}{x}+\mathrm{11}\right)−\mathrm{45}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{16}{x}+\mathrm{98}}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{48}{x}+\mathrm{98}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{49}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{7} \\ $$
Commented by TawaTawa last updated on 27/Aug/19
God bless you sir. I appreciate.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by TawaTawa last updated on 27/Aug/19
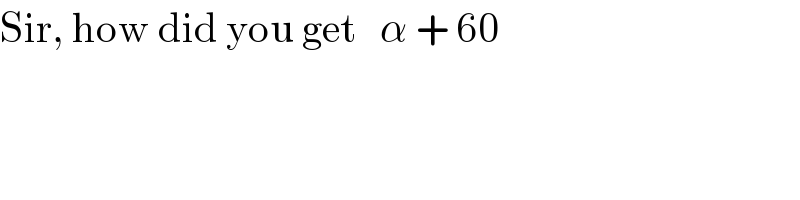
Sir, how did you get α + 60
$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\:\:\alpha\:+\:\mathrm{60} \\ $$
Commented by mr W last updated on 27/Aug/19
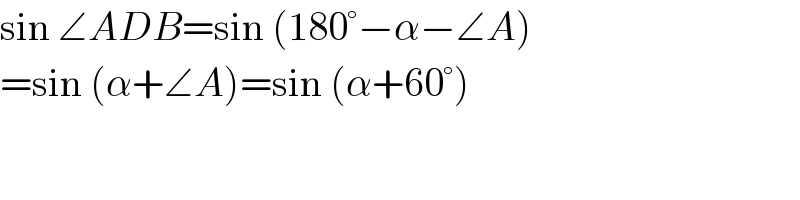
sin ∠ADB=sin (180°−α−∠A) =sin (α+∠A)=sin (α+60°)
$$\mathrm{sin}\:\angle{ADB}=\mathrm{sin}\:\left(\mathrm{180}°−\alpha−\angle{A}\right) \\ $$$$=\mathrm{sin}\:\left(\alpha+\angle{A}\right)=\mathrm{sin}\:\left(\alpha+\mathrm{60}°\right) \\ $$
Commented by TawaTawa last updated on 27/Aug/19
I appreciate your time sir.
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *