Question Number 67454 by Aditya789 last updated on 27/Aug/19

Commented by mathmax by abdo last updated on 27/Aug/19
![here C_r mean C_n ^r we have Σ_(r=0) ^n C_n ^r x^r =(1+x)^n let integrate Σ_(r=0) ^n C_n ^r ∫_0 ^x t^r dt =∫_0 ^x (1+t)^n dt +c ⇒ Σ_(r=0) ^n (C_n ^r /(r+1)) x^(r+1) =(1/(n+1))[ t^(n+1) ]_0 ^x +c = [(1/(n+1))(1+t)^(n+1) ]_0 ^x +c =(1/(n+1)){ (1+x)^(n+1) −1} +c x=0 ⇒c=0 ⇒Σ_(r=0) ^n (C_r /(r+1)) x^(n+1) =(((1+x)^(n+1) −1)/(n+1)) x=1 ⇒ Σ_(r=0) ^n (C_r /(n+1)) =((2^(n+1) −1)/(n+1)) ⇒ C_0 +(C_1 /2) +(C_3 /4) +.....+(C_(n+1) /(n+1)) =((2^(n+1) −1)/(n+1)) .](https://www.tinkutara.com/question/Q67455.png)
$${here}\:{C}_{{r}} \:{mean}\:{C}_{{n}} ^{{r}} \:\:\:\:\:\:{we}\:{have}\:\:\sum_{{r}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:=\left(\mathrm{1}+{x}\right)^{{n}} \:\:{let}\:{integrate} \\ $$$$\overset{{n}} {\sum}_{{r}=\mathrm{0}} \:{C}_{{n}} ^{{r}} \:\int_{\mathrm{0}} ^{{x}} \:{t}^{{r}} \:{dt}\:=\int_{\mathrm{0}} ^{{x}} \left(\mathrm{1}+{t}\right)^{{n}} {dt}\:+{c}\:\Rightarrow \\ $$$$\sum_{{r}=\mathrm{0}} ^{{n}} \:\:\frac{{C}_{{n}} ^{{r}} }{{r}+\mathrm{1}}\:{x}^{{r}+\mathrm{1}} \:\:=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left[\:{t}^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{{x}} \:+{c}\:=\:\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\mathrm{1}+{t}\right)^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{{x}} \:+{c} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left\{\:\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\mathrm{1}\right\}\:+{c} \\ $$$${x}=\mathrm{0}\:\Rightarrow{c}=\mathrm{0}\:\:\Rightarrow\sum_{{r}=\mathrm{0}} ^{{n}} \:\:\:\frac{{C}_{{r}} }{{r}+\mathrm{1}}\:{x}^{{n}+\mathrm{1}} \:=\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${x}=\mathrm{1}\:\Rightarrow\:\sum_{{r}=\mathrm{0}} ^{{n}} \:\frac{{C}_{{r}} }{{n}+\mathrm{1}}\:=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow \\ $$$${C}_{\mathrm{0}} \:\:+\frac{{C}_{\mathrm{1}} }{\mathrm{2}}\:+\frac{{C}_{\mathrm{3}} }{\mathrm{4}}\:+…..+\frac{{C}_{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}\:\:\:. \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19
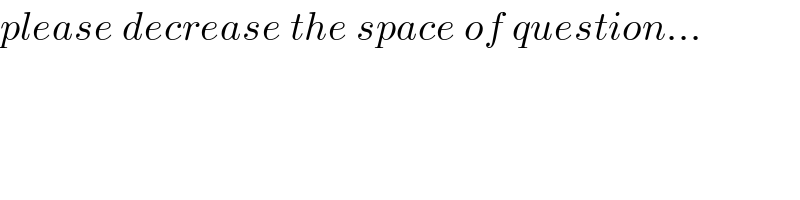
$${please}\:{decrease}\:{the}\:{space}\:{of}\:{question}… \\ $$
