Question Number 6748 by Leila Akram last updated on 21/Jul/16

Answered by Yozzii last updated on 21/Jul/16
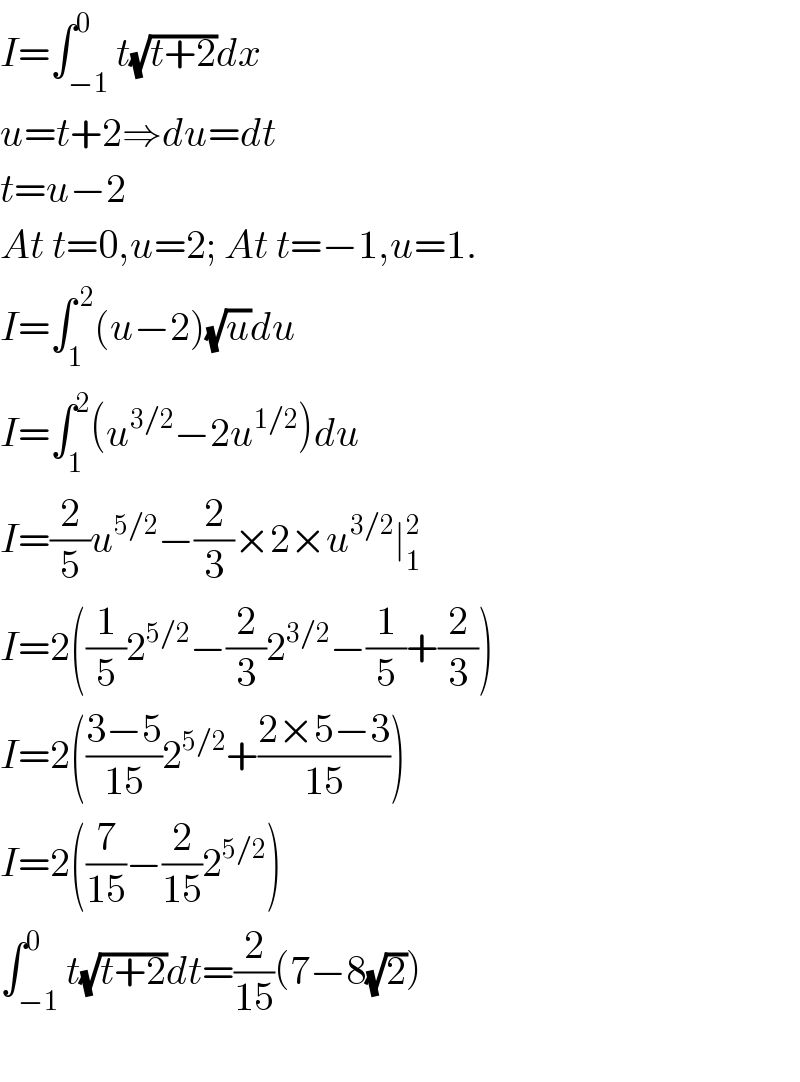
$${I}=\int_{−\mathrm{1}} ^{\mathrm{0}} {t}\sqrt{{t}+\mathrm{2}}{dx} \\ $$$${u}={t}+\mathrm{2}\Rightarrow{du}={dt} \\ $$$${t}={u}−\mathrm{2} \\ $$$${At}\:{t}=\mathrm{0},{u}=\mathrm{2};\:{At}\:{t}=−\mathrm{1},{u}=\mathrm{1}. \\ $$$${I}=\int_{\mathrm{1}} ^{\:\mathrm{2}} \left({u}−\mathrm{2}\right)\sqrt{{u}}{du} \\ $$$${I}=\int_{\mathrm{1}} ^{\mathrm{2}} \left({u}^{\mathrm{3}/\mathrm{2}} −\mathrm{2}{u}^{\mathrm{1}/\mathrm{2}} \right){du} \\ $$$${I}=\frac{\mathrm{2}}{\mathrm{5}}{u}^{\mathrm{5}/\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{2}×{u}^{\mathrm{3}/\mathrm{2}} \mid_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${I}=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{5}}\mathrm{2}^{\mathrm{5}/\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\mathrm{2}^{\mathrm{3}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$${I}=\mathrm{2}\left(\frac{\mathrm{3}−\mathrm{5}}{\mathrm{15}}\mathrm{2}^{\mathrm{5}/\mathrm{2}} +\frac{\mathrm{2}×\mathrm{5}−\mathrm{3}}{\mathrm{15}}\right) \\ $$$${I}=\mathrm{2}\left(\frac{\mathrm{7}}{\mathrm{15}}−\frac{\mathrm{2}}{\mathrm{15}}\mathrm{2}^{\mathrm{5}/\mathrm{2}} \right) \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{0}} {t}\sqrt{{t}+\mathrm{2}}{dt}=\frac{\mathrm{2}}{\mathrm{15}}\left(\mathrm{7}−\mathrm{8}\sqrt{\mathrm{2}}\right) \\ $$$$ \\ $$
