Question Number 67514 by mr W last updated on 28/Aug/19
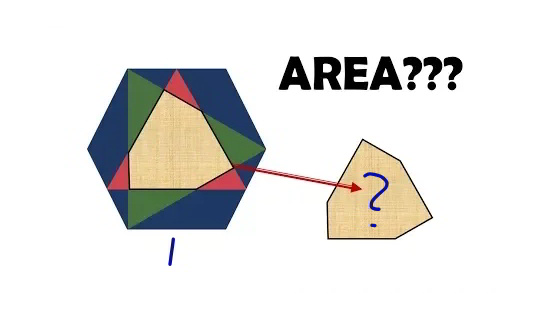
Commented by mr W last updated on 28/Aug/19
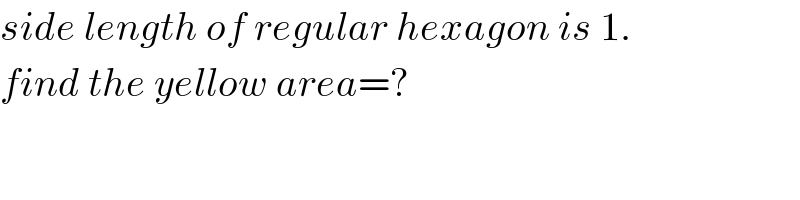
$${side}\:{length}\:{of}\:{regular}\:{hexagon}\:{is}\:\mathrm{1}. \\ $$$${find}\:{the}\:{yellow}\:{area}=? \\ $$
Answered by mr W last updated on 29/Aug/19
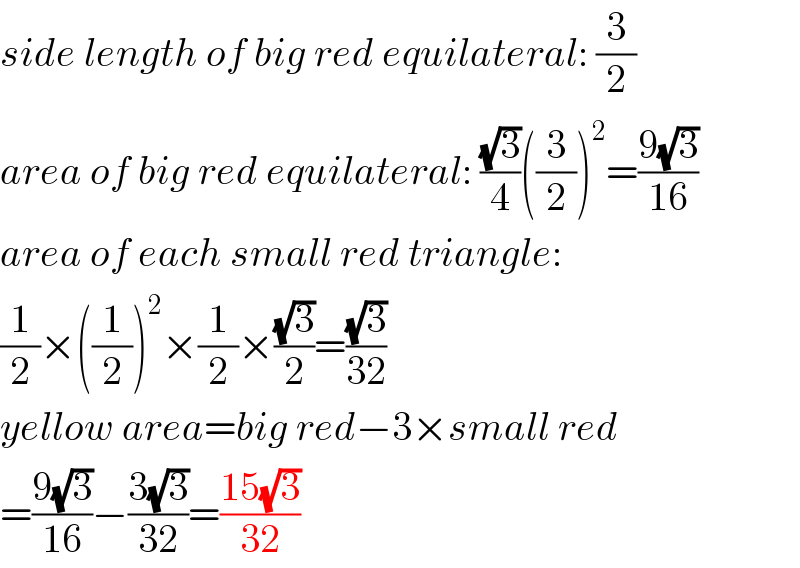
$${side}\:{length}\:{of}\:{big}\:{red}\:{equilateral}:\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${area}\:{of}\:{big}\:{red}\:{equilateral}:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{16}} \\ $$$${area}\:{of}\:{each}\:{small}\:{red}\:{triangle}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{32}} \\ $$$${yellow}\:{area}={big}\:{red}−\mathrm{3}×{small}\:{red} \\ $$$$=\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{16}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}=\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{32}} \\ $$
