Menu Close

Question-67516

Tinku Tara 0 Comments
Pin




Question Number 67516 by LPM last updated on 28/Aug/19
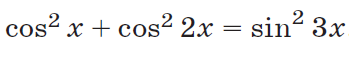
Commented by Prithwish sen last updated on 28/Aug/19
cos^2 x +(2cos^2 x−1)^2 = 1−cos^2 3x Simplyfying we get, 2cos^2 x(4cos^4 x−10cos^2 x+3)=0 ⇒cos^2 x = 0 and cos^2 x=((10±(√(52)))/8) ∴ x=(2n−1)(π/2) and x = Cos^(−1) [((√(5±(√(13))))/2)] please check.
$$\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:+\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} =\:\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{3x} \\ $$$$\mathrm{Simplyfying}\:\mathrm{we}\:\mathrm{get}, \\ $$$$\mathrm{2cos}^{\mathrm{2}} \mathrm{x}\left(\mathrm{4cos}^{\mathrm{4}} \mathrm{x}−\mathrm{10cos}^{\mathrm{2}} \mathrm{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{0}\:\:\:\mathrm{and}\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}=\frac{\mathrm{10}\pm\sqrt{\mathrm{52}}}{\mathrm{8}} \\ $$$$\therefore\:\mathrm{x}=\left(\mathrm{2n}−\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{x}\:=\:\mathrm{Cos}^{−\mathrm{1}} \left[\frac{\sqrt{\mathrm{5}\pm\sqrt{\mathrm{13}}}}{\mathrm{2}}\right] \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by mathmax by abdo last updated on 19/Sep/19
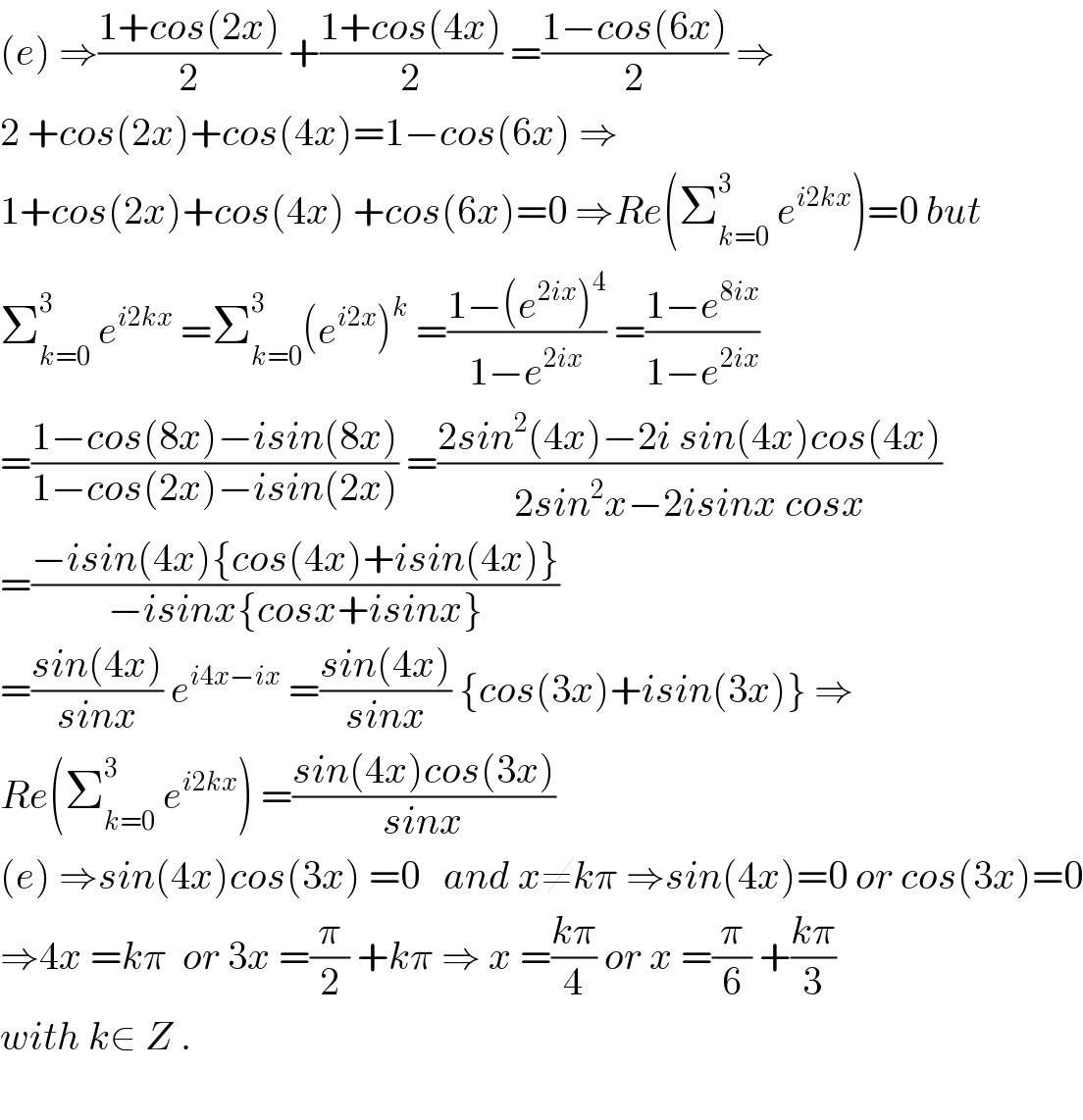
(e) ⇒((1+cos(2x))/2) +((1+cos(4x))/2) =((1−cos(6x))/2) ⇒ 2 +cos(2x)+cos(4x)=1−cos(6x) ⇒ 1+cos(2x)+cos(4x) +cos(6x)=0 ⇒Re(Σ_(k=0) ^3 e^(i2kx) )=0 but Σ_(k=0) ^3 e^(i2kx) =Σ_(k=0) ^3 (e^(i2x) )^k =((1−(e^(2ix) )^4 )/(1−e^(2ix) )) =((1−e^(8ix) )/(1−e^(2ix) )) =((1−cos(8x)−isin(8x))/(1−cos(2x)−isin(2x))) =((2sin^2 (4x)−2i sin(4x)cos(4x))/(2sin^2 x−2isinx cosx)) =((−isin(4x){cos(4x)+isin(4x)})/(−isinx{cosx+isinx})) =((sin(4x))/(sinx)) e^(i4x−ix) =((sin(4x))/(sinx)) {cos(3x)+isin(3x)} ⇒ Re(Σ_(k=0) ^3 e^(i2kx) ) =((sin(4x)cos(3x))/(sinx)) (e) ⇒sin(4x)cos(3x) =0 and x≠kπ ⇒sin(4x)=0 or cos(3x)=0 ⇒4x =kπ or 3x =(π/2) +kπ ⇒ x =((kπ)/4) or x =(π/6) +((kπ)/3) with k∈ Z .
$$\left({e}\right)\:\Rightarrow\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\:=\frac{\mathrm{1}−{cos}\left(\mathrm{6}{x}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{2}\:+{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{4}{x}\right)=\mathrm{1}−{cos}\left(\mathrm{6}{x}\right)\:\Rightarrow \\ $$$$\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{4}{x}\right)\:+{cos}\left(\mathrm{6}{x}\right)=\mathrm{0}\:\Rightarrow{Re}\left(\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \:{e}^{{i}\mathrm{2}{kx}} \right)=\mathrm{0}\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \:{e}^{{i}\mathrm{2}{kx}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \left({e}^{{i}\mathrm{2}{x}} \right)^{{k}} \:=\frac{\mathrm{1}−\left({e}^{\mathrm{2}{ix}} \right)^{\mathrm{4}} }{\mathrm{1}−{e}^{\mathrm{2}{ix}} }\:=\frac{\mathrm{1}−{e}^{\mathrm{8}{ix}} }{\mathrm{1}−{e}^{\mathrm{2}{ix}} } \\ $$$$=\frac{\mathrm{1}−{cos}\left(\mathrm{8}{x}\right)−{isin}\left(\mathrm{8}{x}\right)}{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)−{isin}\left(\mathrm{2}{x}\right)}\:=\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\mathrm{4}{x}\right)−\mathrm{2}{i}\:{sin}\left(\mathrm{4}{x}\right){cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}{sin}^{\mathrm{2}} {x}−\mathrm{2}{isinx}\:{cosx}} \\ $$$$=\frac{−{isin}\left(\mathrm{4}{x}\right)\left\{{cos}\left(\mathrm{4}{x}\right)+{isin}\left(\mathrm{4}{x}\right)\right\}}{−{isinx}\left\{{cosx}+{isinx}\right\}} \\ $$$$=\frac{{sin}\left(\mathrm{4}{x}\right)}{{sinx}}\:{e}^{{i}\mathrm{4}{x}−{ix}} \:=\frac{{sin}\left(\mathrm{4}{x}\right)}{{sinx}}\:\left\{{cos}\left(\mathrm{3}{x}\right)+{isin}\left(\mathrm{3}{x}\right)\right\}\:\Rightarrow \\ $$$${Re}\left(\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \:{e}^{{i}\mathrm{2}{kx}} \right)\:=\frac{{sin}\left(\mathrm{4}{x}\right){cos}\left(\mathrm{3}{x}\right)}{{sinx}} \\ $$$$\left({e}\right)\:\Rightarrow{sin}\left(\mathrm{4}{x}\right){cos}\left(\mathrm{3}{x}\right)\:=\mathrm{0}\:\:\:{and}\:{x}\neq{k}\pi\:\Rightarrow{sin}\left(\mathrm{4}{x}\right)=\mathrm{0}\:{or}\:{cos}\left(\mathrm{3}{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}{x}\:={k}\pi\:\:{or}\:\mathrm{3}{x}\:=\frac{\pi}{\mathrm{2}}\:+{k}\pi\:\Rightarrow\:{x}\:=\frac{{k}\pi}{\mathrm{4}}\:{or}\:{x}\:=\frac{\pi}{\mathrm{6}}\:+\frac{{k}\pi}{\mathrm{3}} \\ $$$${with}\:{k}\in\:{Z}\:. \\ $$$$ \\ $$
Answered by MJS last updated on 18/Sep/19
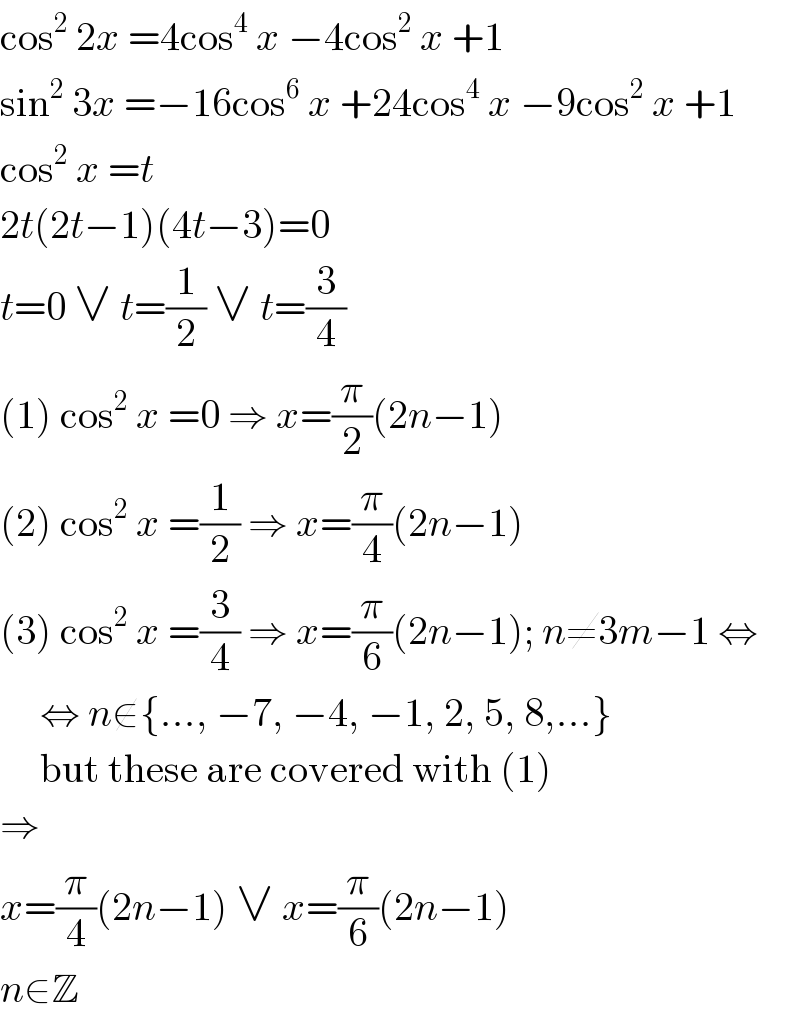
cos^2 2x =4cos^4 x −4cos^2 x +1 sin^2 3x =−16cos^6 x +24cos^4 x −9cos^2 x +1 cos^2 x =t 2t(2t−1)(4t−3)=0 t=0 ∨ t=(1/2) ∨ t=(3/4) (1) cos^2 x =0 ⇒ x=(π/2)(2n−1) (2) cos^2 x =(1/2) ⇒ x=(π/4)(2n−1) (3) cos^2 x =(3/4) ⇒ x=(π/6)(2n−1); n≠3m−1 ⇔ ⇔ n∉{..., −7, −4, −1, 2, 5, 8,...} but these are covered with (1) ⇒ x=(π/4)(2n−1) ∨ x=(π/6)(2n−1) n∈Z
$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}\:=\mathrm{4cos}^{\mathrm{4}} \:{x}\:−\mathrm{4cos}^{\mathrm{2}} \:{x}\:+\mathrm{1} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{3}{x}\:=−\mathrm{16cos}^{\mathrm{6}} \:{x}\:+\mathrm{24cos}^{\mathrm{4}} \:{x}\:−\mathrm{9cos}^{\mathrm{2}} \:{x}\:+\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:={t} \\ $$$$\mathrm{2}{t}\left(\mathrm{2}{t}−\mathrm{1}\right)\left(\mathrm{4}{t}−\mathrm{3}\right)=\mathrm{0} \\ $$$${t}=\mathrm{0}\:\vee\:{t}=\frac{\mathrm{1}}{\mathrm{2}}\:\vee\:{t}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{cos}^{\mathrm{2}} \:{x}\:=\mathrm{0}\:\Rightarrow\:{x}=\frac{\pi}{\mathrm{2}}\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{cos}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{x}=\frac{\pi}{\mathrm{4}}\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$$\left(\mathrm{3}\right)\:\mathrm{cos}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow\:{x}=\frac{\pi}{\mathrm{6}}\left(\mathrm{2}{n}−\mathrm{1}\right);\:{n}\neq\mathrm{3}{m}−\mathrm{1}\:\Leftrightarrow \\ $$$$\:\:\:\:\:\Leftrightarrow\:{n}\notin\left\{…,\:−\mathrm{7},\:−\mathrm{4},\:−\mathrm{1},\:\mathrm{2},\:\mathrm{5},\:\mathrm{8},…\right\} \\ $$$$\:\:\:\:\:\mathrm{but}\:\mathrm{these}\:\mathrm{are}\:\mathrm{covered}\:\mathrm{with}\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow \\ $$$${x}=\frac{\pi}{\mathrm{4}}\left(\mathrm{2}{n}−\mathrm{1}\right)\:\vee\:{x}=\frac{\pi}{\mathrm{6}}\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$${n}\in\mathbb{Z} \\ $$
Commented by Prithwish sen last updated on 28/Aug/19
thank you sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 28/Aug/19
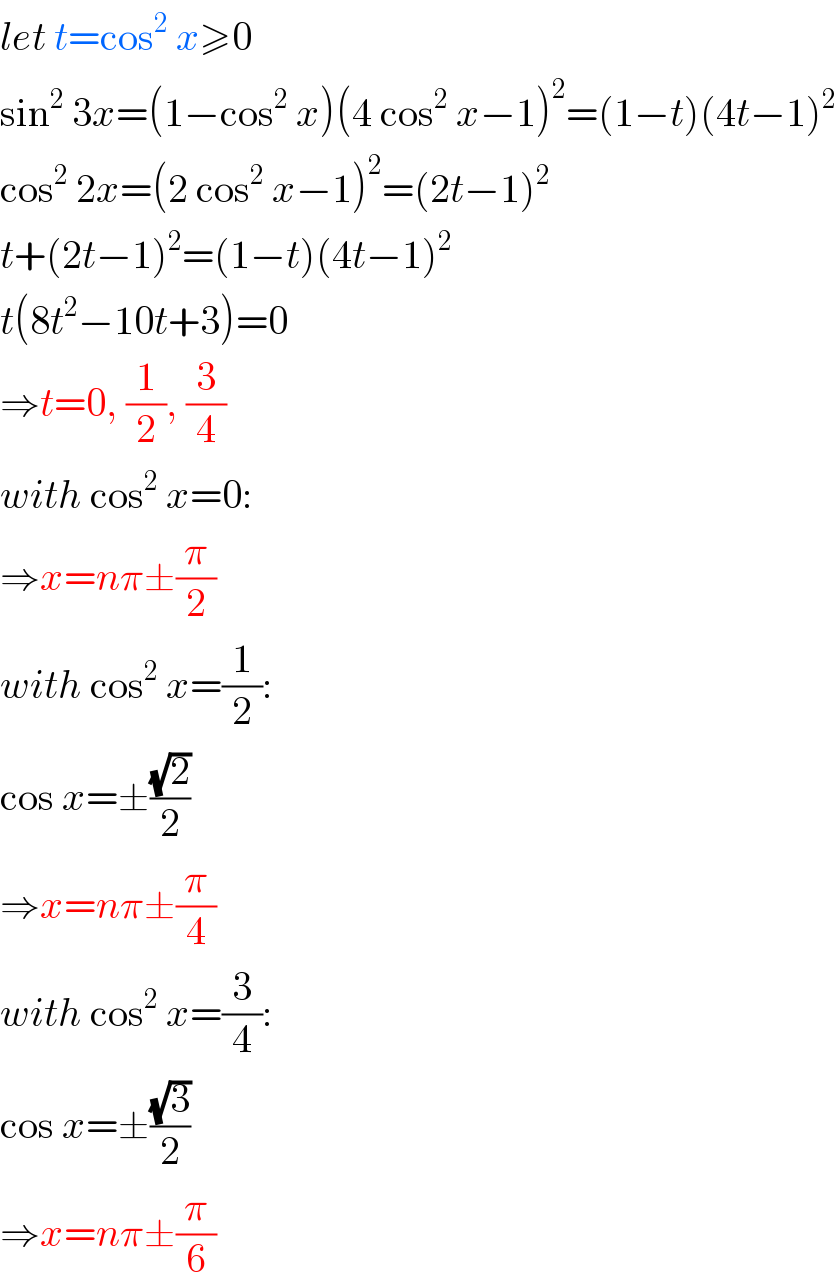
let t=cos^2 x≥0 sin^2 3x=(1−cos^2 x)(4 cos^2 x−1)^2 =(1−t)(4t−1)^2 cos^2 2x=(2 cos^2 x−1)^2 =(2t−1)^2 t+(2t−1)^2 =(1−t)(4t−1)^2 t(8t^2 −10t+3)=0 ⇒t=0, (1/2), (3/4) with cos^2 x=0: ⇒x=nπ±(π/2) with cos^2 x=(1/2): cos x=±((√2)/2) ⇒x=nπ±(π/4) with cos^2 x=(3/4): cos x=±((√3)/2) ⇒x=nπ±(π/6)
$${let}\:{t}=\mathrm{cos}^{\mathrm{2}} \:{x}\geqslant\mathrm{0} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{3}{x}=\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}\right)\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:{x}−\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)\left(\mathrm{4}{t}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}=\left(\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:{x}−\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${t}+\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)\left(\mathrm{4}{t}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${t}\left(\mathrm{8}{t}^{\mathrm{2}} −\mathrm{10}{t}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{0},\:\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${with}\:\mathrm{cos}^{\mathrm{2}} \:{x}=\mathrm{0}: \\ $$$$\Rightarrow{x}={n}\pi\pm\frac{\pi}{\mathrm{2}} \\ $$$${with}\:\mathrm{cos}^{\mathrm{2}} \:{x}=\frac{\mathrm{1}}{\mathrm{2}}: \\ $$$$\mathrm{cos}\:{x}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}={n}\pi\pm\frac{\pi}{\mathrm{4}} \\ $$$${with}\:\mathrm{cos}^{\mathrm{2}} \:{x}=\frac{\mathrm{3}}{\mathrm{4}}: \\ $$$$\mathrm{cos}\:{x}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}={n}\pi\pm\frac{\pi}{\mathrm{6}} \\ $$
Commented by Prithwish sen last updated on 28/Aug/19
thank you sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by LPM last updated on 29/Aug/19
goood
$$\mathrm{goood} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *