Question-67535

Question Number 67535 by mr W last updated on 28/Aug/19

Commented by mr W last updated on 28/Aug/19

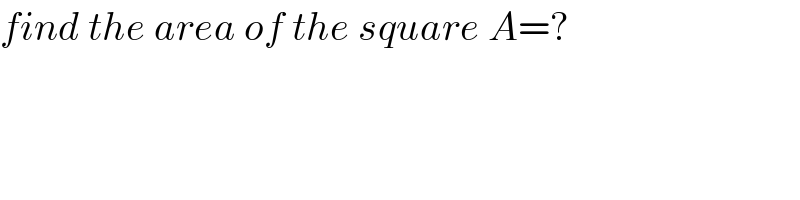
$${find}\:{the}\:{area}\:{of}\:{the}\:{square}\:{A}=? \\ $$

Commented by Prithwish sen last updated on 28/Aug/19

$$\boldsymbol{\mathrm{Area}}\:=\:\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\mathrm{2}} \\ $$

Commented by petrochengula last updated on 28/Aug/19

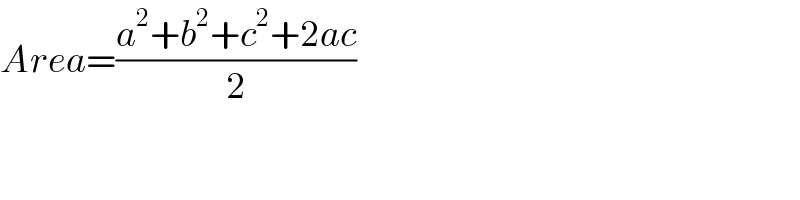
$${Area}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}{ac}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 28/Aug/19

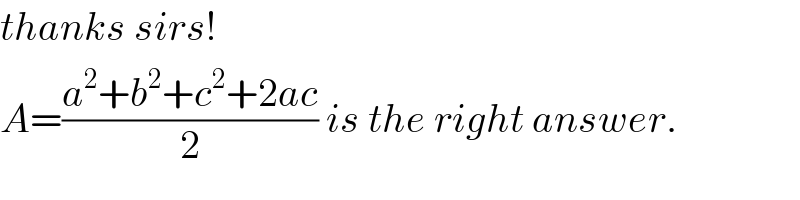
thanks sirs! A=((a^2 +b^2 +c^2 +2ac)/2) is the right answer.

$${thanks}\:{sirs}! \\ $$$${A}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}{ac}}{\mathrm{2}}\:{is}\:{the}\:{right}\:{answer}. \\ $$

Commented by Prithwish sen last updated on 28/Aug/19

Sorry it will be (a+c)^2 . Thank you sir

$$\mathrm{Sorry}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be}\:\left(\mathrm{a}+\mathrm{c}\right)^{\mathrm{2}} \:.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 28/Aug/19

Commented by mr W last updated on 28/Aug/19

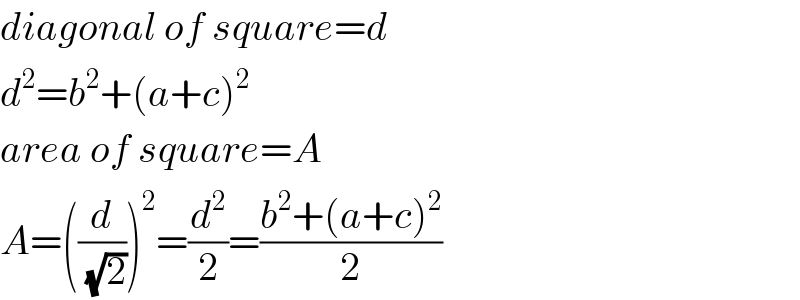
diagonal of square=d d^2 =b^2 +(a+c)^2 area of square=A A=((d/( (√2))))^2 =(d^2 /2)=((b^2 +(a+c)^2 )/2)

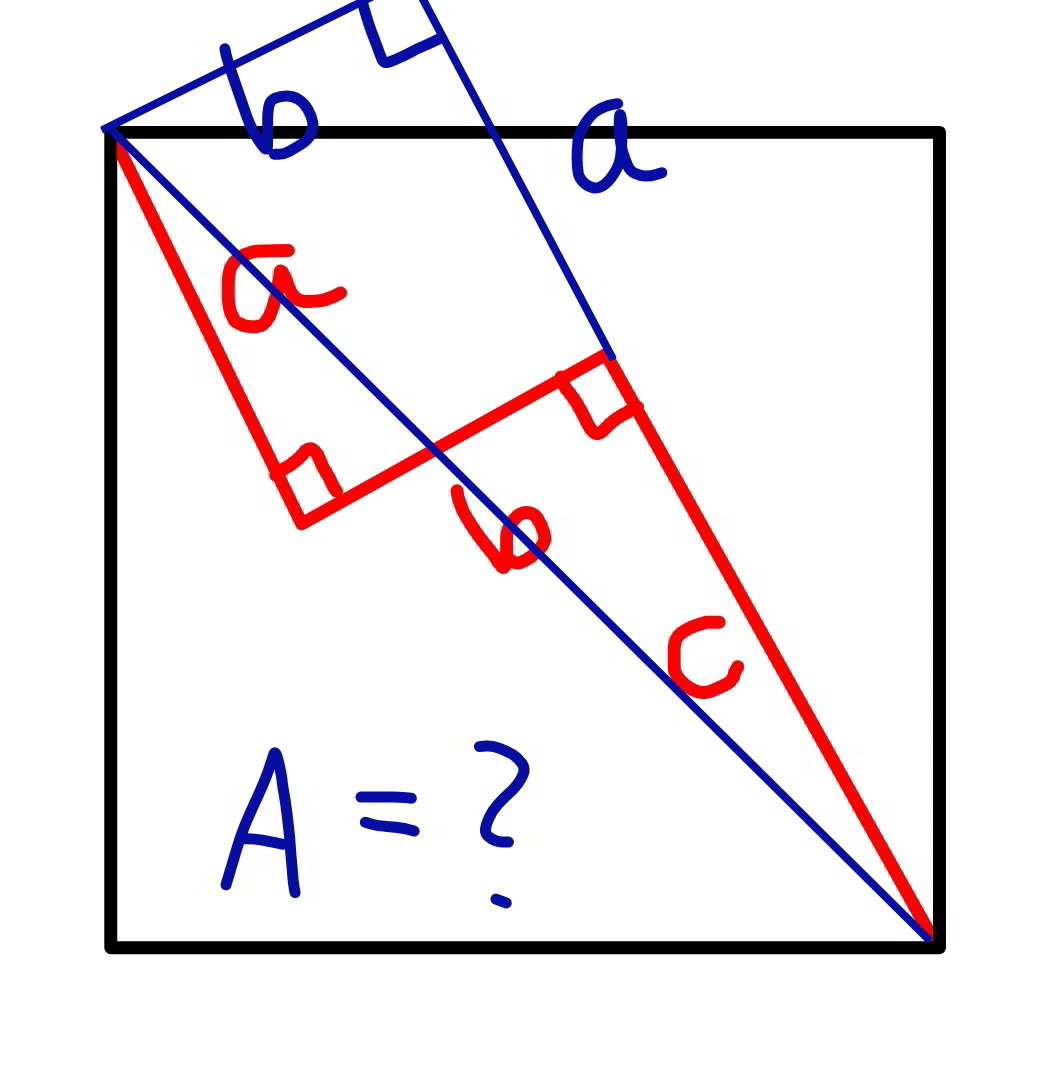
$${diagonal}\:{of}\:{square}={d} \\ $$$${d}^{\mathrm{2}} ={b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} \\ $$$${area}\:{of}\:{square}={A} \\ $$$${A}=\left(\frac{{d}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\frac{{d}^{\mathrm{2}} }{\mathrm{2}}=\frac{{b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$

Commented by Prithwish sen last updated on 28/Aug/19

$$\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}. \\ $$

Commented by TawaTawa last updated on 28/Aug/19

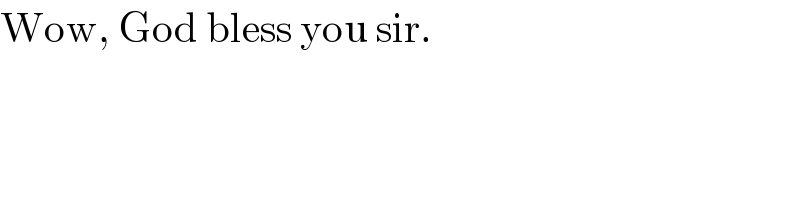
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by Rasheed.Sindhi last updated on 28/Aug/19

The red line segments (having lengths a,b & c) divide the square into two parts.Find out the area of any part.

$${The}\:{red}\:{line}\:{segments}\:\left({having}\:{lengths}\right. \\ $$$$\left.{a},{b}\:\&\:{c}\right)\:{divide}\:{the}\:{square}\:{into}\:{two} \\ $$$${parts}.{Find}\:{out}\:{the}\:{area}\:{of}\:{any}\:{part}. \\ $$

Commented by mr W last updated on 28/Aug/19

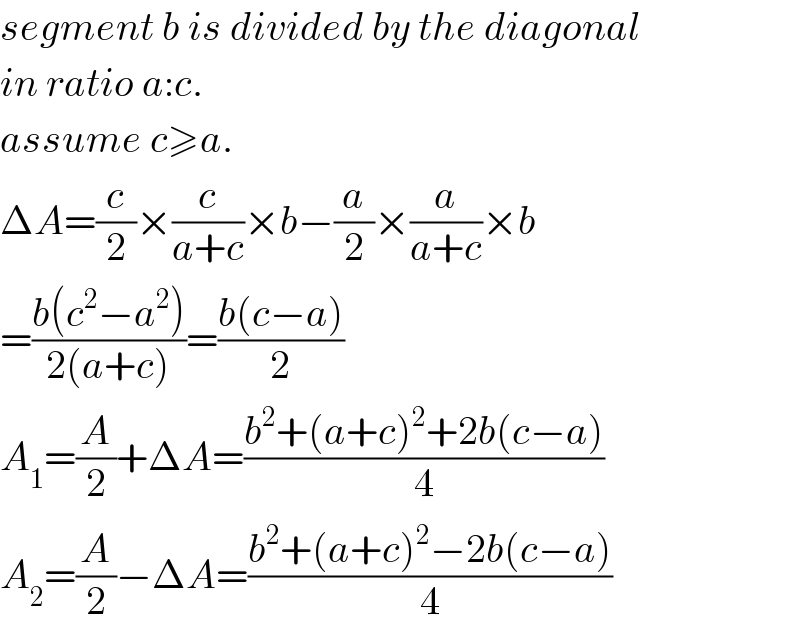
segment b is divided by the diagonal in ratio a:c. assume c≥a. ΔA=(c/2)×(c/(a+c))×b−(a/2)×(a/(a+c))×b =((b(c^2 −a^2 ))/(2(a+c)))=((b(c−a))/2) A_1 =(A/2)+ΔA=((b^2 +(a+c)^2 +2b(c−a))/4) A_2 =(A/2)−ΔA=((b^2 +(a+c)^2 −2b(c−a))/4)

$${segment}\:{b}\:{is}\:{divided}\:{by}\:{the}\:{diagonal} \\ $$$${in}\:{ratio}\:{a}:{c}. \\ $$$${assume}\:{c}\geqslant{a}. \\ $$$$\Delta{A}=\frac{{c}}{\mathrm{2}}×\frac{{c}}{{a}+{c}}×{b}−\frac{{a}}{\mathrm{2}}×\frac{{a}}{{a}+{c}}×{b} \\ $$$$=\frac{{b}\left({c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{\mathrm{2}\left({a}+{c}\right)}=\frac{{b}\left({c}−{a}\right)}{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} =\frac{{A}}{\mathrm{2}}+\Delta{A}=\frac{{b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} +\mathrm{2}{b}\left({c}−{a}\right)}{\mathrm{4}} \\ $$$${A}_{\mathrm{2}} =\frac{{A}}{\mathrm{2}}−\Delta{A}=\frac{{b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} −\mathrm{2}{b}\left({c}−{a}\right)}{\mathrm{4}} \\ $$

Commented by Rasheed.Sindhi last updated on 29/Aug/19

سائين توھان جي مھرباني!Thanks s¡r

Commented by mr W last updated on 30/Aug/19

$${Tawhaan}\:{jee}\:{mehrbaani}! \\ $$

Commented by Rasheed.Sindhi last updated on 30/Aug/19

You have written exactly correct in roman alphabet!

$$\mathrm{You}\:\mathrm{have}\:\mathrm{written}\:\boldsymbol{\mathrm{exactly}}\:\mathrm{correct} \\ $$$$\mathrm{in}\:\mathrm{roman}\:\mathrm{alphabet}! \\ $$

Commented by Rasheed.Sindhi last updated on 30/Aug/19

Sir, ich fühle mich mit Ihnen freundlicher als jeder andere Forum-Freund von mir.

Commented by mr W last updated on 30/Aug/19

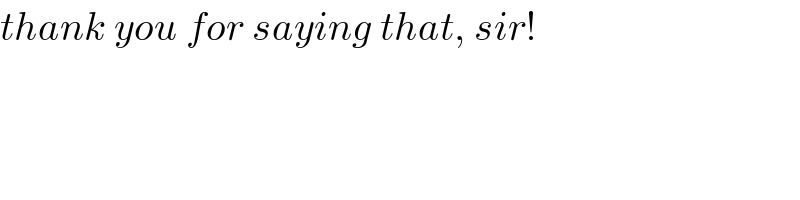
$${thank}\:{you}\:{for}\:{saying}\:{that},\:{sir}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply