Question Number 67617 by aliesam last updated on 29/Aug/19
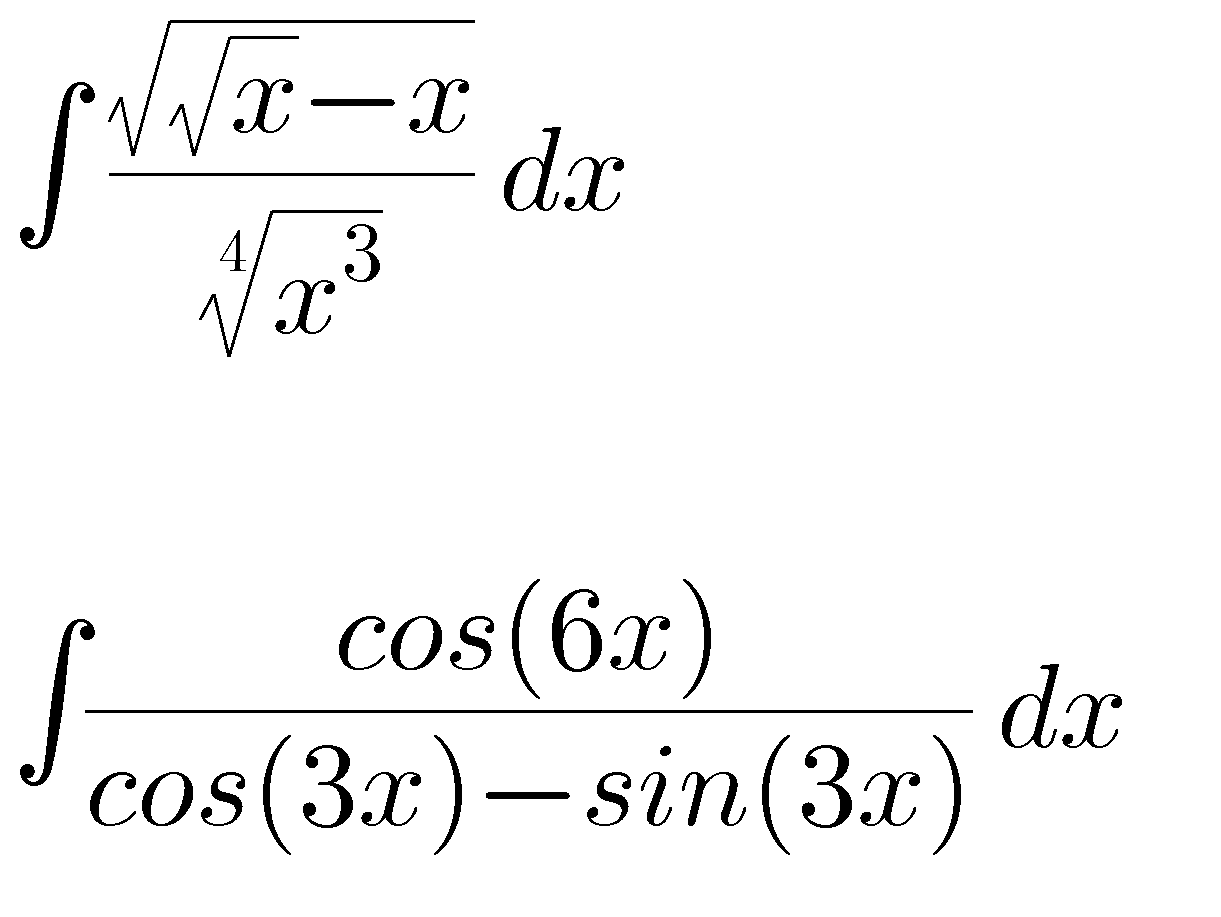
Commented by kaivan.ahmadi last updated on 29/Aug/19
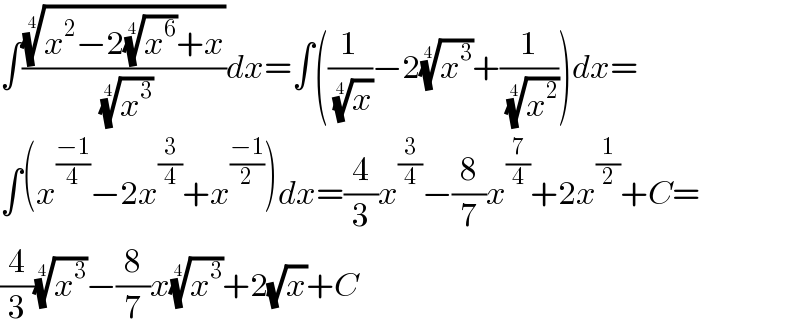
$$\int\frac{\sqrt[{\mathrm{4}}]{{x}^{\mathrm{2}} −\mathrm{2}\sqrt[{\mathrm{4}}]{{x}^{\mathrm{6}} }+{x}}}{\:\sqrt[{\mathrm{4}}]{{x}^{\mathrm{3}} }}{dx}=\int\left(\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{{x}}}−\mathrm{2}\sqrt[{\mathrm{4}}]{{x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{{x}^{\mathrm{2}} }}\right){dx}= \\ $$$$\int\left({x}^{\frac{−\mathrm{1}}{\mathrm{4}}} −\mathrm{2}{x}^{\frac{\mathrm{3}}{\mathrm{4}}} +{x}^{\frac{−\mathrm{1}}{\mathrm{2}}} \right){dx}=\frac{\mathrm{4}}{\mathrm{3}}{x}^{\frac{\mathrm{3}}{\mathrm{4}}} −\frac{\mathrm{8}}{\mathrm{7}}{x}^{\frac{\mathrm{7}}{\mathrm{4}}} +\mathrm{2}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +{C}= \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\sqrt[{\mathrm{4}}]{{x}^{\mathrm{3}} }−\frac{\mathrm{8}}{\mathrm{7}}{x}\sqrt[{\mathrm{4}}]{{x}^{\mathrm{3}} }+\mathrm{2}\sqrt{{x}}+{C} \\ $$
Commented by mathmax by abdo last updated on 29/Aug/19
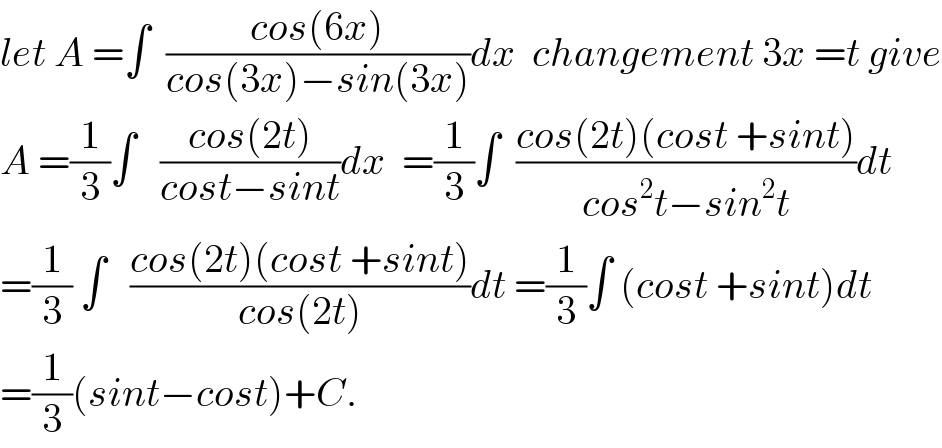
$${let}\:{A}\:=\int\:\:\frac{{cos}\left(\mathrm{6}{x}\right)}{{cos}\left(\mathrm{3}{x}\right)−{sin}\left(\mathrm{3}{x}\right)}{dx}\:\:{changement}\:\mathrm{3}{x}\:={t}\:{give} \\ $$$${A}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\:\:\:\frac{{cos}\left(\mathrm{2}{t}\right)}{{cost}−{sint}}{dx}\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int\:\:\frac{{cos}\left(\mathrm{2}{t}\right)\left({cost}\:+{sint}\right)}{{cos}^{\mathrm{2}} {t}−{sin}^{\mathrm{2}} {t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\:\:\frac{{cos}\left(\mathrm{2}{t}\right)\left({cost}\:+{sint}\right)}{{cos}\left(\mathrm{2}{t}\right)}{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\:\left({cost}\:+{sint}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({sint}−{cost}\right)+{C}. \\ $$
