Question Number 67655 by ajfour last updated on 29/Aug/19
Commented by ajfour last updated on 29/Aug/19

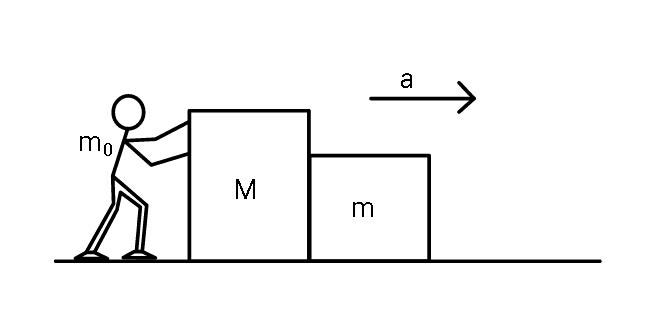
$${If}\:{the}\:{man}\:{can}\:{provide}\:{a}\:{maximum} \\ $$$${acceleration}\:\boldsymbol{{a}}\:{to}\:{the}\:{boxes}\:{while} \\ $$$${he}\:{runs}\:{along},\:{find}\:{the}\:{friction} \\ $$$${coefficient}\:{of}\:{his}\:{shoes}\:{with} \\ $$$${ground}.\:\left({Assume}\:{the}\:{ground}\:{has}\right. \\ $$$${the}\:{same}\:{friction}\:{coefficient} \\ $$$$\left({static}\:{or}\:{kinetic}\:{with}\:{the}\:{boxes}\right. \\ $$$$\left.{and}\:{the}\:{man}'{s}\:{shoes}\right). \\ $$
Commented by mr W last updated on 30/Aug/19
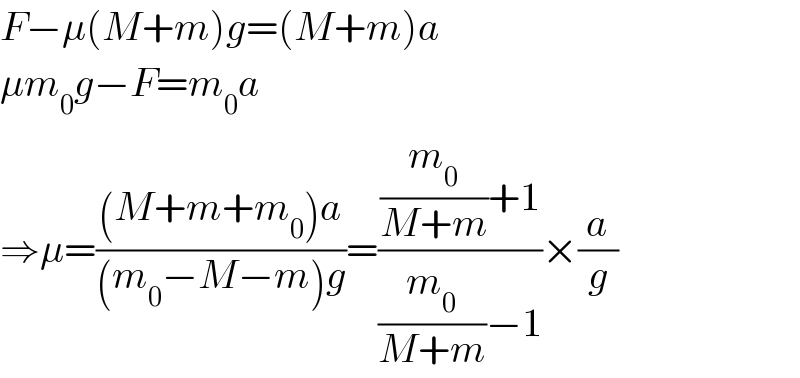
$${F}−\mu\left({M}+{m}\right){g}=\left({M}+{m}\right){a} \\ $$$$\mu{m}_{\mathrm{0}} {g}−{F}={m}_{\mathrm{0}} {a} \\ $$$$\Rightarrow\mu=\frac{\left({M}+{m}+{m}_{\mathrm{0}} \right){a}}{\left({m}_{\mathrm{0}} −{M}−{m}\right){g}}=\frac{\frac{{m}_{\mathrm{0}} }{{M}+{m}}+\mathrm{1}}{\frac{{m}_{\mathrm{0}} }{{M}+{m}}−\mathrm{1}}×\frac{{a}}{{g}} \\ $$
Commented by ajfour last updated on 29/Aug/19
$${Very}\:{precise},\:{and}\:{correct},\:{Sir}. \\ $$$${thanks}! \\ $$
