Question Number 67719 by aliesam last updated on 30/Aug/19
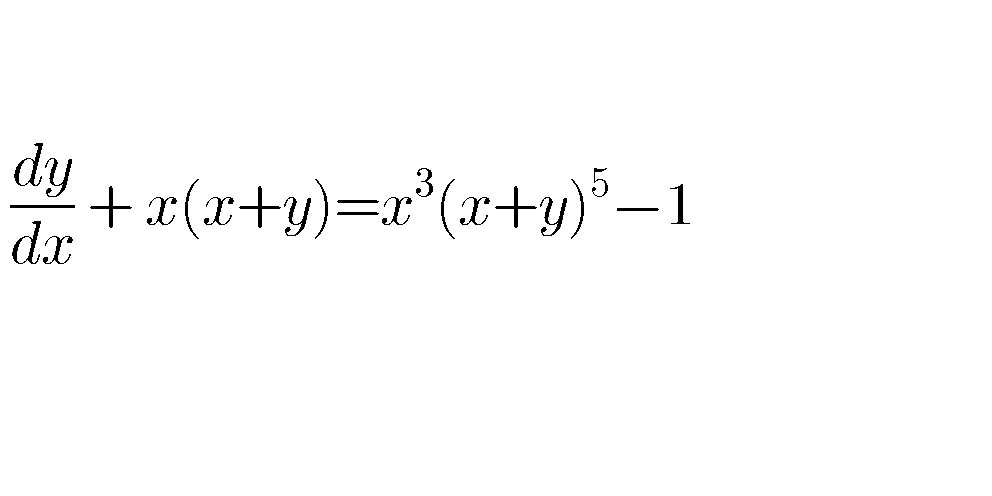
Answered by mind is power last updated on 30/Aug/19
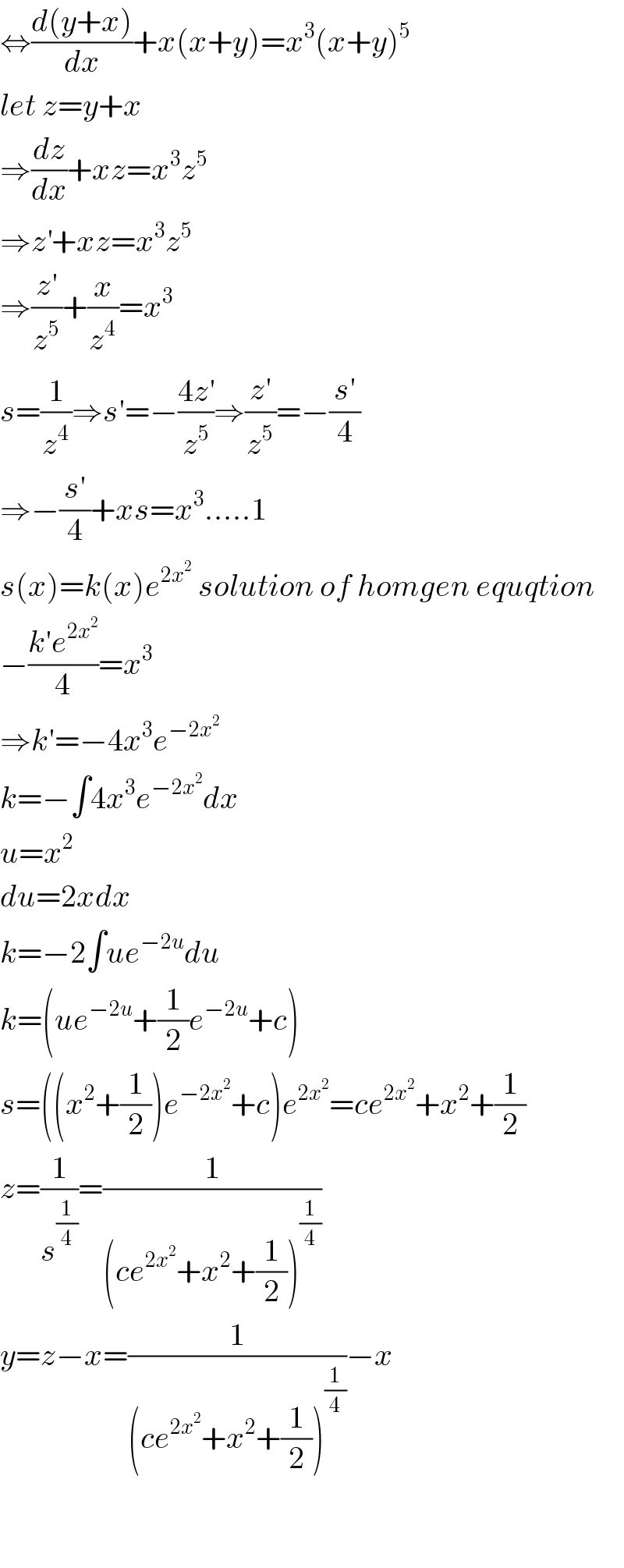
$$\Leftrightarrow\frac{{d}\left({y}+{x}\right)}{{dx}}+{x}\left({x}+{y}\right)={x}^{\mathrm{3}} \left({x}+{y}\right)^{\mathrm{5}} \\ $$$${let}\:{z}={y}+{x} \\ $$$$\Rightarrow\frac{{dz}}{{dx}}+{xz}={x}^{\mathrm{3}} {z}^{\mathrm{5}} \\ $$$$\Rightarrow{z}^{'} +{xz}={x}^{\mathrm{3}} {z}^{\mathrm{5}} \\ $$$$\Rightarrow\frac{{z}'}{{z}^{\mathrm{5}} }+\frac{{x}}{{z}^{\mathrm{4}} }={x}^{\mathrm{3}} \\ $$$${s}=\frac{\mathrm{1}}{{z}^{\mathrm{4}} }\Rightarrow{s}'=−\frac{\mathrm{4}{z}^{'} }{{z}^{\mathrm{5}} }\Rightarrow\frac{{z}'}{{z}^{\mathrm{5}} }=−\frac{{s}'}{\mathrm{4}} \\ $$$$\Rightarrow−\frac{{s}'}{\mathrm{4}}+{xs}={x}^{\mathrm{3}} …..\mathrm{1} \\ $$$${s}\left({x}\right)={k}\left({x}\right){e}^{\mathrm{2}{x}^{\mathrm{2}} } \:{solution}\:{of}\:{homgen}\:{equqtion} \\ $$$$−\frac{{k}'{e}^{\mathrm{2}{x}^{\mathrm{2}} } }{\mathrm{4}}={x}^{\mathrm{3}} \\ $$$$\Rightarrow{k}'=−\mathrm{4}{x}^{\mathrm{3}} {e}^{−\mathrm{2}{x}^{\mathrm{2}} } \\ $$$${k}=−\int\mathrm{4}{x}^{\mathrm{3}} {e}^{−\mathrm{2}{x}^{\mathrm{2}} } {dx} \\ $$$${u}={x}^{\mathrm{2}} \\ $$$${du}=\mathrm{2}{xdx} \\ $$$${k}=−\mathrm{2}\int{ue}^{−\mathrm{2}{u}} {du} \\ $$$${k}=\left({ue}^{−\mathrm{2}{u}} +\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{u}} +{c}\right) \\ $$$${s}=\left(\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right){e}^{−\mathrm{2}{x}^{\mathrm{2}} } +{c}\right){e}^{\mathrm{2}{x}^{\mathrm{2}} } ={ce}^{\mathrm{2}{x}^{\mathrm{2}} } +{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${z}=\frac{\mathrm{1}}{{s}^{\frac{\mathrm{1}}{\mathrm{4}}} }=\frac{\mathrm{1}}{\left({ce}^{\mathrm{2}{x}^{\mathrm{2}} } +{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} } \\ $$$${y}={z}−{x}=\frac{\mathrm{1}}{\left({ce}^{\mathrm{2}{x}^{\mathrm{2}} } +{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }−{x} \\ $$$$ \\ $$$$ \\ $$
