Menu Close

Question-67772

Tinku Tara 0 Comments
Pin




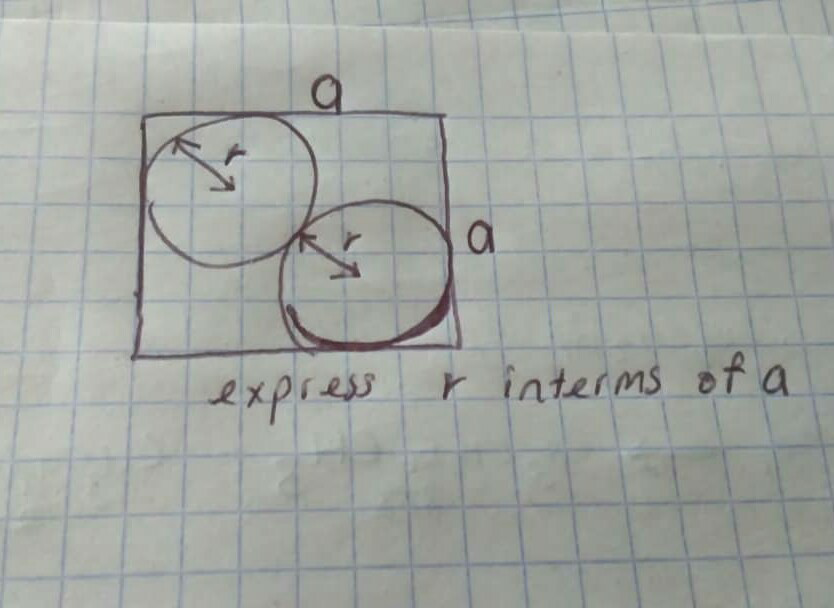
Question Number 67772 by TawaTawa last updated on 31/Aug/19
Commented by Prithwish sen last updated on 31/Aug/19
r=a((((√2)−1)/( (√2))))
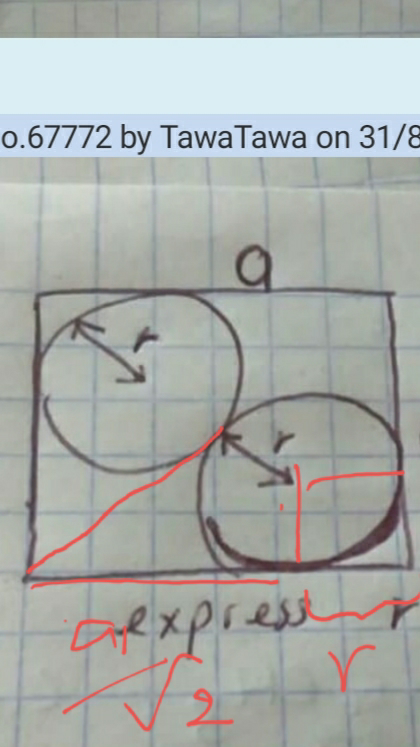
$$\boldsymbol{\mathrm{r}}=\boldsymbol{\mathrm{a}}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$
Commented by Prithwish sen last updated on 31/Aug/19
Commented by TawaTawa last updated on 31/Aug/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 31/Aug/19
the circles intersect each others in the same point where the diagonals of the square intersect ⇒ each circle is the incircle of a triangle with sides a, a, a(√2) Heron′s formula again, for a triangle with sides a, b, c: r_I =(δ/(2(a+b+c))) δ=(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) in our case δ=2a^2 r_I =(1−((√2)/2))a
$$\mathrm{the}\:\mathrm{circles}\:\mathrm{intersect}\:\mathrm{each}\:\mathrm{others}\:\mathrm{in}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{point}\:\mathrm{where}\:\mathrm{the}\:\mathrm{diagonals}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:\mathrm{intersect} \\ $$$$\Rightarrow\:\mathrm{each}\:\mathrm{circle}\:\mathrm{is}\:\mathrm{the}\:\mathrm{incircle}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{with} \\ $$$$\mathrm{sides}\:{a},\:{a},\:{a}\sqrt{\mathrm{2}} \\ $$$$\mathrm{Heron}'\mathrm{s}\:\mathrm{formula}\:\mathrm{again},\:\mathrm{for}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{with} \\ $$$$\mathrm{sides}\:{a},\:{b},\:{c}: \\ $$$${r}_{{I}} =\frac{\delta}{\mathrm{2}\left({a}+{b}+{c}\right)} \\ $$$$\delta=\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)} \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case} \\ $$$$\delta=\mathrm{2}{a}^{\mathrm{2}} \\ $$$${r}_{{I}} =\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right){a} \\ $$
Commented by Prithwish sen last updated on 31/Aug/19
Thank you sir.
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 31/Aug/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 31/Aug/19
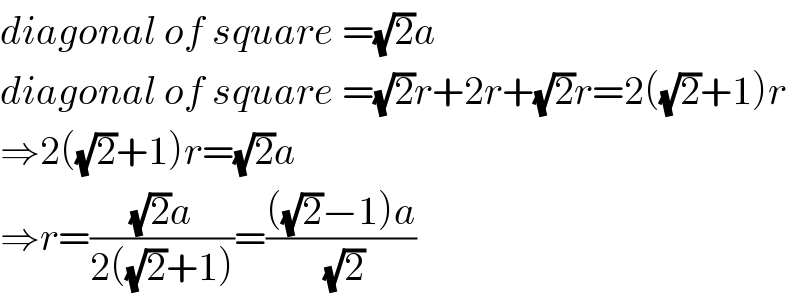
diagonal of square =(√2)a diagonal of square =(√2)r+2r+(√2)r=2((√2)+1)r ⇒2((√2)+1)r=(√2)a ⇒r=(((√2)a)/(2((√2)+1)))=((((√2)−1)a)/( (√2)))
$${diagonal}\:{of}\:{square}\:=\sqrt{\mathrm{2}}{a} \\ $$$${diagonal}\:{of}\:{square}\:=\sqrt{\mathrm{2}}{r}+\mathrm{2}{r}+\sqrt{\mathrm{2}}{r}=\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){r} \\ $$$$\Rightarrow\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){r}=\sqrt{\mathrm{2}}{a} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{2}}{a}}{\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}=\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right){a}}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by TawaTawa last updated on 31/Aug/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Prithwish sen last updated on 31/Aug/19
thank sir
$$\mathrm{thank}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *