Question Number 67807 by TawaTawa last updated on 31/Aug/19

Commented by MJS last updated on 01/Sep/19
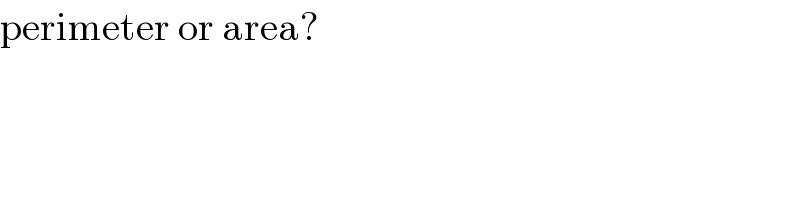
$$\mathrm{perimeter}\:\mathrm{or}\:\mathrm{area}? \\ $$
Commented by TawaTawa last updated on 01/Sep/19
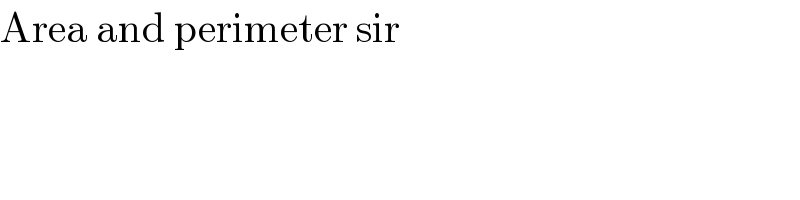
$$\mathrm{Area}\:\mathrm{and}\:\mathrm{perimeter}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 02/Sep/19
![parabola p: y=x^2 line AD l_1 : y=−(√3)x+2(√3) line BC l_2 : y=−(√3)x+4(√3) D=p∩l_1 = ((((−(√3)+(√(3+8(√3))))/2)),(((3+4(√3)−(√(9+24(√3))))/2)) ) C=p∩l_2 = ((((−(√3)+(√(3+16(√3))))/2)),(((3+8(√3)−(√(9+48(√3))))/2)) ) the length of the parabola ∫_a ^b (√(1+(f′(x))^2 ))dx ∫_a ^b (√(1+4x^2 ))dx=[(1/2)x(√(1+4x^2 ))+(1/4)ln (2x+(√(1+4x^2 )))]_a ^b ≈2.33536 ∣AB∣=2 ∣AD∣≈1.62640 ∣BC∣≈4.19014 perimeter ≈10.1519 area=∫_a ^b pdx+∫_b ^4 l_2 dx−∫_a ^2 l_1 dx≈4.97554 this example doesn′t resolve to “nice” solutiond](https://www.tinkutara.com/question/Q67979.png)
$$\mathrm{parabola}\:{p}:\:{y}={x}^{\mathrm{2}} \\ $$$$\mathrm{line}\:{AD}\:{l}_{\mathrm{1}} :\:{y}=−\sqrt{\mathrm{3}}{x}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{line}\:{BC}\:{l}_{\mathrm{2}} :\:{y}=−\sqrt{\mathrm{3}}{x}+\mathrm{4}\sqrt{\mathrm{3}} \\ $$$${D}={p}\cap{l}_{\mathrm{1}} =\begin{pmatrix}{\frac{−\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}+\mathrm{8}\sqrt{\mathrm{3}}}}{\mathrm{2}}}\\{\frac{\mathrm{3}+\mathrm{4}\sqrt{\mathrm{3}}−\sqrt{\mathrm{9}+\mathrm{24}\sqrt{\mathrm{3}}}}{\mathrm{2}}}\end{pmatrix} \\ $$$${C}={p}\cap{l}_{\mathrm{2}} =\begin{pmatrix}{\frac{−\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}+\mathrm{16}\sqrt{\mathrm{3}}}}{\mathrm{2}}}\\{\frac{\mathrm{3}+\mathrm{8}\sqrt{\mathrm{3}}−\sqrt{\mathrm{9}+\mathrm{48}\sqrt{\mathrm{3}}}}{\mathrm{2}}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{parabola} \\ $$$$\underset{{a}} {\overset{{b}} {\int}}\sqrt{\mathrm{1}+\left({f}'\left({x}\right)\right)^{\mathrm{2}} }{dx} \\ $$$$\underset{{a}} {\overset{{b}} {\int}}\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}=\left[\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\right)\right]_{{a}} ^{{b}} \\ $$$$\approx\mathrm{2}.\mathrm{33536} \\ $$$$\mid{AB}\mid=\mathrm{2} \\ $$$$\mid{AD}\mid\approx\mathrm{1}.\mathrm{62640} \\ $$$$\mid{BC}\mid\approx\mathrm{4}.\mathrm{19014} \\ $$$$\mathrm{perimeter}\:\approx\mathrm{10}.\mathrm{1519} \\ $$$$ \\ $$$$\mathrm{area}=\underset{{a}} {\overset{{b}} {\int}}{pdx}+\underset{{b}} {\overset{\mathrm{4}} {\int}}{l}_{\mathrm{2}} {dx}−\underset{{a}} {\overset{\mathrm{2}} {\int}}{l}_{\mathrm{1}} {dx}\approx\mathrm{4}.\mathrm{97554} \\ $$$$ \\ $$$$\mathrm{this}\:\mathrm{example}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{resolve}\:\mathrm{to}\:“\mathrm{nice}''\:\mathrm{solutiond} \\ $$
Commented by TawaTawa last updated on 03/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$
