Question-67813

Question Number 67813 by mr W last updated on 31/Aug/19

Commented by mr W last updated on 31/Aug/19

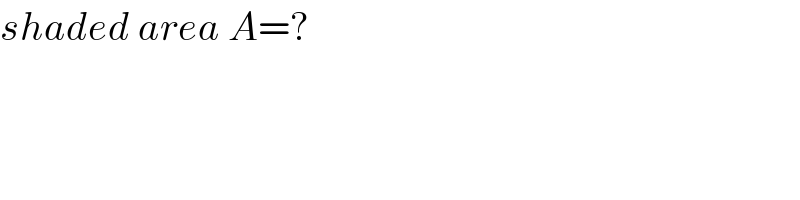
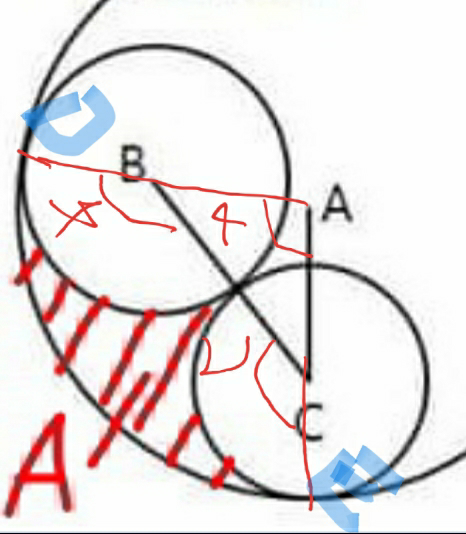
$${shaded}\:{area}\:{A}=? \\ $$

Commented by Prithwish sen last updated on 31/Aug/19

R_A =13,R_B =6,R_C =5 AB=7,BC=6+5=11,AC=11−5=6 s=((7+11+6)/2) = 12 Sin(α/2)=(√((((s−AC)(s−AB))/(AC×AB)) )) = (√(5/7)) 𝛂 ∽ 115° Sin((ABC)/2) =(√((((12−7)(12−11))/(7×11)) ))⇒𝛃∽150° Sin ((ACB)/2) =(√(((12−6)(12−11))/(6×11))) ⇒𝛄∽115° Area of △ABC = (1/2)AB×AC×sinα ∽ 19.03..(i) Area of the sector of the circle C , S_c = 𝛑(R_c )^2 ×((115)/(360)) ∽ 25.08...(ii) Smilarly S_B = 𝛑(R_B )^2 ×((150)/(360)) ∽ 47.12 ....(iii) And S_A = 𝛑(R_A )^2 ×((115)/(360)) ∽ 169.6.....(iv) ∴ Area of the shadded portion = (iv)−[(i)+(ii)+(iii)] ∽ 78.37 Sir waiting for your feedback.

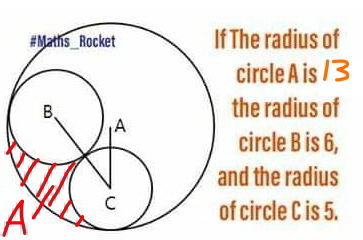
$$\mathrm{R}_{\mathrm{A}} =\mathrm{13},\mathrm{R}_{\mathrm{B}} =\mathrm{6},\mathrm{R}_{\mathrm{C}} =\mathrm{5} \\ $$$$\mathrm{AB}=\mathrm{7},\mathrm{BC}=\mathrm{6}+\mathrm{5}=\mathrm{11},\mathrm{AC}=\mathrm{11}−\mathrm{5}=\mathrm{6} \\ $$$$\mathrm{s}=\frac{\mathrm{7}+\mathrm{11}+\mathrm{6}}{\mathrm{2}}\:=\:\mathrm{12} \\ $$$$\mathrm{Sin}\frac{\alpha}{\mathrm{2}}=\sqrt{\frac{\left(\mathrm{s}−\mathrm{AC}\right)\left(\mathrm{s}−\mathrm{AB}\right)}{\mathrm{AC}×\mathrm{AB}}\:}\:=\:\sqrt{\frac{\mathrm{5}}{\mathrm{7}}}\: \\ $$$$\boldsymbol{\alpha}\:\backsim\:\:\mathrm{115}°\: \\ $$$$\mathrm{Sin}\frac{\mathrm{ABC}}{\mathrm{2}}\:=\sqrt{\frac{\left(\mathrm{12}−\mathrm{7}\right)\left(\mathrm{12}−\mathrm{11}\right)}{\mathrm{7}×\mathrm{11}}\:}\Rightarrow\boldsymbol{\beta}\backsim\mathrm{150}° \\ $$$$\mathrm{Sin}\:\frac{\mathrm{ACB}}{\mathrm{2}}\:=\sqrt{\frac{\left(\mathrm{12}−\mathrm{6}\right)\left(\mathrm{12}−\mathrm{11}\right)}{\mathrm{6}×\mathrm{11}}}\:\Rightarrow\boldsymbol{\gamma}\backsim\mathrm{115}° \\ $$$$\boldsymbol{\mathrm{Area}}\:\boldsymbol{\mathrm{of}}\:\bigtriangleup\boldsymbol{\mathrm{ABC}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{AB}×\mathrm{AC}×\mathrm{sin}\alpha\:\backsim\:\mathrm{19}.\mathrm{03}..\left(\mathrm{i}\right) \\ $$$$\boldsymbol{\mathrm{Area}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{sector}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{circle}}\:\boldsymbol{\mathrm{C}}\:, \\ $$$$\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{c}}} \:=\:\boldsymbol{\pi}\left(\boldsymbol{\mathrm{R}}_{\boldsymbol{\mathrm{c}}} \right)^{\mathrm{2}} ×\frac{\mathrm{115}}{\mathrm{360}}\:\backsim\:\mathrm{25}.\mathrm{08}…\left(\mathrm{ii}\right) \\ $$$$\boldsymbol{\mathrm{Smilarly}}\:\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{B}}} =\:\boldsymbol{\pi}\left(\boldsymbol{\mathrm{R}}_{\boldsymbol{\mathrm{B}}} \right)^{\mathrm{2}} ×\frac{\mathrm{150}}{\mathrm{360}}\:\backsim\:\mathrm{47}.\mathrm{12}\:….\left(\mathrm{iii}\right) \\ $$$$\boldsymbol{\mathrm{And}}\:\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{A}}} =\:\boldsymbol{\pi}\left(\boldsymbol{\mathrm{R}}_{\boldsymbol{\mathrm{A}}} \right)^{\mathrm{2}} ×\frac{\mathrm{115}}{\mathrm{360}}\:\:\backsim\:\mathrm{169}.\mathrm{6}…..\left(\mathrm{iv}\right) \\ $$$$\therefore\:\boldsymbol{\mathrm{Area}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{shadded}}\:\boldsymbol{\mathrm{portion}} \\ $$$$=\:\left(\boldsymbol{\mathrm{iv}}\right)−\left[\left(\boldsymbol{\mathrm{i}}\right)+\left(\boldsymbol{\mathrm{ii}}\right)+\left(\boldsymbol{\mathrm{iii}}\right)\right]\:\backsim\:\mathrm{78}.\mathrm{37} \\ $$$$\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{waiting}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{feedback}}. \\ $$

Commented by mr W last updated on 01/Sep/19

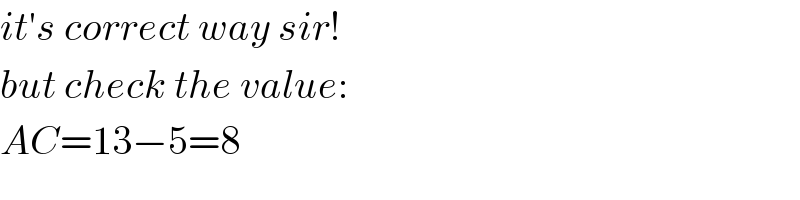
it′s correct way sir! but check the value: AC=13−5=8

$${it}'{s}\:{correct}\:{way}\:{sir}! \\ $$$${but}\:{check}\:{the}\:{value}: \\ $$$${AC}=\mathrm{13}−\mathrm{5}=\mathrm{8} \\ $$

Commented by Prithwish sen last updated on 01/Sep/19

$$\mathrm{oh}!\:\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}.\: \\ $$

Commented by Rasheed.Sindhi last updated on 01/Sep/19

Sir prithwish sen please see my answer to Q#67697.There I have tried to apply Chinese Remainder Theorm in case of polynomials.Your critical remarks are important for me!

Commented by Prithwish sen last updated on 01/Sep/19

Sir first of all please forgive me for giving delayed response. There is something going wrong as I am not getting any notification. So it is my request to the developer please fix it. Now back to the problem sir you have done a wonderful job. I dont find anything wrong in your solution. Thanks again sir.

$$\mathrm{Sir}\:\mathrm{first}\:\mathrm{of}\:\mathrm{all}\:\mathrm{please}\:\mathrm{forgive}\:\mathrm{me}\:\mathrm{for}\:\mathrm{giving} \\ $$$$\mathrm{delayed}\:\mathrm{response}.\:\mathrm{There}\:\mathrm{is}\:\mathrm{something}\:\mathrm{going} \\ $$$$\mathrm{wrong}\:\mathrm{as}\:\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{any}\:\mathrm{notification}. \\ $$$$\mathrm{So}\:\mathrm{it}\:\mathrm{is}\:\mathrm{my}\:\mathrm{request}\:\mathrm{to}\:\mathrm{the}\:\mathrm{developer}\:\mathrm{please} \\ $$$$\mathrm{fix}\:\mathrm{it}.\:\mathrm{Now}\:\mathrm{back}\:\mathrm{to}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{sir}\:\mathrm{you}\:\mathrm{have} \\ $$$$\mathrm{done}\:\mathrm{a}\:\mathrm{wonderful}\:\mathrm{job}.\:\mathrm{I}\:\mathrm{dont}\:\mathrm{find}\:\mathrm{anything} \\ $$$$\mathrm{wrong}\:\mathrm{in}\:\mathrm{your}\:\mathrm{solution}.\:\mathrm{Thanks}\:\mathrm{again}\:\mathrm{sir}. \\ $$

Commented by Rasheed.Sindhi last updated on 02/Sep/19

TThhaannkkss a lot sir! Actually I haven′t seen use of the theorm in polynomials. ∴ I was not confident! thanx again sir!

$$\mathrm{TThhaannkkss}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir}! \\ $$$$\mathrm{Actually}\:\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{seen}\:\mathrm{use}\:\mathrm{of}\:\mathrm{the}\:\mathrm{theorm}\:\mathrm{in} \\ $$$$\mathrm{polynomials}.\:\:\therefore\:\mathrm{I}\:\mathrm{was}\:\mathrm{not}\:\mathrm{confident}!\: \\ $$$$\mathrm{thanx}\:\mathrm{again}\:\mathrm{sir}! \\ $$

Commented by Prithwish sen last updated on 02/Sep/19