Question Number 67826 by peter frank last updated on 31/Aug/19

Commented by gunawan last updated on 01/Sep/19
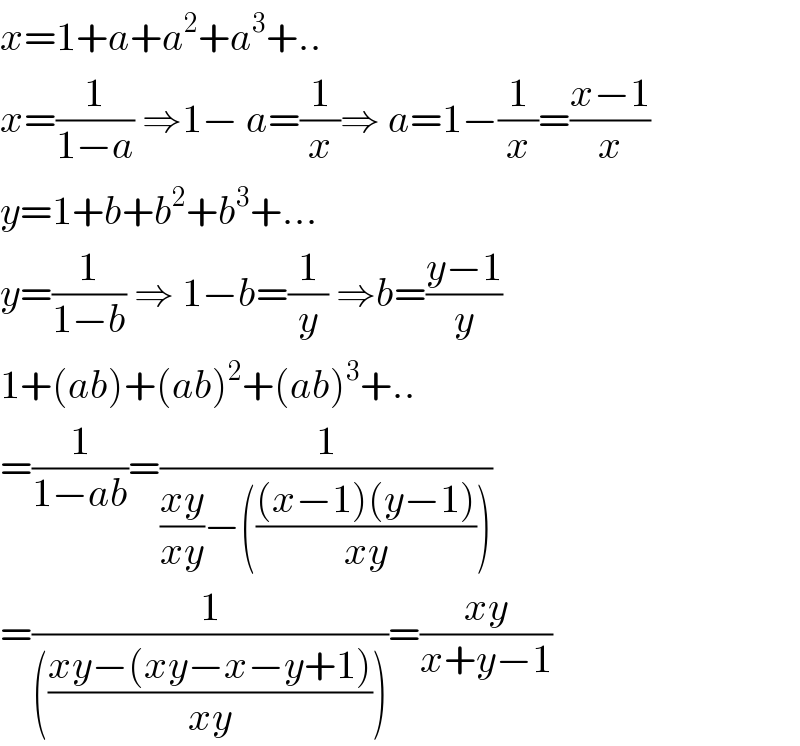
$${x}=\mathrm{1}+{a}+{a}^{\mathrm{2}} +{a}^{\mathrm{3}} +.. \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{1}−{a}}\:\Rightarrow\mathrm{1}−\:{a}=\frac{\mathrm{1}}{{x}}\Rightarrow\:{a}=\mathrm{1}−\frac{\mathrm{1}}{{x}}=\frac{{x}−\mathrm{1}}{{x}} \\ $$$${y}=\mathrm{1}+{b}+{b}^{\mathrm{2}} +{b}^{\mathrm{3}} +… \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{1}−{b}}\:\Rightarrow\:\mathrm{1}−{b}=\frac{\mathrm{1}}{{y}}\:\Rightarrow{b}=\frac{{y}−\mathrm{1}}{{y}}\: \\ $$$$\mathrm{1}+\left({ab}\right)+\left({ab}\right)^{\mathrm{2}} +\left({ab}\right)^{\mathrm{3}} +.. \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{ab}}=\frac{\mathrm{1}}{\frac{{xy}}{{xy}}−\left(\frac{\left({x}−\mathrm{1}\right)\left({y}−\mathrm{1}\right)}{{xy}}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\frac{{xy}−\left({xy}−{x}−{y}+\mathrm{1}\right)}{{xy}}\right)}=\frac{{xy}}{{x}+{y}−\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 01/Sep/19

$${its}\:{not}\:{correct}\:{if}\:\mid{a}\mid\geqslant\mathrm{1}\:{or}\:\:\mid{b}\mid\geqslant\mathrm{1}…! \\ $$
Commented by peter frank last updated on 01/Sep/19

$${thank}\:{you}\: \\ $$
Commented by peter frank last updated on 01/Sep/19

$${thank}\:{you}\: \\ $$
Answered by mind is power last updated on 01/Sep/19
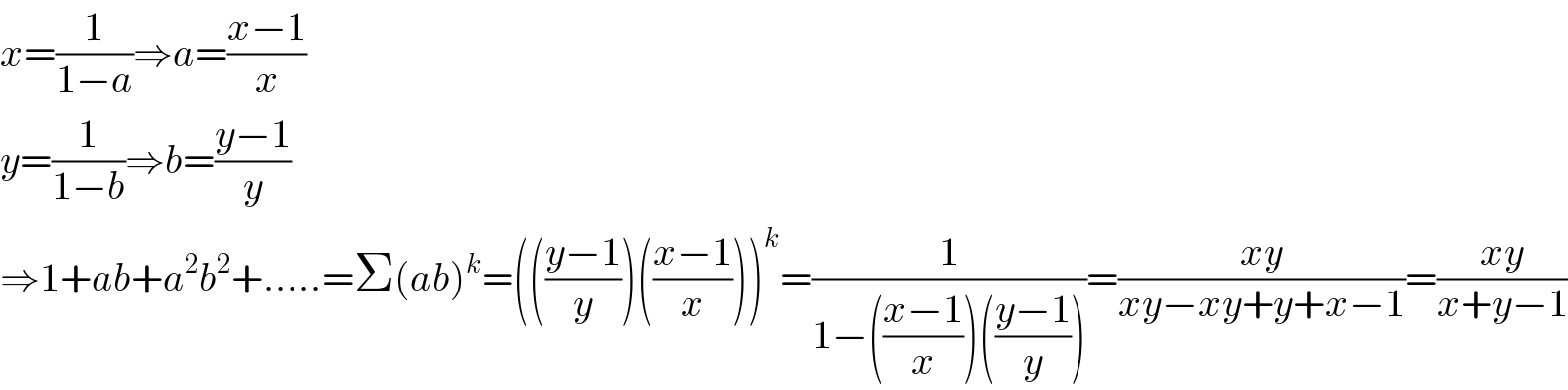
$${x}=\frac{\mathrm{1}}{\mathrm{1}−{a}}\Rightarrow{a}=\frac{{x}−\mathrm{1}}{{x}} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{1}−{b}}\Rightarrow{b}=\frac{{y}−\mathrm{1}}{{y}} \\ $$$$\Rightarrow\mathrm{1}+{ab}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} +…..=\Sigma\left({ab}\right)^{{k}} =\left(\left(\frac{{y}−\mathrm{1}}{{y}}\right)\left(\frac{{x}−\mathrm{1}}{{x}}\right)\right)^{{k}} =\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{{x}−\mathrm{1}}{{x}}\right)\left(\frac{{y}−\mathrm{1}}{{y}}\right)}=\frac{{xy}}{{xy}−{xy}+{y}+{x}−\mathrm{1}}=\frac{{xy}}{{x}+{y}−\mathrm{1}} \\ $$
Answered by rrebo5637@gmail.com last updated on 01/Sep/19

