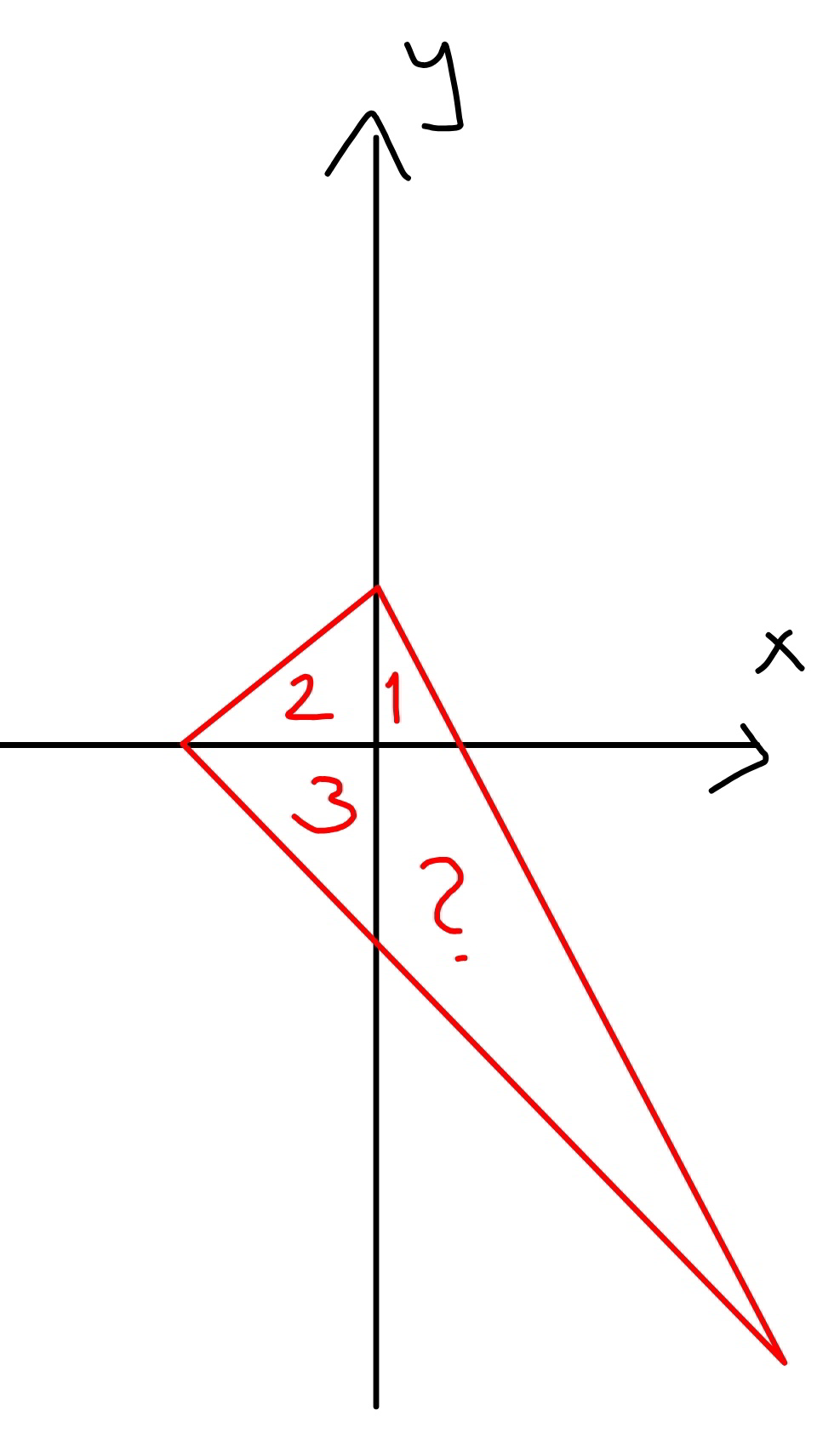
Question Number 67852 by mr W last updated on 01/Sep/19
Commented by Prithwish sen last updated on 01/Sep/19

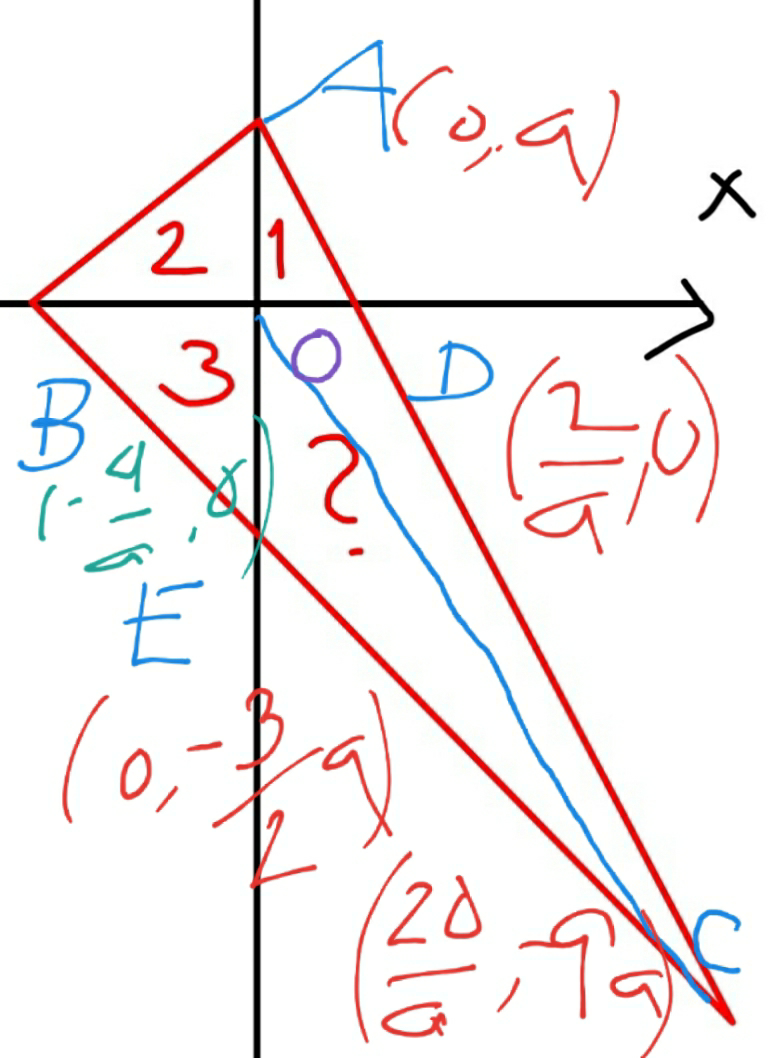
$$ \\ $$$$\boldsymbol{\mathrm{A}}=\left(\mathrm{0},\boldsymbol{\mathrm{a}}\right),\:\boldsymbol{\mathrm{B}}\:=\:\left(\frac{−\mathrm{4}}{\boldsymbol{\mathrm{a}}},\mathrm{0}\right),\boldsymbol{\mathrm{C}}=\left(\frac{\mathrm{20}}{\boldsymbol{\mathrm{a}}},−\mathrm{9}\boldsymbol{\mathrm{a}}\right),\boldsymbol{\mathrm{D}}=\left(\frac{\mathrm{2}}{\boldsymbol{\mathrm{a}}},\mathrm{0}\right) \\ $$$$\boldsymbol{\mathrm{E}}=\left(\mathrm{0},\frac{−\mathrm{3}\boldsymbol{\mathrm{a}}}{\mathrm{2}}\right)\: \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{line}\:\mathrm{passing}\:\mathrm{through}\:\mathrm{A}\:\mathrm{and}\:\mathrm{D} \\ $$$$\boldsymbol{\mathrm{AC}}\Rightarrow\mathrm{a}^{\mathrm{2}} \mathrm{x}+\mathrm{2y}−\mathrm{2a}=\mathrm{0}….\left(\mathrm{i}\right) \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{line}\:\mathrm{passing}\:\mathrm{through}\:\mathrm{B}\:\mathrm{and}\:\mathrm{E} \\ $$$$\boldsymbol{\mathrm{BC}}\Rightarrow\mathrm{3a}^{\mathrm{2}} \mathrm{x}+\mathrm{8y}+\mathrm{12a}=….\left(\mathrm{ii}\right) \\ $$$$\mathrm{Solving}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right)\:\mathrm{we}\:\mathrm{get}\:\boldsymbol{\mathrm{C}} \\ $$$$\therefore\:\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{required}}\:\boldsymbol{\mathrm{area}}\:=\:\bigtriangleup\mathrm{ODC}+\bigtriangleup\mathrm{OEC} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{a}}×\mathrm{9a}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3a}}{\mathrm{2}}×\frac{\mathrm{20}}{\mathrm{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{9}+\mathrm{15}\:=\:\mathrm{24} \\ $$
Commented by Prithwish sen last updated on 01/Sep/19
Commented by mr W last updated on 01/Sep/19
$${correct}!\:{thanks}\:{sir}! \\ $$
Commented by Prithwish sen last updated on 02/Sep/19

$$\mathrm{welcome}\:\mathrm{sir}. \\ $$
Answered by MJS last updated on 01/Sep/19
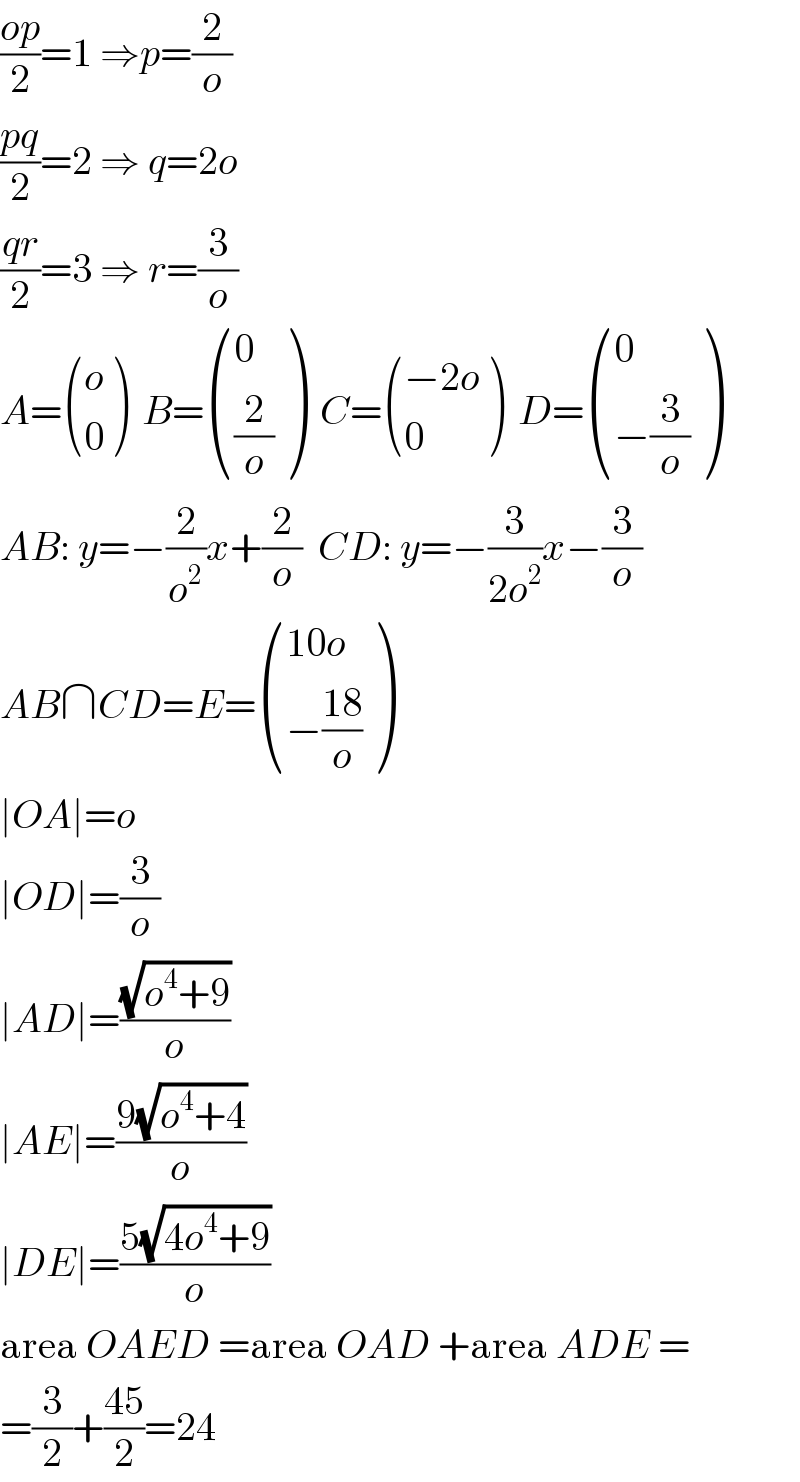
$$\frac{{op}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow{p}=\frac{\mathrm{2}}{{o}} \\ $$$$\frac{{pq}}{\mathrm{2}}=\mathrm{2}\:\Rightarrow\:{q}=\mathrm{2}{o} \\ $$$$\frac{{qr}}{\mathrm{2}}=\mathrm{3}\:\Rightarrow\:{r}=\frac{\mathrm{3}}{{o}} \\ $$$${A}=\begin{pmatrix}{{o}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{\frac{\mathrm{2}}{{o}}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{−\mathrm{2}{o}}\\{\mathrm{0}}\end{pmatrix}\:\:{D}=\begin{pmatrix}{\mathrm{0}}\\{−\frac{\mathrm{3}}{{o}}}\end{pmatrix} \\ $$$${AB}:\:{y}=−\frac{\mathrm{2}}{{o}^{\mathrm{2}} }{x}+\frac{\mathrm{2}}{{o}}\:\:{CD}:\:{y}=−\frac{\mathrm{3}}{\mathrm{2}{o}^{\mathrm{2}} }{x}−\frac{\mathrm{3}}{{o}} \\ $$$${AB}\cap{CD}={E}=\begin{pmatrix}{\mathrm{10}{o}}\\{−\frac{\mathrm{18}}{{o}}}\end{pmatrix} \\ $$$$\mid{OA}\mid={o} \\ $$$$\mid{OD}\mid=\frac{\mathrm{3}}{{o}} \\ $$$$\mid{AD}\mid=\frac{\sqrt{{o}^{\mathrm{4}} +\mathrm{9}}}{{o}} \\ $$$$\mid{AE}\mid=\frac{\mathrm{9}\sqrt{{o}^{\mathrm{4}} +\mathrm{4}}}{{o}} \\ $$$$\mid{DE}\mid=\frac{\mathrm{5}\sqrt{\mathrm{4}{o}^{\mathrm{4}} +\mathrm{9}}}{{o}} \\ $$$$\mathrm{area}\:{OAED}\:=\mathrm{area}\:{OAD}\:+\mathrm{area}\:{ADE}\:= \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{45}}{\mathrm{2}}=\mathrm{24} \\ $$
Commented by mr W last updated on 01/Sep/19

$${thanks}\:{sir}! \\ $$
