Question Number 67860 by TawaTawa last updated on 01/Sep/19

Commented by TawaTawa last updated on 01/Sep/19

$$\mathrm{Find}\:\mathrm{angle}\:\:\mathrm{a} \\ $$
Commented by mr W last updated on 01/Sep/19

$${a}=\mathrm{72}° \\ $$
Commented by TawaTawa last updated on 01/Sep/19

$$\mathrm{Correct},\:\mathrm{please}\:\mathrm{workings}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 01/Sep/19

$${let}\:{BC}=\mathrm{1} \\ $$$$\angle{B}=\mathrm{12}+\mathrm{36}=\mathrm{48}=\mathrm{30}+\mathrm{18}=\angle{C} \\ $$$$\Rightarrow{AB}={AC}=\frac{{BC}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{cos}\:\angle{B}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{48}°} \\ $$$$\frac{{BD}}{\mathrm{sin}\:\mathrm{30}°}=\frac{{BC}}{\mathrm{sin}\:\left(\mathrm{12}+\mathrm{30}\right)}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{42}°}=\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{48}°} \\ $$$$\Rightarrow{BD}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{48}°}={BA} \\ $$$$\mathrm{2}{a}+\mathrm{36}=\mathrm{180} \\ $$$$\Rightarrow{a}=\frac{\mathrm{180}−\mathrm{36}}{\mathrm{2}}=\mathrm{72}° \\ $$
Commented by TawaTawa last updated on 01/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 02/Sep/19

$$\mathrm{Sir},\:\mathrm{why}\:\mathrm{did}\:\mathrm{you}\:\mathrm{let}\:\:\mathrm{BC}\:=\:\mathrm{1},\:\:\mathrm{and}\:\mathrm{when}\:\mathrm{can}\:\mathrm{i}\:\mathrm{use}\:\mathrm{it}\:\mathrm{in}\:\mathrm{question}. \\ $$
Commented by mr W last updated on 03/Sep/19
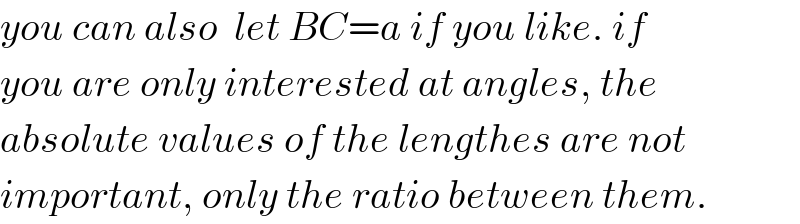
$${you}\:{can}\:{also}\:\:{let}\:{BC}={a}\:{if}\:{you}\:{like}.\:{if} \\ $$$${you}\:{are}\:{only}\:{interested}\:{at}\:{angles},\:{the} \\ $$$${absolute}\:{values}\:{of}\:{the}\:{lengthes}\:{are}\:{not} \\ $$$${important},\:{only}\:{the}\:{ratio}\:{between}\:{them}. \\ $$
Commented by TawaTawa last updated on 06/Sep/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
