Menu Close

Question-67903

Tinku Tara 0 Comments
Pin




Question Number 67903 by rajesh4661kumar@gmail.com last updated on 02/Sep/19
Answered by $@ty@m123 last updated on 02/Sep/19
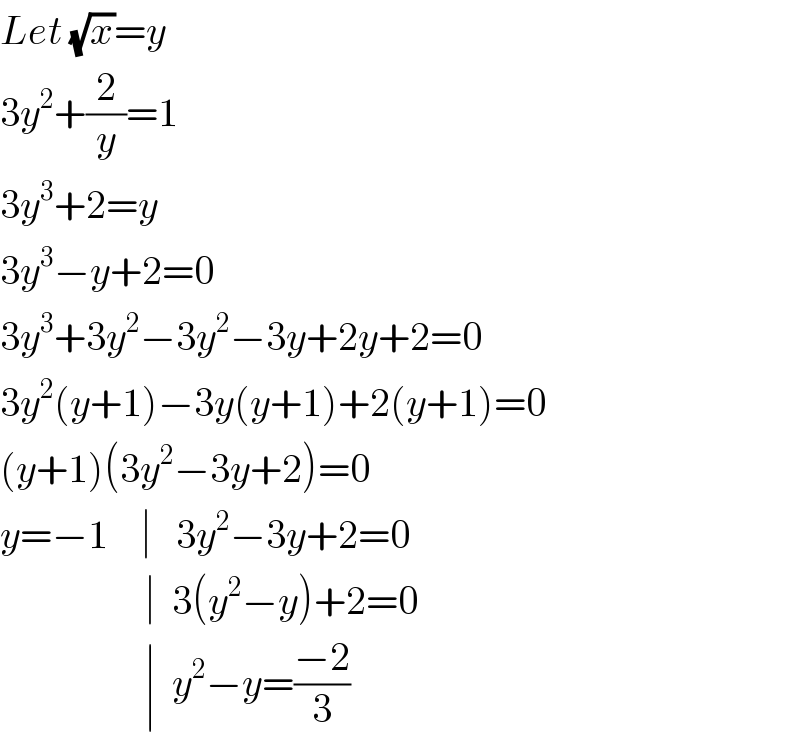
Let (√x)=y 3y^2 +(2/y)=1 3y^3 +2=y 3y^3 −y+2=0 3y^3 +3y^2 −3y^2 −3y+2y+2=0 3y^2 (y+1)−3y(y+1)+2(y+1)=0 (y+1)(3y^2 −3y+2)=0 y=−1 ∣ 3y^2 −3y+2=0 ∣ 3(y^2 −y)+2=0 ∣ y^2 −y=((−2)/3)
$${Let}\:\sqrt{{x}}={y} \\ $$$$\mathrm{3}{y}^{\mathrm{2}} +\frac{\mathrm{2}}{{y}}=\mathrm{1} \\ $$$$\mathrm{3}{y}^{\mathrm{3}} +\mathrm{2}={y} \\ $$$$\mathrm{3}{y}^{\mathrm{3}} −{y}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{3}{y}^{\mathrm{3}} +\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{2}{y}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{3}{y}^{\mathrm{2}} \left({y}+\mathrm{1}\right)−\mathrm{3}{y}\left({y}+\mathrm{1}\right)+\mathrm{2}\left({y}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({y}+\mathrm{1}\right)\left(\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{2}\right)=\mathrm{0} \\ $$$${y}=−\mathrm{1}\:\:\:\:\mid\:\:\:\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\:\mathrm{3}\left({y}^{\mathrm{2}} −{y}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\:{y}^{\mathrm{2}} −{y}=\frac{−\mathrm{2}}{\mathrm{3}} \\ $$
Commented by MJS last updated on 02/Sep/19
y=−1 ⇒ (√x)=−1 and this has no solution you get the right result but the path is wrong
$${y}=−\mathrm{1}\:\Rightarrow\:\sqrt{{x}}=−\mathrm{1}\:\mathrm{and}\:\mathrm{this}\:\mathrm{has}\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{right}\:\mathrm{result}\:\mathrm{but}\:\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Commented by Prithwish sen last updated on 02/Sep/19
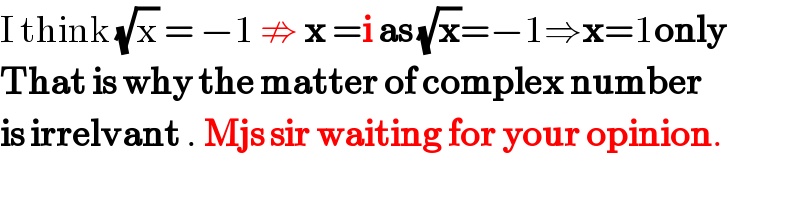
I think (√x) = −1 ⇏ x =i as (√x)=−1⇒x=1only That is why the matter of complex number is irrelvant . Mjs sir waiting for your opinion.
$$\mathrm{I}\:\mathrm{think}\:\sqrt{\mathrm{x}}\:=\:−\mathrm{1}\:\nRightarrow\:\boldsymbol{\mathrm{x}}\:=\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{as}}\:\sqrt{\boldsymbol{\mathrm{x}}}=−\mathrm{1}\Rightarrow\boldsymbol{\mathrm{x}}=\mathrm{1}\boldsymbol{\mathrm{only}} \\ $$$$\boldsymbol{\mathrm{That}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{why}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{matter}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{complex}}\:\boldsymbol{\mathrm{number}} \\ $$$$\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{irrelvant}}\:.\:\boldsymbol{\mathrm{Mjs}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{waiting}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{opinion}}. \\ $$
Commented by MJS last updated on 02/Sep/19
it′s not a matter of being broad or narrow minded. x^2 =−1 x^2 +1=0 (x−i)(x+i)=0 ⇒ x=±i (−i)^2 =−1 (+i)^2 =−1 x^3 =−1 x^3 +1=0 (x+1)(x^2 −x+1)=0 ⇒ x=−1∨x=(1/2)±((√3)/2)i (−1)^3 =−1 ((1/2)−((√3)/2)i)^3 =−1 ((1/2)+((√3)/2)i)^3 =−1 ... x^n =−1 the solutions form a cyclic n−gon x^(1/2) =−1 (1) what′s a cyclic (1/2)−gon? (2) x=re^(iθ) ; −1=e^(iπ) (√r)e^(i(θ/2)) =1e^(iπ) ⇒^(?) r=1∧θ=2π ⇔ x=e^(2πi) =1 but: (√1)=1 the problem is, if we square an equation we might get false solutions ⇒ we have to try these solutions in the original equation another problem: if (√1)=±1 we can forget the uniqueness of terms like (√((7/(16))−((√3)/4))) this would have 4 different values usually all n−roots are defined as the “natural” roots: (√4)=2 (√(−4))=2i (8)^(1/3) =2 ((−8))^(1/3) =−2 (this violates other laws, electronic calculators give ((−8))^(1/3) =1+(√3)i because the “natural” 3^(rd) root of 8e^(iπ) is (8)^(1/3) e^(i(π/3)) ) ... this also makes it complicated to calculate (−1)^(2/5) : (((−1)^2 ))^(1/5) ≠(((−1))^(1/5) )^2 in machine logic
$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{a}\:\mathrm{matter}\:\mathrm{of}\:\mathrm{being}\:\mathrm{broad}\:\mathrm{or}\:\mathrm{narrow} \\ $$$$\mathrm{minded}. \\ $$$${x}^{\mathrm{2}} =−\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\left({x}−\mathrm{i}\right)\left({x}+\mathrm{i}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\pm\mathrm{i} \\ $$$$\:\:\:\:\:\left(−\mathrm{i}\right)^{\mathrm{2}} =−\mathrm{1} \\ $$$$\:\:\:\:\:\left(+\mathrm{i}\right)^{\mathrm{2}} =−\mathrm{1} \\ $$$${x}^{\mathrm{3}} =−\mathrm{1} \\ $$$${x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}=−\mathrm{1}\vee{x}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\:\:\:\:\:\left(−\mathrm{1}\right)^{\mathrm{3}} =−\mathrm{1} \\ $$$$\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)^{\mathrm{3}} =−\mathrm{1} \\ $$$$\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)^{\mathrm{3}} =−\mathrm{1} \\ $$$$… \\ $$$$ \\ $$$${x}^{{n}} =−\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{solutions}\:\mathrm{form}\:\mathrm{a}\:\mathrm{cyclic}\:{n}−\mathrm{gon} \\ $$$$ \\ $$$${x}^{\frac{\mathrm{1}}{\mathrm{2}}} =−\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{what}'\mathrm{s}\:\mathrm{a}\:\mathrm{cyclic}\:\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{gon}? \\ $$$$\left(\mathrm{2}\right)\:{x}={r}\mathrm{e}^{\mathrm{i}\theta} ;\:−\mathrm{1}=\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\:\:\:\:\:\:\:\sqrt{{r}}\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} =\mathrm{1e}^{\mathrm{i}\pi} \\ $$$$\:\:\:\:\:\:\:\overset{?} {\Rightarrow}\:{r}=\mathrm{1}\wedge\theta=\mathrm{2}\pi\:\Leftrightarrow\:{x}=\mathrm{e}^{\mathrm{2}\pi\mathrm{i}} =\mathrm{1} \\ $$$$\mathrm{but}:\:\sqrt{\mathrm{1}}=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{problem}\:\mathrm{is},\:\mathrm{if}\:\mathrm{we}\:\mathrm{square}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{we} \\ $$$$\mathrm{might}\:\mathrm{get}\:\mathrm{false}\:\mathrm{solutions}\:\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{try} \\ $$$$\mathrm{these}\:\mathrm{solutions}\:\mathrm{in}\:\mathrm{the}\:\mathrm{original}\:\mathrm{equation} \\ $$$$ \\ $$$$\mathrm{another}\:\mathrm{problem}:\:\mathrm{if}\:\sqrt{\mathrm{1}}=\pm\mathrm{1}\:\mathrm{we}\:\mathrm{can}\:\mathrm{forget} \\ $$$$\mathrm{the}\:\mathrm{uniqueness}\:\mathrm{of}\:\mathrm{terms}\:\mathrm{like} \\ $$$$\sqrt{\frac{\mathrm{7}}{\mathrm{16}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}} \\ $$$$\mathrm{this}\:\mathrm{would}\:\mathrm{have}\:\mathrm{4}\:\mathrm{different}\:\mathrm{values} \\ $$$$ \\ $$$$\mathrm{usually}\:\mathrm{all}\:{n}−\mathrm{roots}\:\mathrm{are}\:\mathrm{defined}\:\mathrm{as}\:\mathrm{the}\:“\mathrm{natural}'' \\ $$$$\mathrm{roots}: \\ $$$$\sqrt{\mathrm{4}}=\mathrm{2} \\ $$$$\sqrt{−\mathrm{4}}=\mathrm{2i} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{8}}=\mathrm{2} \\ $$$$\sqrt[{\mathrm{3}}]{−\mathrm{8}}=−\mathrm{2}\:\left(\mathrm{this}\:\mathrm{violates}\:\mathrm{other}\:\mathrm{laws},\:\mathrm{electronic}\right. \\ $$$$\:\:\:\:\:\mathrm{calculators}\:\mathrm{give}\:\sqrt[{\mathrm{3}}]{−\mathrm{8}}=\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}\:\mathrm{because}\:\mathrm{the} \\ $$$$\left.\:\:\:\:\:“\mathrm{natural}''\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{root}\:\mathrm{of}\:\mathrm{8e}^{\mathrm{i}\pi} \:\mathrm{is}\:\sqrt[{\mathrm{3}}]{\mathrm{8}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} \right) \\ $$$$… \\ $$$$\mathrm{this}\:\mathrm{also}\:\mathrm{makes}\:\mathrm{it}\:\mathrm{complicated}\:\mathrm{to}\:\mathrm{calculate} \\ $$$$\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{5}}} :\:\sqrt[{\mathrm{5}}]{\left(−\mathrm{1}\right)^{\mathrm{2}} }\neq\left(\sqrt[{\mathrm{5}}]{−\mathrm{1}}\right)^{\mathrm{2}} \:\mathrm{in}\:\mathrm{machine}\:\mathrm{logic} \\ $$
Commented by Prithwish sen last updated on 02/Sep/19
Thanks sir. I appreciate for your effort.
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{for}\:\mathrm{your}\:\mathrm{effort}. \\ $$
Answered by MJS last updated on 02/Sep/19
3x+(2/( (√x)))=1 3x(√x)−(√x)+2=0 x=t^2 3t^2 ∣t∣−∣t∣+2=0 case 1: t<0 −3t^3 +t+2=0 −(t−1)(3t^2 +3t+2)=0 ⇒ t=1 but t<0 ⇒ no solution in R case 2: t>0 3t^3 −t+2=0 (t+1)(3t^2 −3t+2)=0 ⇒ t=−1 but t>0 ⇒ no solution in R but in both cases we get 2 complex solutions and with x=t^2 we have x=−(1/6)±((√(15))/6)i ⇒ x−(√x)=−(2/3)
$$\mathrm{3}{x}+\frac{\mathrm{2}}{\:\sqrt{{x}}}=\mathrm{1} \\ $$$$\mathrm{3}{x}\sqrt{{x}}−\sqrt{{x}}+\mathrm{2}=\mathrm{0} \\ $$$${x}={t}^{\mathrm{2}} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} \mid{t}\mid−\mid{t}\mid+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{case}\:\mathrm{1}:\:{t}<\mathrm{0} \\ $$$$−\mathrm{3}{t}^{\mathrm{3}} +{t}+\mathrm{2}=\mathrm{0} \\ $$$$−\left({t}−\mathrm{1}\right)\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}=\mathrm{1}\:\mathrm{but}\:{t}<\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{R} \\ $$$$\mathrm{case}\:\mathrm{2}:\:{t}>\mathrm{0} \\ $$$$\mathrm{3}{t}^{\mathrm{3}} −{t}+\mathrm{2}=\mathrm{0} \\ $$$$\left({t}+\mathrm{1}\right)\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}=−\mathrm{1}\:\mathrm{but}\:{t}>\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{R} \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{in}\:\mathrm{both}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{get}\:\mathrm{2}\:\mathrm{complex}\:\mathrm{solutions} \\ $$$$\mathrm{and}\:\mathrm{with}\:{x}={t}^{\mathrm{2}} \:\mathrm{we}\:\mathrm{have} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{6}}\pm\frac{\sqrt{\mathrm{15}}}{\mathrm{6}}\mathrm{i} \\ $$$$\Rightarrow\:{x}−\sqrt{{x}}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by MJS last updated on 02/Sep/19
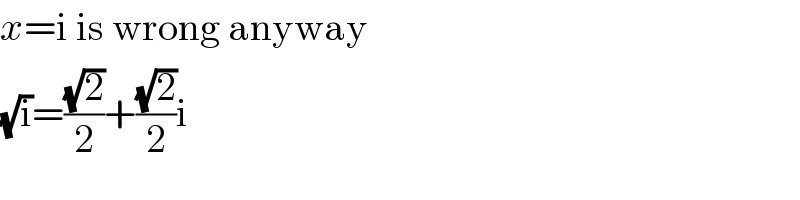
x=i is wrong anyway (√i)=((√2)/2)+((√2)/2)i
$${x}=\mathrm{i}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{anyway} \\ $$$$\sqrt{\mathrm{i}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *