Menu Close

Question-67907

Tinku Tara 0 Comments
Pin




Question Number 67907 by A8;15: last updated on 02/Sep/19
Commented by mathmax by abdo last updated on 02/Sep/19
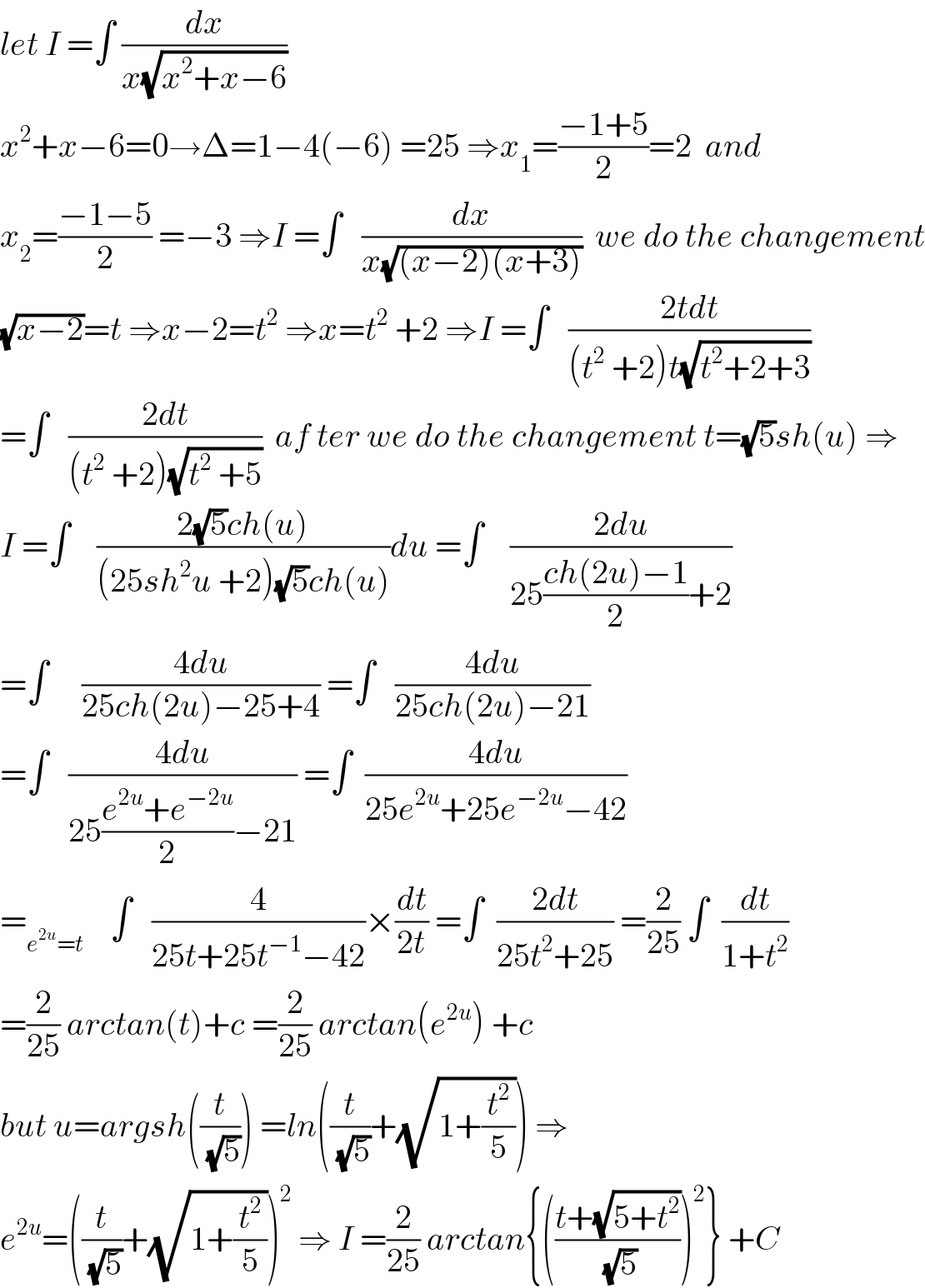
let I =∫ (dx/(x(√(x^2 +x−6)))) x^2 +x−6=0→Δ=1−4(−6) =25 ⇒x_1 =((−1+5)/2)=2 and x_2 =((−1−5)/2) =−3 ⇒I =∫ (dx/(x(√((x−2)(x+3))))) we do the changement (√(x−2))=t ⇒x−2=t^2 ⇒x=t^2 +2 ⇒I =∫ ((2tdt)/((t^2 +2)t(√(t^2 +2+3)))) =∫ ((2dt)/((t^2 +2)(√(t^2 +5)))) af ter we do the changement t=(√5)sh(u) ⇒ I =∫ ((2(√5)ch(u))/((25sh^2 u +2)(√5)ch(u)))du =∫ ((2du)/(25((ch(2u)−1)/2)+2)) =∫ ((4du)/(25ch(2u)−25+4)) =∫ ((4du)/(25ch(2u)−21)) =∫ ((4du)/(25((e^(2u) +e^(−2u) )/2)−21)) =∫ ((4du)/(25e^(2u) +25e^(−2u) −42)) =_(e^(2u) =t) ∫ (4/(25t+25t^(−1) −42))×(dt/(2t)) =∫ ((2dt)/(25t^2 +25)) =(2/(25)) ∫ (dt/(1+t^2 )) =(2/(25)) arctan(t)+c =(2/(25)) arctan(e^(2u) ) +c but u=argsh((t/( (√5)))) =ln((t/( (√5)))+(√(1+(t^2 /5)))) ⇒ e^(2u) =((t/( (√5)))+(√(1+(t^2 /5))))^2 ⇒ I =(2/(25)) arctan{(((t+(√(5+t^2 )))/( (√5))))^2 } +C
$${let}\:{I}\:=\int\:\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}−\mathrm{6}}} \\ $$$${x}^{\mathrm{2}} +{x}−\mathrm{6}=\mathrm{0}\rightarrow\Delta=\mathrm{1}−\mathrm{4}\left(−\mathrm{6}\right)\:=\mathrm{25}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{5}}{\mathrm{2}}=\mathrm{2}\:\:{and}\: \\ $$$${x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{5}}{\mathrm{2}}\:=−\mathrm{3}\:\Rightarrow{I}\:=\int\:\:\:\frac{{dx}}{{x}\sqrt{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)}}\:\:{we}\:{do}\:{the}\:{changement} \\ $$$$\sqrt{{x}−\mathrm{2}}={t}\:\Rightarrow{x}−\mathrm{2}={t}^{\mathrm{2}} \:\Rightarrow{x}={t}^{\mathrm{2}} \:+\mathrm{2}\:\Rightarrow{I}\:=\int\:\:\:\frac{\mathrm{2}{tdt}}{\left({t}^{\mathrm{2}} \:+\mathrm{2}\right){t}\sqrt{{t}^{\mathrm{2}} +\mathrm{2}+\mathrm{3}}} \\ $$$$=\int\:\:\:\frac{\mathrm{2}{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} \:+\mathrm{5}}}\:\:{af}\:{ter}\:{we}\:{do}\:{the}\:{changement}\:{t}=\sqrt{\mathrm{5}}{sh}\left({u}\right)\:\Rightarrow \\ $$$${I}\:=\int\:\:\:\:\frac{\mathrm{2}\sqrt{\mathrm{5}}{ch}\left({u}\right)}{\left(\mathrm{25}{sh}^{\mathrm{2}} {u}\:+\mathrm{2}\right)\sqrt{\mathrm{5}}{ch}\left({u}\right)}{du}\:=\int\:\:\:\:\frac{\mathrm{2}{du}}{\mathrm{25}\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}}+\mathrm{2}} \\ $$$$=\int\:\:\:\:\:\frac{\mathrm{4}{du}}{\mathrm{25}{ch}\left(\mathrm{2}{u}\right)−\mathrm{25}+\mathrm{4}}\:=\int\:\:\:\frac{\mathrm{4}{du}}{\mathrm{25}{ch}\left(\mathrm{2}{u}\right)−\mathrm{21}} \\ $$$$=\int\:\:\:\frac{\mathrm{4}{du}}{\mathrm{25}\frac{{e}^{\mathrm{2}{u}} +{e}^{−\mathrm{2}{u}} }{\mathrm{2}}−\mathrm{21}}\:=\int\:\:\frac{\mathrm{4}{du}}{\mathrm{25}{e}^{\mathrm{2}{u}} +\mathrm{25}{e}^{−\mathrm{2}{u}} −\mathrm{42}} \\ $$$$=_{{e}^{\mathrm{2}{u}} ={t}} \:\:\:\:\int\:\:\:\frac{\mathrm{4}}{\mathrm{25}{t}+\mathrm{25}{t}^{−\mathrm{1}} −\mathrm{42}}×\frac{{dt}}{\mathrm{2}{t}}\:=\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{25}{t}^{\mathrm{2}} +\mathrm{25}}\:=\frac{\mathrm{2}}{\mathrm{25}}\:\int\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{25}}\:{arctan}\left({t}\right)+{c}\:=\frac{\mathrm{2}}{\mathrm{25}}\:{arctan}\left({e}^{\mathrm{2}{u}} \right)\:+{c} \\ $$$${but}\:{u}={argsh}\left(\frac{{t}}{\:\sqrt{\mathrm{5}}}\right)\:={ln}\left(\frac{{t}}{\:\sqrt{\mathrm{5}}}+\sqrt{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{\mathrm{5}}}\right)\:\Rightarrow\: \\ $$$${e}^{\mathrm{2}{u}} =\left(\frac{{t}}{\:\sqrt{\mathrm{5}}}+\sqrt{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{\mathrm{5}}}\right)^{\mathrm{2}} \:\Rightarrow\:{I}\:=\frac{\mathrm{2}}{\mathrm{25}}\:{arctan}\left\{\left(\frac{{t}+\sqrt{\mathrm{5}+{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \right\}\:+{C} \\ $$
Answered by MJS last updated on 02/Sep/19
∫(dx/(x(√(x^2 +x−6))))= [t=((12−x)/(5x)) → dx=−((5x^2 )/(12))dt] =−((√6)/6)∫(dt/( (√(1−t^2 ))))=−((√6)/6)arcsin t = =((√6)/6)arcsin ((x−12)/(5x))
$$\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}−\mathrm{6}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{12}−{x}}{\mathrm{5}{x}}\:\rightarrow\:{dx}=−\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{12}}{dt}\right] \\ $$$$=−\frac{\sqrt{\mathrm{6}}}{\mathrm{6}}\int\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=−\frac{\sqrt{\mathrm{6}}}{\mathrm{6}}\mathrm{arcsin}\:{t}\:= \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{6}}\mathrm{arcsin}\:\frac{{x}−\mathrm{12}}{\mathrm{5}{x}} \\ $$
Commented by MJS last updated on 02/Sep/19
∫(dx/(x(√((x+a^2 )(x−b^2 )))))= [t=(((a^2 −b^2 )x−2a^2 b^2 )/((a^2 +b^2 )x)) → dx=(((a^2 +b^2 )x^2 )/(2a^2 b^2 ))dt] =−(1/( (√(a^2 b^2 ))))∫(dt/( (√(1−t^2 ))))
$$\int\frac{{dx}}{{x}\sqrt{\left({x}+{a}^{\mathrm{2}} \right)\left({x}−{b}^{\mathrm{2}} \right)}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){x}−\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){x}}\:\rightarrow\:{dx}=\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} }{\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}\int\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *