Menu Close

Question-6791

Tinku Tara 0 Comments
Pin




Question Number 6791 by Tawakalitu. last updated on 26/Jul/16
Commented by Yozzii last updated on 27/Jul/16
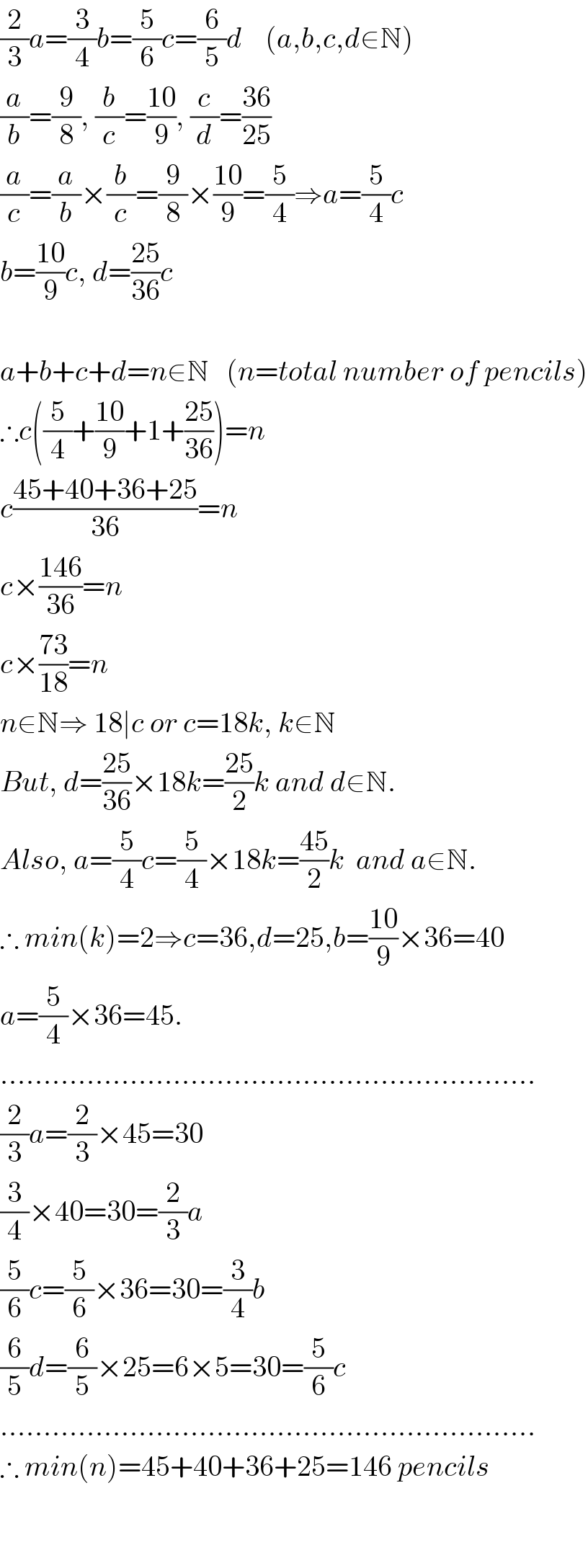
(2/3)a=(3/4)b=(5/6)c=(6/5)d (a,b,c,d∈N) (a/b)=(9/8), (b/c)=((10)/9), (c/d)=((36)/(25)) (a/c)=(a/b)×(b/c)=(9/8)×((10)/9)=(5/4)⇒a=(5/4)c b=((10)/9)c, d=((25)/(36))c a+b+c+d=n∈N (n=total number of pencils) ∴c((5/4)+((10)/9)+1+((25)/(36)))=n c((45+40+36+25)/(36))=n c×((146)/(36))=n c×((73)/(18))=n n∈N⇒ 18∣c or c=18k, k∈N But, d=((25)/(36))×18k=((25)/2)k and d∈N. Also, a=(5/4)c=(5/4)×18k=((45)/2)k and a∈N. ∴ min(k)=2⇒c=36,d=25,b=((10)/9)×36=40 a=(5/4)×36=45. .............................................................. (2/3)a=(2/3)×45=30 (3/4)×40=30=(2/3)a (5/6)c=(5/6)×36=30=(3/4)b (6/5)d=(6/5)×25=6×5=30=(5/6)c .............................................................. ∴ min(n)=45+40+36+25=146 pencils
$$\frac{\mathrm{2}}{\mathrm{3}}{a}=\frac{\mathrm{3}}{\mathrm{4}}{b}=\frac{\mathrm{5}}{\mathrm{6}}{c}=\frac{\mathrm{6}}{\mathrm{5}}{d}\:\:\:\:\left({a},{b},{c},{d}\in\mathbb{N}\right) \\ $$$$\frac{{a}}{{b}}=\frac{\mathrm{9}}{\mathrm{8}},\:\frac{{b}}{{c}}=\frac{\mathrm{10}}{\mathrm{9}},\:\frac{{c}}{{d}}=\frac{\mathrm{36}}{\mathrm{25}} \\ $$$$\frac{{a}}{{c}}=\frac{{a}}{{b}}×\frac{{b}}{{c}}=\frac{\mathrm{9}}{\mathrm{8}}×\frac{\mathrm{10}}{\mathrm{9}}=\frac{\mathrm{5}}{\mathrm{4}}\Rightarrow{a}=\frac{\mathrm{5}}{\mathrm{4}}{c} \\ $$$${b}=\frac{\mathrm{10}}{\mathrm{9}}{c},\:{d}=\frac{\mathrm{25}}{\mathrm{36}}{c} \\ $$$$ \\ $$$${a}+{b}+{c}+{d}={n}\in\mathbb{N}\:\:\:\left({n}={total}\:{number}\:{of}\:{pencils}\right) \\ $$$$\therefore{c}\left(\frac{\mathrm{5}}{\mathrm{4}}+\frac{\mathrm{10}}{\mathrm{9}}+\mathrm{1}+\frac{\mathrm{25}}{\mathrm{36}}\right)={n} \\ $$$${c}\frac{\mathrm{45}+\mathrm{40}+\mathrm{36}+\mathrm{25}}{\mathrm{36}}={n} \\ $$$${c}×\frac{\mathrm{146}}{\mathrm{36}}={n} \\ $$$${c}×\frac{\mathrm{73}}{\mathrm{18}}={n} \\ $$$${n}\in\mathbb{N}\Rightarrow\:\mathrm{18}\mid{c}\:{or}\:{c}=\mathrm{18}{k},\:{k}\in\mathbb{N} \\ $$$${But},\:{d}=\frac{\mathrm{25}}{\mathrm{36}}×\mathrm{18}{k}=\frac{\mathrm{25}}{\mathrm{2}}{k}\:{and}\:{d}\in\mathbb{N}. \\ $$$${Also},\:{a}=\frac{\mathrm{5}}{\mathrm{4}}{c}=\frac{\mathrm{5}}{\mathrm{4}}×\mathrm{18}{k}=\frac{\mathrm{45}}{\mathrm{2}}{k}\:\:{and}\:{a}\in\mathbb{N}. \\ $$$$\therefore\:{min}\left({k}\right)=\mathrm{2}\Rightarrow{c}=\mathrm{36},{d}=\mathrm{25},{b}=\frac{\mathrm{10}}{\mathrm{9}}×\mathrm{36}=\mathrm{40} \\ $$$${a}=\frac{\mathrm{5}}{\mathrm{4}}×\mathrm{36}=\mathrm{45}. \\ $$$$…………………………………………………….. \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{a}=\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{45}=\mathrm{30} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{40}=\mathrm{30}=\frac{\mathrm{2}}{\mathrm{3}}{a} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}}{c}=\frac{\mathrm{5}}{\mathrm{6}}×\mathrm{36}=\mathrm{30}=\frac{\mathrm{3}}{\mathrm{4}}{b} \\ $$$$\frac{\mathrm{6}}{\mathrm{5}}{d}=\frac{\mathrm{6}}{\mathrm{5}}×\mathrm{25}=\mathrm{6}×\mathrm{5}=\mathrm{30}=\frac{\mathrm{5}}{\mathrm{6}}{c} \\ $$$$…………………………………………………….. \\ $$$$\therefore\:{min}\left({n}\right)=\mathrm{45}+\mathrm{40}+\mathrm{36}+\mathrm{25}=\mathrm{146}\:{pencils} \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 27/Jul/16
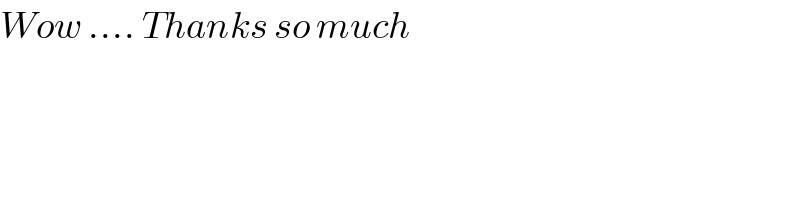
Wow .... Thanks so much
$${Wow}\:….\:{Thanks}\:{so}\:{much} \\ $$
Answered by Rasheed Soomro last updated on 27/Jul/16
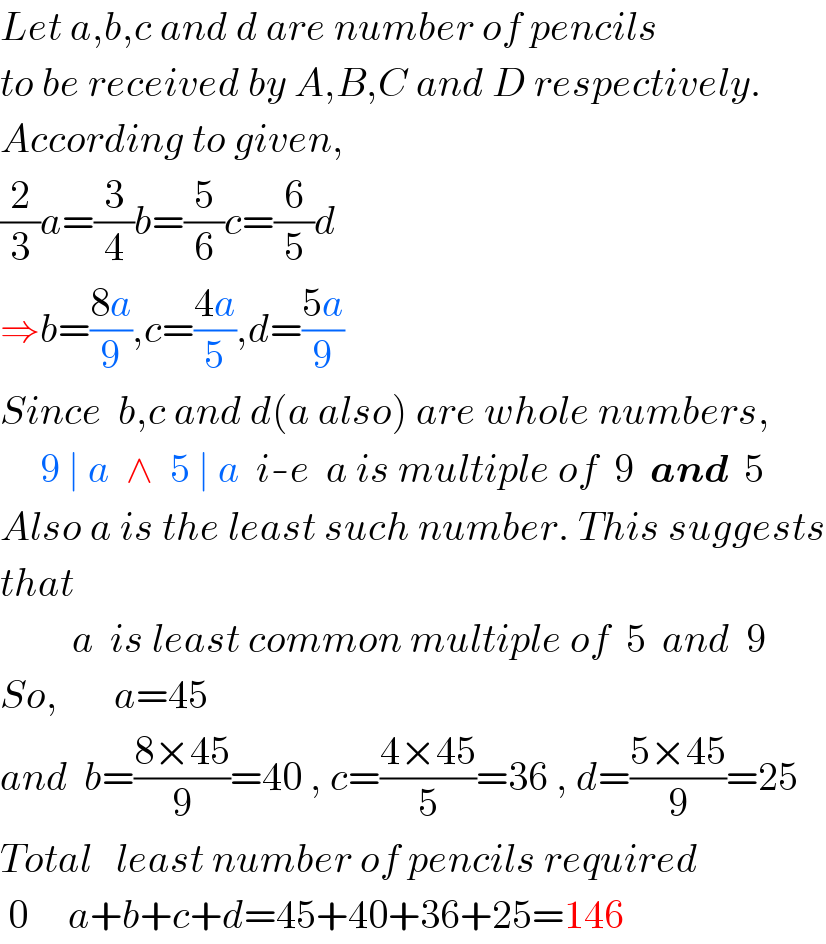
Let a,b,c and d are number of pencils to be received by A,B,C and D respectively. According to given, (2/3)a=(3/4)b=(5/6)c=(6/5)d ⇒b=((8a)/9),c=((4a)/5),d=((5a)/9) Since b,c and d(a also) are whole numbers, 9 ∣ a ∧ 5 ∣ a i-e a is multiple of 9 and 5 Also a is the least such number. This suggests that a is least common multiple of 5 and 9 So, a=45 and b=((8×45)/9)=40 , c=((4×45)/5)=36 , d=((5×45)/9)=25 Total least number of pencils required 0 a+b+c+d=45+40+36+25=146
$${Let}\:{a},{b},{c}\:{and}\:{d}\:{are}\:{number}\:{of}\:{pencils}\: \\ $$$${to}\:{be}\:{received}\:{by}\:{A},{B},{C}\:{and}\:{D}\:{respectively}. \\ $$$${According}\:{to}\:{given}, \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{a}=\frac{\mathrm{3}}{\mathrm{4}}{b}=\frac{\mathrm{5}}{\mathrm{6}}{c}=\frac{\mathrm{6}}{\mathrm{5}}{d} \\ $$$$\Rightarrow{b}=\frac{\mathrm{8}{a}}{\mathrm{9}},{c}=\frac{\mathrm{4}{a}}{\mathrm{5}},{d}=\frac{\mathrm{5}{a}}{\mathrm{9}} \\ $$$${Since}\:\:{b},{c}\:{and}\:{d}\left({a}\:{also}\right)\:{are}\:{whole}\:{numbers}, \\ $$$$\:\:\:\:\:\mathrm{9}\:\mid\:{a}\:\:\wedge\:\:\mathrm{5}\:\mid\:{a}\:\:{i}-{e}\:\:{a}\:{is}\:{multiple}\:{of}\:\:\mathrm{9}\:\:\boldsymbol{{and}}\:\:\mathrm{5} \\ $$$${Also}\:{a}\:{is}\:{the}\:{least}\:{such}\:{number}.\:{This}\:{suggests} \\ $$$${that}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:{a}\:\:{is}\:{least}\:{common}\:{multiple}\:{of}\:\:\mathrm{5}\:\:{and}\:\:\mathrm{9} \\ $$$${So},\:\:\:\:\:\:\:{a}=\mathrm{45} \\ $$$${and}\:\:{b}=\frac{\mathrm{8}×\mathrm{45}}{\mathrm{9}}=\mathrm{40}\:,\:{c}=\frac{\mathrm{4}×\mathrm{45}}{\mathrm{5}}=\mathrm{36}\:,\:{d}=\frac{\mathrm{5}×\mathrm{45}}{\mathrm{9}}=\mathrm{25} \\ $$$${Total}\:\:\:{least}\:{number}\:{of}\:{pencils}\:{required} \\ $$$$\:\mathrm{0}\:\:\:\:\:{a}+{b}+{c}+{d}=\mathrm{45}+\mathrm{40}+\mathrm{36}+\mathrm{25}=\mathrm{146} \\ $$
Commented by Tawakalitu. last updated on 27/Jul/16
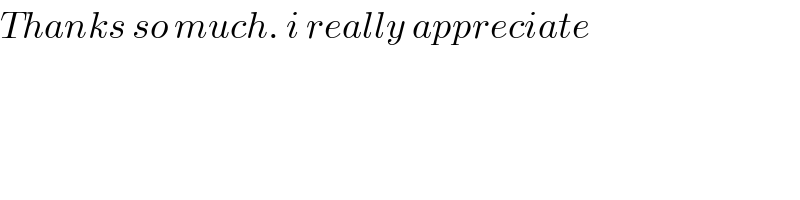
Thanks so much. i really appreciate
$${Thanks}\:{so}\:{much}.\:{i}\:{really}\:{appreciate} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *