Question Number 67937 by A8;15: last updated on 02/Sep/19
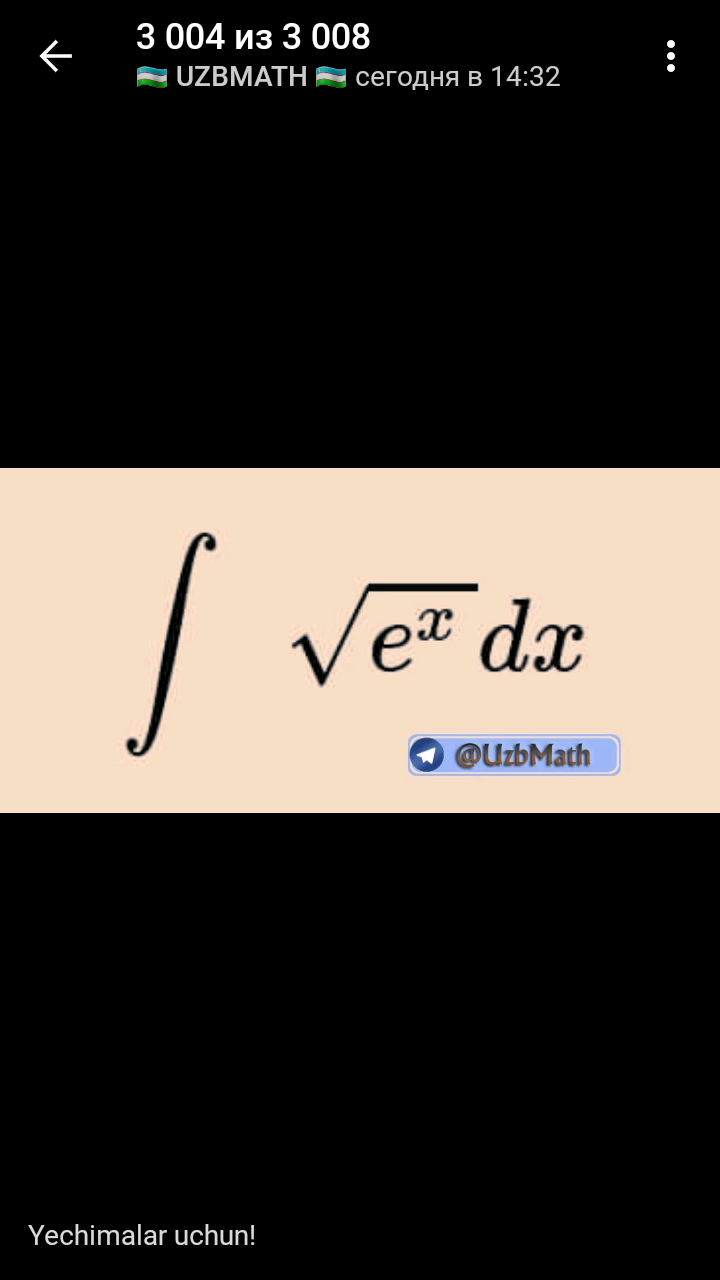
Commented by mathmax by abdo last updated on 02/Sep/19
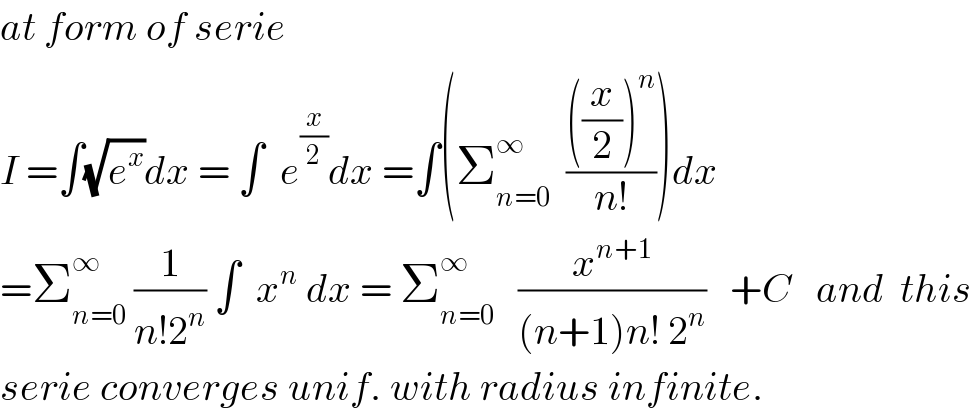
$${at}\:{form}\:{of}\:{serie} \\ $$$${I}\:=\int\sqrt{{e}^{{x}} }{dx}\:=\:\int\:\:{e}^{\frac{{x}}{\mathrm{2}}} {dx}\:=\int\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(\frac{{x}}{\mathrm{2}}\right)^{{n}} }{{n}!}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!\mathrm{2}^{{n}} }\:\int\:\:{x}^{{n}} \:{dx}\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right){n}!\:\mathrm{2}^{{n}} }\:\:\:+{C}\:\:\:{and}\:\:{this} \\ $$$${serie}\:{converges}\:{unif}.\:{with}\:{radius}\:{infinite}. \\ $$
