Question Number 67939 by ramirez105 last updated on 02/Sep/19
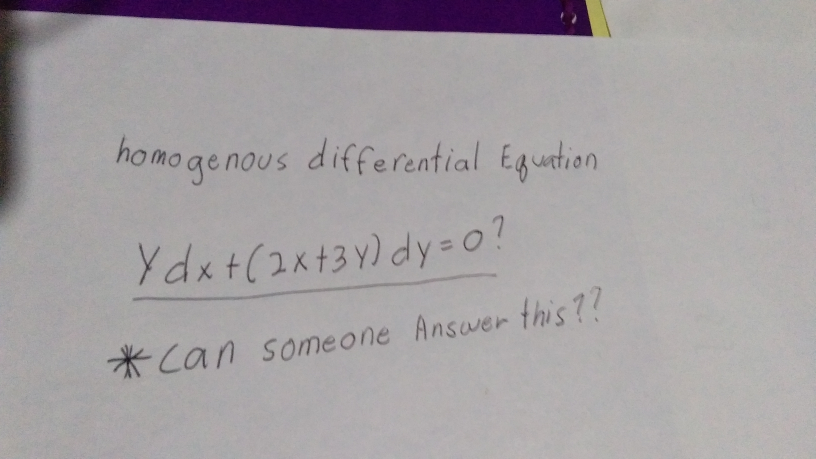
Commented by mr W last updated on 02/Sep/19
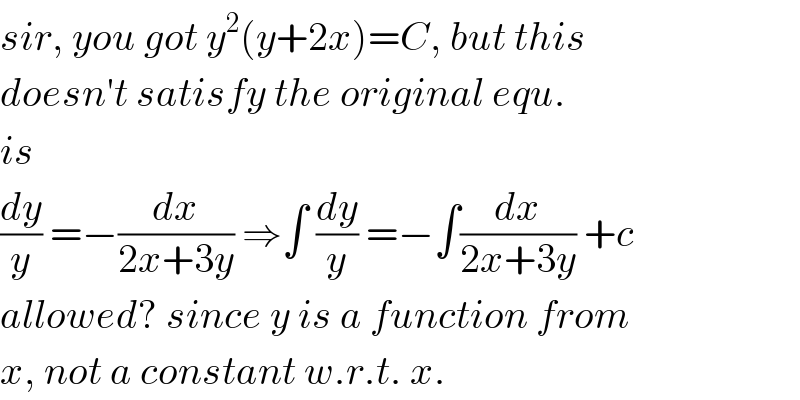
$${sir},\:{you}\:{got}\:{y}^{\mathrm{2}} \left({y}+\mathrm{2}{x}\right)={C},\:{but}\:{this} \\ $$$${doesn}'{t}\:{satisfy}\:{the}\:{original}\:{equ}. \\ $$$${is}\: \\ $$$$\frac{{dy}}{{y}}\:=−\frac{{dx}}{\mathrm{2}{x}+\mathrm{3}{y}}\:\Rightarrow\int\:\frac{{dy}}{{y}}\:=−\int\frac{{dx}}{\mathrm{2}{x}+\mathrm{3}{y}}\:+{c} \\ $$$${allowed}?\:{since}\:{y}\:{is}\:{a}\:{function}\:{from} \\ $$$${x},\:{not}\:{a}\:{constant}\:{w}.{r}.{t}.\:{x}. \\ $$
Commented by mathmax by abdo last updated on 02/Sep/19
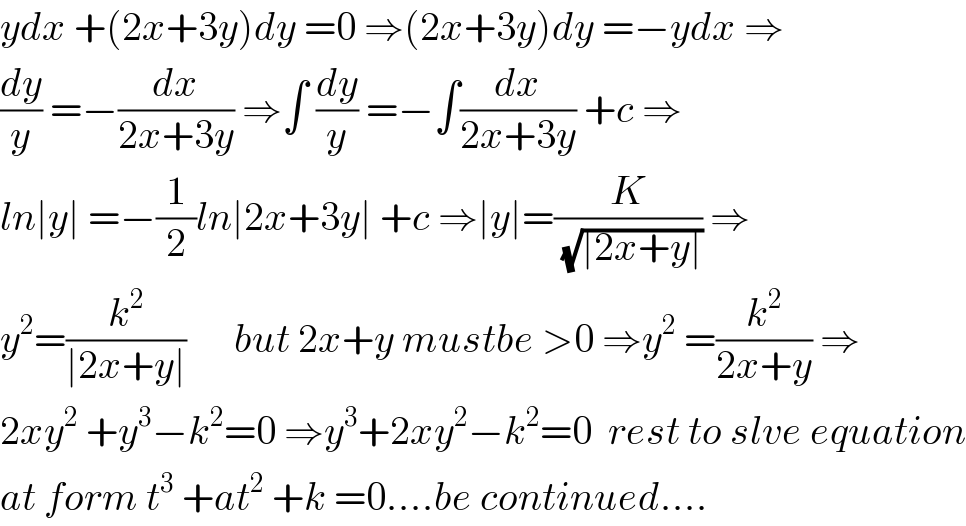
$${ydx}\:+\left(\mathrm{2}{x}+\mathrm{3}{y}\right){dy}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{2}{x}+\mathrm{3}{y}\right){dy}\:=−{ydx}\:\Rightarrow \\ $$$$\frac{{dy}}{{y}}\:=−\frac{{dx}}{\mathrm{2}{x}+\mathrm{3}{y}}\:\Rightarrow\int\:\frac{{dy}}{{y}}\:=−\int\frac{{dx}}{\mathrm{2}{x}+\mathrm{3}{y}}\:+{c}\:\Rightarrow \\ $$$${ln}\mid{y}\mid\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{2}{x}+\mathrm{3}{y}\mid\:+{c}\:\Rightarrow\mid{y}\mid=\frac{{K}}{\:\sqrt{\mid\mathrm{2}{x}+{y}\mid}}\:\Rightarrow \\ $$$${y}^{\mathrm{2}} =\frac{{k}^{\mathrm{2}} }{\mid\mathrm{2}{x}+{y}\mid}\:\:\:\:\:\:{but}\:\mathrm{2}{x}+{y}\:{mustbe}\:>\mathrm{0}\:\Rightarrow{y}^{\mathrm{2}} \:=\frac{{k}^{\mathrm{2}} }{\mathrm{2}{x}+{y}}\:\Rightarrow \\ $$$$\mathrm{2}{xy}^{\mathrm{2}} \:+{y}^{\mathrm{3}} −{k}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow{y}^{\mathrm{3}} +\mathrm{2}{xy}^{\mathrm{2}} −{k}^{\mathrm{2}} =\mathrm{0}\:\:{rest}\:{to}\:{slve}\:{equation} \\ $$$${at}\:{form}\:{t}^{\mathrm{3}} \:+{at}^{\mathrm{2}} \:+{k}\:=\mathrm{0}….{be}\:{continued}…. \\ $$
Answered by mr W last updated on 02/Sep/19
![ydx+(2x+3y)dy=0 y+(2x+3y)(dy/dx)=0 (y/x)+(2+3(y/x))(dy/dx)=0 let y=tx (dy/dx)=t+x(dt/dx) t+(2+3t)(t+x(dt/dx))=0 t+2t+3t^2 +x(2+3t)(dt/dx)=0 x(2+3t)(dt/dx)=−3t(t+1) ((2+3t)/(t(t+1)))dt=−((3dx)/x) ∫((2+3t)/(t(t+1)))dt=−3∫(dx/x) ∫[(2/t)+(1/(t+1))]dt=−3∫(dx/x) 2ln t+ln (t+1)=−3ln x+c ln t^2 (t+1)x^3 =c ⇒t^2 (t+1)x^3 =C ⇒y^2 (y+x)=C check: 2yy′(y+x)+y^2 (y′+1)=0 (3y^2 +2xy)y′+y^2 =0 (3y+2x)y′+y=0 ⇒(3y+2x)dy+ydx=0](https://www.tinkutara.com/question/Q67947.png)
$${ydx}+\left(\mathrm{2}{x}+\mathrm{3}{y}\right){dy}=\mathrm{0} \\ $$$${y}+\left(\mathrm{2}{x}+\mathrm{3}{y}\right)\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{y}}{{x}}+\left(\mathrm{2}+\mathrm{3}\frac{{y}}{{x}}\right)\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$${let}\:{y}={tx} \\ $$$$\frac{{dy}}{{dx}}={t}+{x}\frac{{dt}}{{dx}} \\ $$$${t}+\left(\mathrm{2}+\mathrm{3}{t}\right)\left({t}+{x}\frac{{dt}}{{dx}}\right)=\mathrm{0} \\ $$$${t}+\mathrm{2}{t}+\mathrm{3}{t}^{\mathrm{2}} +{x}\left(\mathrm{2}+\mathrm{3}{t}\right)\frac{{dt}}{{dx}}=\mathrm{0} \\ $$$${x}\left(\mathrm{2}+\mathrm{3}{t}\right)\frac{{dt}}{{dx}}=−\mathrm{3}{t}\left({t}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{2}+\mathrm{3}{t}}{{t}\left({t}+\mathrm{1}\right)}{dt}=−\frac{\mathrm{3}{dx}}{{x}} \\ $$$$\int\frac{\mathrm{2}+\mathrm{3}{t}}{{t}\left({t}+\mathrm{1}\right)}{dt}=−\mathrm{3}\int\frac{{dx}}{{x}} \\ $$$$\int\left[\frac{\mathrm{2}}{{t}}+\frac{\mathrm{1}}{{t}+\mathrm{1}}\right]{dt}=−\mathrm{3}\int\frac{{dx}}{{x}} \\ $$$$\mathrm{2ln}\:{t}+\mathrm{ln}\:\left({t}+\mathrm{1}\right)=−\mathrm{3ln}\:{x}+{c} \\ $$$$\mathrm{ln}\:{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right){x}^{\mathrm{3}} ={c} \\ $$$$\Rightarrow{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right){x}^{\mathrm{3}} ={C} \\ $$$$\Rightarrow{y}^{\mathrm{2}} \left({y}+{x}\right)={C} \\ $$$${check}: \\ $$$$\mathrm{2}{yy}'\left({y}+{x}\right)+{y}^{\mathrm{2}} \left({y}'+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{3}{y}^{\mathrm{2}} +\mathrm{2}{xy}\right){y}'+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{3}{y}+\mathrm{2}{x}\right){y}'+{y}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{3}{y}+\mathrm{2}{x}\right){dy}+{ydx}=\mathrm{0} \\ $$
