Question Number 67983 by peter frank last updated on 03/Sep/19

Commented by Abdo msup. last updated on 03/Sep/19
![b) let f(x)=((1/x))^(x ) ⇒f(x)=x^(−x) =e^(−xln(x)) f is?defined on ]0,+∞[ lim_(x→0 and x>0) f(x)=e^(0=1) lim_(x→+∞) f(x) =lim_(x→+∞) e^(−xlnx) =0 f^′ (x)= (−lnx−1)e^(−xlnx) =−(lnx+1)f(x) f^′ (x) =0 ⇔lnx+1=0 ⇔lnx =−1 ⇔x=e^(−1) (see thst f)x>0 ) f(e^(−1) ) =e^(−e^(−1) ln(e^(−1) )) =e^(1/e) f^′ (x)>0 ⇔ lnx +1<0 ⇔lnx<−1 ⇔x<e^(−1) varistion of f x 0 e^(−1) +∞ f^′ (x) + 0 − f(x) 1 incr e^(1/e) dcres 0 ⇒ max f(x)_(x>0) =f(e^(−1) ) = e^(1/e)](https://www.tinkutara.com/question/Q67984.png)
$$\left.{b}\right)\:{let}\:{f}\left({x}\right)=\left(\frac{\mathrm{1}}{{x}}\right)^{{x}\:} \:\Rightarrow{f}\left({x}\right)={x}^{−{x}} \:={e}^{−{xln}\left({x}\right)} \\ $$$$\left.{f}\:{is}?{defined}\:{on}\:\right]\mathrm{0},+\infty\left[\right. \\ $$$${lim}_{{x}\rightarrow\mathrm{0}\:{and}\:{x}>\mathrm{0}} \:\:\:{f}\left({x}\right)={e}^{\mathrm{0}=\mathrm{1}} \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)\:={lim}_{{x}\rightarrow+\infty} \:\:\:{e}^{−{xlnx}} =\mathrm{0} \\ $$$${f}^{'} \left({x}\right)=\:\left(−{lnx}−\mathrm{1}\right){e}^{−{xlnx}} \:=−\left({lnx}+\mathrm{1}\right){f}\left({x}\right) \\ $$$${f}^{'} \left({x}\right)\:=\mathrm{0}\:\:\Leftrightarrow{lnx}+\mathrm{1}=\mathrm{0}\:\:\Leftrightarrow{lnx}\:=−\mathrm{1}\:\Leftrightarrow{x}={e}^{−\mathrm{1}} \\ $$$$\left.\left({see}\:{thst}\:{f}\right){x}>\mathrm{0}\:\right) \\ $$$${f}\left({e}^{−\mathrm{1}} \right)\:={e}^{−{e}^{−\mathrm{1}} {ln}\left({e}^{−\mathrm{1}} \right)} \:={e}^{\frac{\mathrm{1}}{{e}}} \\ $$$${f}^{'} \left({x}\right)>\mathrm{0}\:\Leftrightarrow\:{lnx}\:+\mathrm{1}<\mathrm{0}\:\Leftrightarrow{lnx}<−\mathrm{1}\:\Leftrightarrow{x}<{e}^{−\mathrm{1}} \\ $$$${varistion}\:{of}\:{f} \\ $$$${x}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{e}^{−\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${f}^{'} \left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:− \\ $$$${f}\left({x}\right)\:\:\:\:\mathrm{1}\:{incr}\:\:\:\:\:\:\:{e}^{\frac{\mathrm{1}}{{e}}} \:\:\:\:\:\:\:\:{dcres}\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\Rightarrow\:{max}\:{f}\left({x}\right)_{{x}>\mathrm{0}} \:\:\:\:={f}\left({e}^{−\mathrm{1}} \right)\:=\:{e}^{\frac{\mathrm{1}}{{e}}} \\ $$
Answered by MJS last updated on 03/Sep/19

$$\left.{a}\right)\:\mathrm{geometrically}: \\ $$$$\mathrm{any}\:\mathrm{rectangular}\:\mathrm{triangle}\:\mathrm{is}\:\mathrm{one}\:\mathrm{half}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{rectangle},\:\mathrm{the}\:\mathrm{hypothenuse}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$\mathrm{is}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{diagonals}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle},\:\mathrm{the} \\ $$$$\mathrm{diagonals}\:\mathrm{bisect}\:\mathrm{each}\:\mathrm{other},\:\mathrm{the}\:\mathrm{rectangle}'\mathrm{s} \\ $$$$\mathrm{circumcircle}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{triangle}'\mathrm{s}, \\ $$$$\mathrm{done} \\ $$
Commented by peter frank last updated on 03/Sep/19

$${thanks}\: \\ $$
Answered by MJS last updated on 03/Sep/19
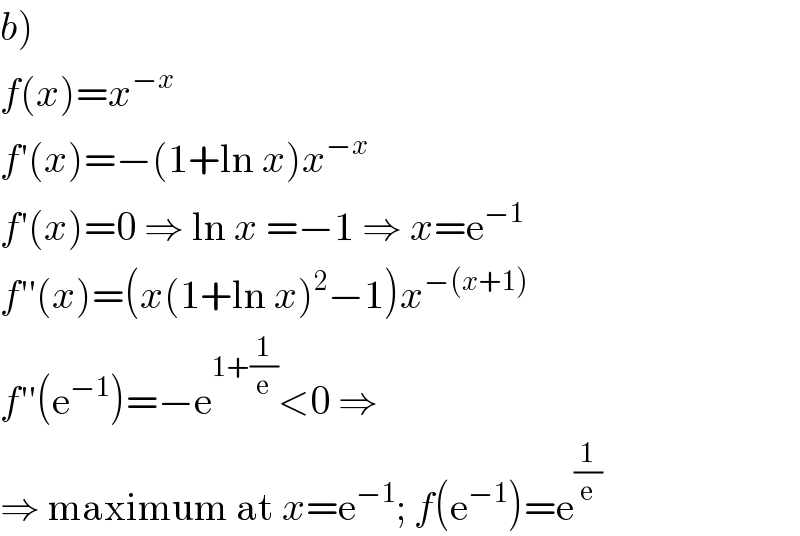
$$\left.{b}\right) \\ $$$${f}\left({x}\right)={x}^{−{x}} \\ $$$${f}'\left({x}\right)=−\left(\mathrm{1}+\mathrm{ln}\:{x}\right){x}^{−{x}} \\ $$$${f}'\left({x}\right)=\mathrm{0}\:\Rightarrow\:\mathrm{ln}\:{x}\:=−\mathrm{1}\:\Rightarrow\:{x}=\mathrm{e}^{−\mathrm{1}} \\ $$$${f}''\left({x}\right)=\left({x}\left(\mathrm{1}+\mathrm{ln}\:{x}\right)^{\mathrm{2}} −\mathrm{1}\right){x}^{−\left({x}+\mathrm{1}\right)} \\ $$$${f}''\left(\mathrm{e}^{−\mathrm{1}} \right)=−\mathrm{e}^{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{e}}} <\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{maximum}\:\mathrm{at}\:{x}=\mathrm{e}^{−\mathrm{1}} ;\:{f}\left(\mathrm{e}^{−\mathrm{1}} \right)=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{e}}} \\ $$
Commented by peter frank last updated on 03/Sep/19

$${thank}\:{you} \\ $$
