Menu Close

Question-67991

Tinku Tara 0 Comments
Pin




Question Number 67991 by ramirez105 last updated on 03/Sep/19
Commented by mathmax by abdo last updated on 03/Sep/19
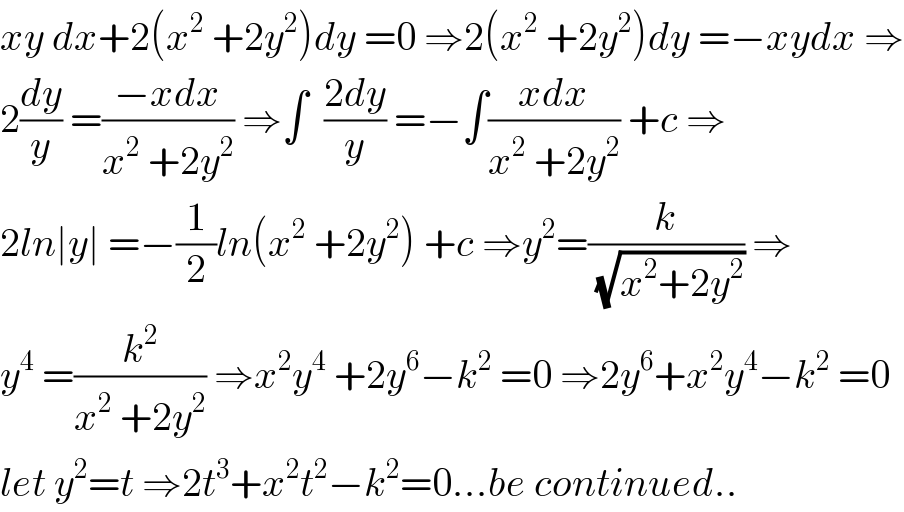
xy dx+2(x^2 +2y^2 )dy =0 ⇒2(x^2 +2y^2 )dy =−xydx ⇒ 2(dy/y) =((−xdx)/(x^2 +2y^2 )) ⇒∫ ((2dy)/y) =−∫((xdx)/(x^2 +2y^2 )) +c ⇒ 2ln∣y∣ =−(1/2)ln(x^2 +2y^2 ) +c ⇒y^2 =(k/( (√(x^2 +2y^2 )))) ⇒ y^4 =(k^2 /(x^2 +2y^2 )) ⇒x^2 y^4 +2y^6 −k^2 =0 ⇒2y^6 +x^2 y^4 −k^2 =0 let y^2 =t ⇒2t^3 +x^2 t^2 −k^2 =0...be continued..
$${xy}\:{dx}+\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \right){dy}\:=\mathrm{0}\:\Rightarrow\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \right){dy}\:=−{xydx}\:\Rightarrow \\ $$$$\mathrm{2}\frac{{dy}}{{y}}\:=\frac{−{xdx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} }\:\Rightarrow\int\:\:\frac{\mathrm{2}{dy}}{{y}}\:=−\int\frac{{xdx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} }\:+{c}\:\Rightarrow \\ $$$$\mathrm{2}{ln}\mid{y}\mid\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \right)\:+{c}\:\Rightarrow{y}^{\mathrm{2}} =\frac{{k}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${y}^{\mathrm{4}} \:=\frac{{k}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} }\:\Rightarrow{x}^{\mathrm{2}} {y}^{\mathrm{4}} \:+\mathrm{2}{y}^{\mathrm{6}} −{k}^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{2}{y}^{\mathrm{6}} +{x}^{\mathrm{2}} {y}^{\mathrm{4}} −{k}^{\mathrm{2}} \:=\mathrm{0} \\ $$$${let}\:{y}^{\mathrm{2}} ={t}\:\Rightarrow\mathrm{2}{t}^{\mathrm{3}} +{x}^{\mathrm{2}} {t}^{\mathrm{2}} −{k}^{\mathrm{2}} =\mathrm{0}…{be}\:{continued}.. \\ $$
Answered by Tanmay chaudhury last updated on 03/Sep/19
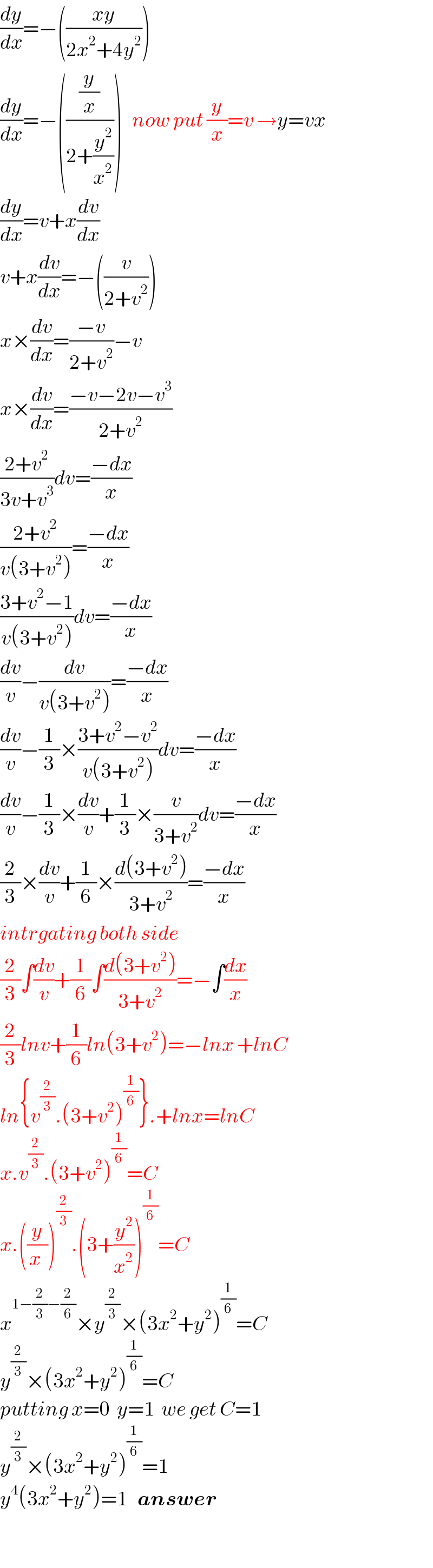
(dy/dx)=−(((xy)/(2x^2 +4y^2 ))) (dy/dx)=−(((y/x)/(2+(y^2 /x^2 )))) now put (y/x)=v →y=vx (dy/dx)=v+x(dv/dx) v+x(dv/dx)=−((v/(2+v^2 ))) x×(dv/dx)=((−v)/(2+v^2 ))−v x×(dv/dx)=((−v−2v−v^3 )/(2+v^2 )) ((2+v^2 )/(3v+v^3 ))dv=((−dx)/x) ((2+v^2 )/(v(3+v^2 )))=((−dx)/x) ((3+v^2 −1)/(v(3+v^2 )))dv=((−dx)/x) (dv/v)−(dv/(v(3+v^2 )))=((−dx)/x) (dv/v)−(1/3)×((3+v^2 −v^2 )/(v(3+v^2 )))dv=((−dx)/x) (dv/v)−(1/3)×(dv/v)+(1/3)×(v/(3+v^2 ))dv=((−dx)/x) (2/3)×(dv/v)+(1/6)×((d(3+v^2 ))/(3+v^2 ))=((−dx)/x) intrgating both side (2/3)∫(dv/v)+(1/6)∫((d(3+v^2 ))/(3+v^2 ))=−∫(dx/x) (2/3)lnv+(1/6)ln(3+v^2 )=−lnx +lnC ln{v^(2/3) .(3+v^2 )^(1/6) }.+lnx=lnC x.v^(2/3) .(3+v^2 )^(1/6) =C x.((y/(x )))^(2/3) .(3+(y^2 /x^2 ))^(1/6) =C x^(1−(2/3)−(2/6)) ×y^(2/3) ×(3x^2 +y^2 )^(1/6) =C y^(2/3) ×(3x^2 +y^2 )^(1/6) =C putting x=0 y=1 we get C=1 y^(2/3) ×(3x^2 +y^2 )^(1/6) =1 y^4 (3x^2 +y^2 )=1 answer
$$\frac{{dy}}{{dx}}=−\left(\frac{{xy}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} }\right) \\ $$$$\frac{{dy}}{{dx}}=−\left(\frac{\frac{{y}}{{x}}}{\mathrm{2}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}\right)\:\:\:{now}\:{put}\:\frac{{y}}{{x}}={v}\:\rightarrow{y}={vx} \\ $$$$\frac{{dy}}{{dx}}={v}+{x}\frac{{dv}}{{dx}} \\ $$$${v}+{x}\frac{{dv}}{{dx}}=−\left(\frac{{v}}{\mathrm{2}+{v}^{\mathrm{2}} }\right) \\ $$$${x}×\frac{{dv}}{{dx}}=\frac{−{v}}{\mathrm{2}+{v}^{\mathrm{2}} }−{v} \\ $$$${x}×\frac{{dv}}{{dx}}=\frac{−{v}−\mathrm{2}{v}−{v}^{\mathrm{3}} }{\mathrm{2}+{v}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}+{v}^{\mathrm{2}} }{\mathrm{3}{v}+{v}^{\mathrm{3}} }{dv}=\frac{−{dx}}{{x}} \\ $$$$\frac{\mathrm{2}+{v}^{\mathrm{2}} }{{v}\left(\mathrm{3}+{v}^{\mathrm{2}} \right)}=\frac{−{dx}}{{x}} \\ $$$$\frac{\mathrm{3}+{v}^{\mathrm{2}} −\mathrm{1}}{{v}\left(\mathrm{3}+{v}^{\mathrm{2}} \right)}{dv}=\frac{−{dx}}{{x}} \\ $$$$\frac{{dv}}{{v}}−\frac{{dv}}{{v}\left(\mathrm{3}+{v}^{\mathrm{2}} \right)}=\frac{−{dx}}{{x}} \\ $$$$\frac{{dv}}{{v}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}+{v}^{\mathrm{2}} −{v}^{\mathrm{2}} }{{v}\left(\mathrm{3}+{v}^{\mathrm{2}} \right)}{dv}=\frac{−{dx}}{{x}} \\ $$$$\frac{{dv}}{{v}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{{dv}}{{v}}+\frac{\mathrm{1}}{\mathrm{3}}×\frac{{v}}{\mathrm{3}+{v}^{\mathrm{2}} }{dv}=\frac{−{dx}}{{x}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}×\frac{{dv}}{{v}}+\frac{\mathrm{1}}{\mathrm{6}}×\frac{{d}\left(\mathrm{3}+{v}^{\mathrm{2}} \right)}{\mathrm{3}+{v}^{\mathrm{2}} }=\frac{−{dx}}{{x}} \\ $$$${intrgating}\:{both}\:{side} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dv}}{{v}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left(\mathrm{3}+{v}^{\mathrm{2}} \right)}{\mathrm{3}+{v}^{\mathrm{2}} }=−\int\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{lnv}+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\mathrm{3}+{v}^{\mathrm{2}} \right)=−{lnx}\:+{lnC} \\ $$$${ln}\left\{{v}^{\frac{\mathrm{2}}{\mathrm{3}}} .\left(\mathrm{3}+{v}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} \right\}.+{lnx}={lnC} \\ $$$${x}.{v}^{\frac{\mathrm{2}}{\mathrm{3}}} .\left(\mathrm{3}+{v}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} ={C} \\ $$$${x}.\left(\frac{{y}}{{x}\:}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} .\left(\mathrm{3}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{6}}} ={C} \\ $$$${x}^{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{6}}} ×{y}^{\frac{\mathrm{2}}{\mathrm{3}}} ×\left(\mathrm{3}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} ={C} \\ $$$${y}^{\frac{\mathrm{2}}{\mathrm{3}}} ×\left(\mathrm{3}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} ={C} \\ $$$${putting}\:{x}=\mathrm{0}\:\:{y}=\mathrm{1}\:\:{we}\:{get}\:{C}=\mathrm{1} \\ $$$${y}^{\frac{\mathrm{2}}{\mathrm{3}}} ×\left(\mathrm{3}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} =\mathrm{1} \\ $$$${y}^{\mathrm{4}} \left(\mathrm{3}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{1}\:\:\:\boldsymbol{{answer}} \\ $$$$ \\ $$
Commented by Prithwish sen last updated on 03/Sep/19
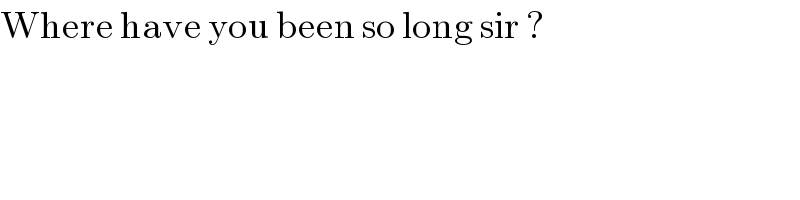
Where have you been so long sir ?
$$\mathrm{Where}\:\mathrm{have}\:\mathrm{you}\:\mathrm{been}\:\mathrm{so}\:\mathrm{long}\:\mathrm{sir}\:? \\ $$
Commented by peter frank last updated on 03/Sep/19
thank you
$${thank}\:{you} \\ $$$$ \\ $$
Commented by Tanmay chaudhury last updated on 03/Sep/19
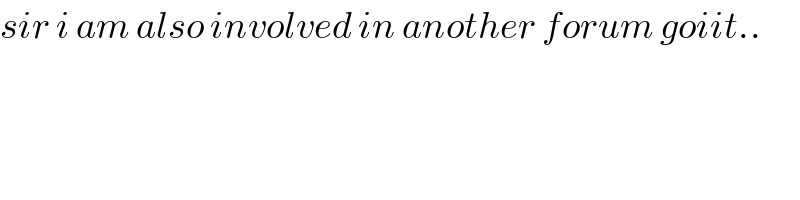
sir i am also involved in another forum goiit..
$${sir}\:{i}\:{am}\:{also}\:{involved}\:{in}\:{another}\:{forum}\:{goiit}.. \\ $$$$ \\ $$
Commented by mr W last updated on 03/Sep/19
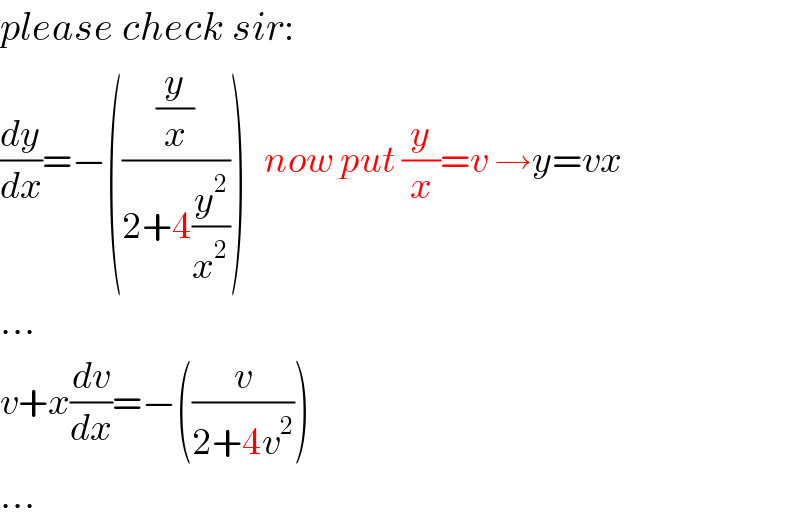
please check sir: (dy/dx)=−(((y/x)/(2+4(y^2 /x^2 )))) now put (y/x)=v →y=vx ... v+x(dv/dx)=−((v/(2+4v^2 ))) ...
$${please}\:{check}\:{sir}: \\ $$$$\frac{{dy}}{{dx}}=−\left(\frac{\frac{{y}}{{x}}}{\mathrm{2}+\mathrm{4}\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}\right)\:\:\:{now}\:{put}\:\frac{{y}}{{x}}={v}\:\rightarrow{y}={vx} \\ $$$$… \\ $$$${v}+{x}\frac{{dv}}{{dx}}=−\left(\frac{{v}}{\mathrm{2}+\mathrm{4}{v}^{\mathrm{2}} }\right) \\ $$$$… \\ $$
Commented by Tanmay chaudhury last updated on 03/Sep/19
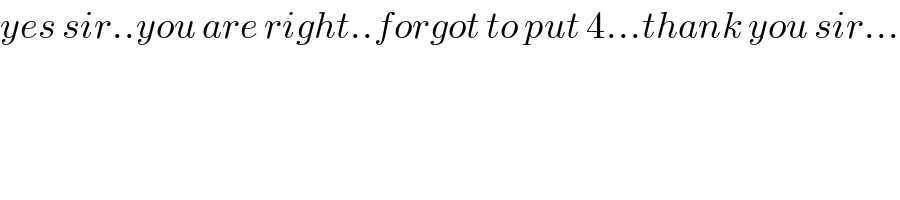
yes sir..you are right..forgot to put 4...thank you sir...
$${yes}\:{sir}..{you}\:{are}\:{right}..{forgot}\:{to}\:{put}\:\mathrm{4}…{thank}\:{you}\:{sir}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *