Question Number 68022 by anaplak last updated on 03/Sep/19
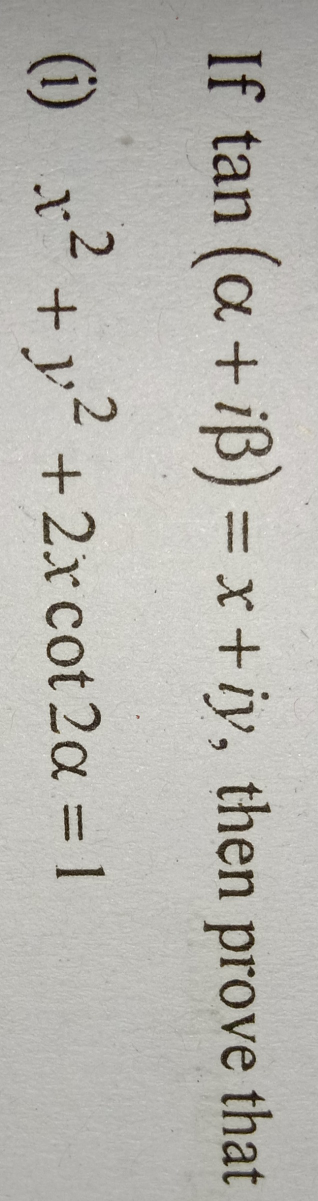
Commented by anaplak last updated on 08/Sep/19

$${your}\:{given}\:{solution}\:{is}\:{not}\:{right}\:{according}\:{to}\:{my}\:{question}\:.. \\ $$
Answered by mr W last updated on 03/Sep/19
![tan (α+βi)=x+yi ⇒((sin (2α)+i sinh (2β))/(cos (2α)+cosh (2β)))=x+yi ⇒x=((sin (2α))/(cos (2α)+cosh (2β))) ⇒y=((sinh (2β))/(cos (2α)+cosh (2β))) ⇒x^2 +y^2 +2xcot^(−1) 2α=((sin^2 (2α)+sinh^2 (2β)+2 cos (2α)[cos (2α)+cosh (2β)])/([cos (2α)+cosh (2β)]^2 )) ⇒x^2 +y^2 +2xcot^(−1) 2α=((1+sinh^2 (2β)+cos^2 (2α)+2cos (2α)cosh (2β))/([cos (2α)+cosh (2β)]^2 )) ⇒x^2 +y^2 +2xcot^(−1) 2α=((cosh^2 (2β)+cos^2 (2α)+2cos (2α)cosh (2β))/([cos (2α)+cosh (2β)]^2 )) ⇒x^2 +y^2 +2xcot^(−1) 2α=(([cos (2α)+cosh (2β)]^2 )/([cos (2α)+cosh (2β)]^2 )) ⇒x^2 +y^2 +2xcot^(−1) 2α=1](https://www.tinkutara.com/question/Q68024.png)
$$\mathrm{tan}\:\left(\alpha+\beta{i}\right)={x}+{yi} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\left(\mathrm{2}\alpha\right)+{i}\:\mathrm{sinh}\:\left(\mathrm{2}\beta\right)}{\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)}={x}+{yi} \\ $$$$\Rightarrow{x}=\frac{\mathrm{sin}\:\left(\mathrm{2}\alpha\right)}{\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)} \\ $$$$\Rightarrow{y}=\frac{\mathrm{sinh}\:\left(\mathrm{2}\beta\right)}{\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}\mathrm{cot}^{−\mathrm{1}} \mathrm{2}\alpha=\frac{\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}\alpha\right)+\mathrm{sinh}^{\mathrm{2}} \:\left(\mathrm{2}\beta\right)+\mathrm{2}\:\mathrm{cos}\:\left(\mathrm{2}\alpha\right)\left[\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)\right]}{\left[\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)\right]^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}\mathrm{cot}^{−\mathrm{1}} \mathrm{2}\alpha=\frac{\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} \:\left(\mathrm{2}\beta\right)+\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\alpha\right)+\mathrm{2cos}\:\left(\mathrm{2}\alpha\right)\mathrm{cosh}\:\left(\mathrm{2}\beta\right)}{\left[\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)\right]^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}\mathrm{cot}^{−\mathrm{1}} \mathrm{2}\alpha=\frac{\mathrm{cosh}^{\mathrm{2}} \:\left(\mathrm{2}\beta\right)+\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\alpha\right)+\mathrm{2cos}\:\left(\mathrm{2}\alpha\right)\mathrm{cosh}\:\left(\mathrm{2}\beta\right)}{\left[\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)\right]^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}\mathrm{cot}^{−\mathrm{1}} \mathrm{2}\alpha=\frac{\left[\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)\right]^{\mathrm{2}} }{\left[\mathrm{cos}\:\left(\mathrm{2}\alpha\right)+\mathrm{cosh}\:\left(\mathrm{2}\beta\right)\right]^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}\mathrm{cot}^{−\mathrm{1}} \mathrm{2}\alpha=\mathrm{1} \\ $$
