Question Number 68046 by mhmd last updated on 03/Sep/19

Answered by mind is power last updated on 03/Sep/19
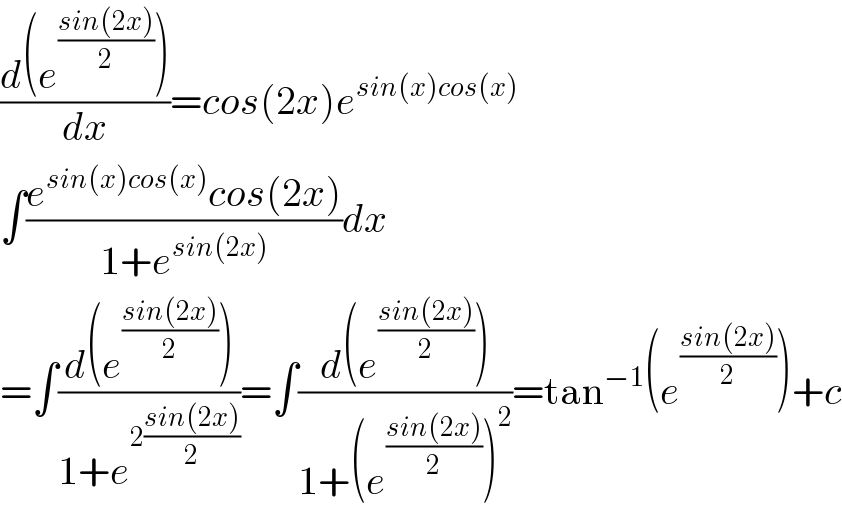
$$\frac{{d}\left({e}^{\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \right)}{{dx}}={cos}\left(\mathrm{2}{x}\right){e}^{{sin}\left({x}\right){cos}\left({x}\right)} \\ $$$$\int\frac{{e}^{{sin}\left({x}\right){cos}\left({x}\right)} {cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{e}^{{sin}\left(\mathrm{2}{x}\right)} }{dx} \\ $$$$=\int\frac{{d}\left({e}^{\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \right)}{\mathrm{1}+{e}^{\mathrm{2}\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} }=\int\frac{{d}\left({e}^{\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \right)}{\mathrm{1}+\left({e}^{\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \right)^{\mathrm{2}} }=\mathrm{tan}^{−\mathrm{1}} \left({e}^{\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \right)+{c} \\ $$
