Question Number 68078 by anaplak last updated on 04/Sep/19

Answered by Smail last updated on 04/Sep/19
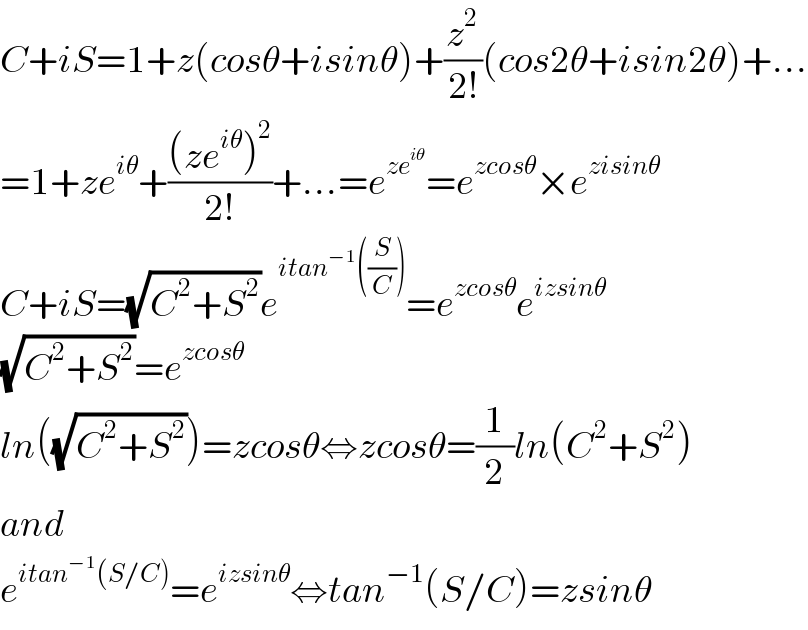
$${C}+{iS}=\mathrm{1}+{z}\left({cos}\theta+{isin}\theta\right)+\frac{{z}^{\mathrm{2}} }{\mathrm{2}!}\left({cos}\mathrm{2}\theta+{isin}\mathrm{2}\theta\right)+… \\ $$$$=\mathrm{1}+{ze}^{{i}\theta} +\frac{\left({ze}^{{i}\theta} \right)^{\mathrm{2}} }{\mathrm{2}!}+…={e}^{{ze}^{{i}\theta} } ={e}^{{zcos}\theta} ×{e}^{{zisin}\theta} \\ $$$${C}+{iS}=\sqrt{{C}^{\mathrm{2}} +{S}^{\mathrm{2}} }{e}^{{itan}^{−\mathrm{1}} \left(\frac{{S}}{{C}}\right)} ={e}^{{zcos}\theta} {e}^{{izsin}\theta} \\ $$$$\sqrt{{C}^{\mathrm{2}} +{S}^{\mathrm{2}} }={e}^{{zcos}\theta} \\ $$$${ln}\left(\sqrt{{C}^{\mathrm{2}} +{S}^{\mathrm{2}} }\right)={zcos}\theta\Leftrightarrow{zcos}\theta=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({C}^{\mathrm{2}} +{S}^{\mathrm{2}} \right) \\ $$$${and} \\ $$$${e}^{{itan}^{−\mathrm{1}} \left({S}/{C}\right)} ={e}^{{izsin}\theta} \Leftrightarrow{tan}^{−\mathrm{1}} \left({S}/{C}\right)={zsin}\theta \\ $$
Commented by Smail last updated on 04/Sep/19
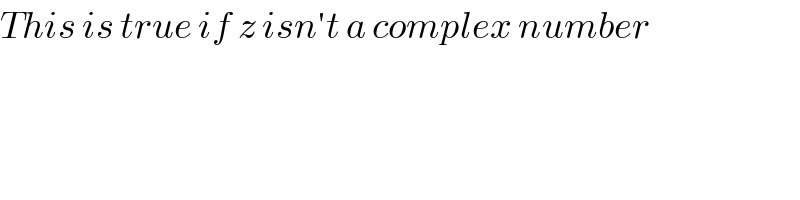
$${This}\:{is}\:{true}\:{if}\:{z}\:{isn}'{t}\:{a}\:{complex}\:{number} \\ $$
Commented by mathmax by abdo last updated on 04/Sep/19
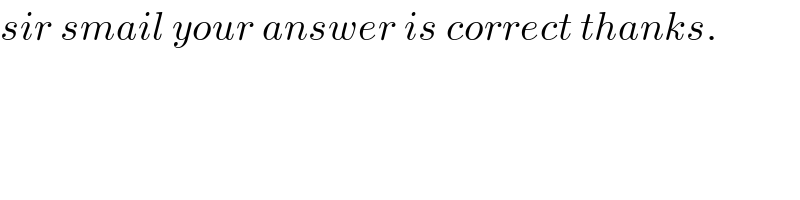
$${sir}\:{smail}\:{your}\:{answer}\:{is}\:{correct}\:{thanks}. \\ $$
