Question Number 68183 by ajfour last updated on 06/Sep/19
Commented by ajfour last updated on 06/Sep/19

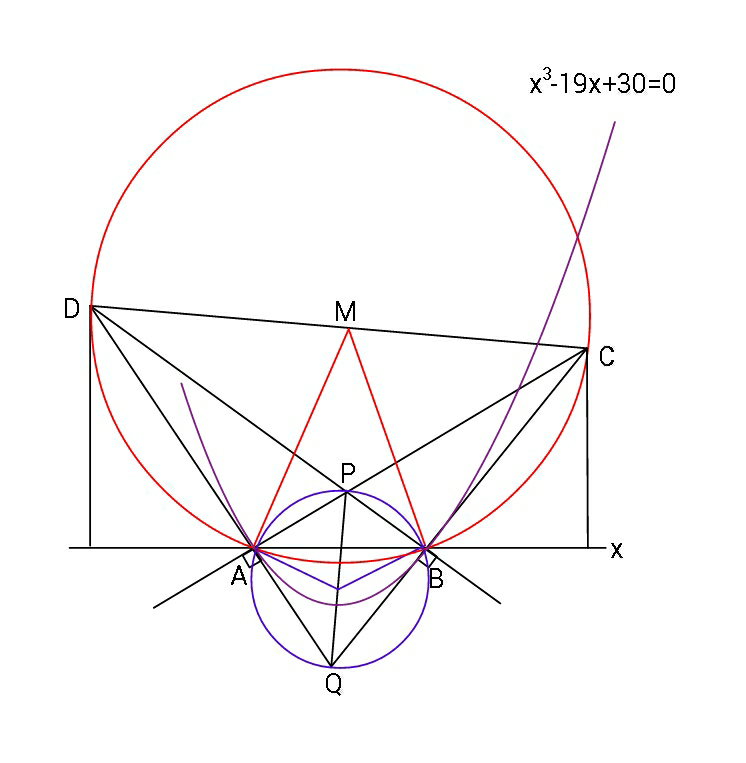
$${QBC}\:{and}\:{BPD}\:{are}\:{tangent}\:{and} \\ $$$${normal}\:{respectively}\:{to} \\ $$$${the}\:{cubic}\:{function}\:{y}={x}^{\mathrm{3}} −\mathrm{19}{x}+\mathrm{30} \\ $$$${at}\:{one}\:{of}\:{its}\:{root}\:{and}\:{QAD}\:{and} \\ $$$${AP}\:{C}\:\:{are}\:{again}\:{tangent}\:{and} \\ $$$${normal}\:{respectively}\:{to}\:{the} \\ $$$${same}\:{function}\:{at}\:{one}\:{of}\:{its}\:{other} \\ $$$${root}.\:{Circumcircles}\:{are}\:{drawn} \\ $$$${to}\:{quadrilaterals}\:{ABCD}\:{and} \\ $$$${APBQ}.\:\:{Find}\:{their}\:{radii}\:{and} \\ $$$${prove}\:{that}\:{PQ}\:{is}\:\bot\:{to}\:{CD}. \\ $$
