Menu Close

Question-68342

Tinku Tara 0 Comments
Pin




Question Number 68342 by Tony Lin last updated on 09/Sep/19
Commented by Tony Lin last updated on 09/Sep/19
when m slide to the bottom if there is no fraction find v_m &v_M find a_m &a_M
$${when}\:{m}\:{slide}\:{to}\:{the}\:{bottom} \\ $$$${if}\:{there}\:{is}\:{no}\:{fraction} \\ $$$${find}\:{v}_{{m}} \&{v}_{{M}} \\ $$$${find}\:{a}_{{m}} \&{a}_{{M}} \\ $$
Answered by mr W last updated on 09/Sep/19
Commented by mr W last updated on 10/Sep/19
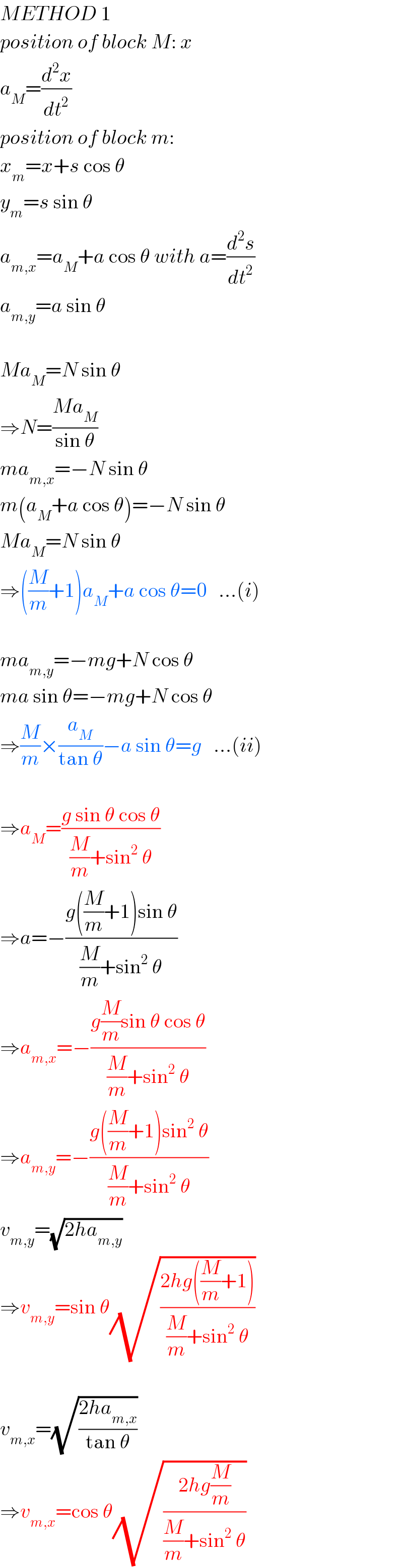
METHOD 1 position of block M: x a_M =(d^2 x/dt^2 ) position of block m: x_m =x+s cos θ y_m =s sin θ a_(m,x) =a_M +a cos θ with a=(d^2 s/dt^2 ) a_(m,y) =a sin θ Ma_M =N sin θ ⇒N=((Ma_M )/(sin θ)) ma_(m,x) =−N sin θ m(a_M +a cos θ)=−N sin θ Ma_M =N sin θ ⇒((M/m)+1)a_M +a cos θ=0 ...(i) ma_(m,y) =−mg+N cos θ ma sin θ=−mg+N cos θ ⇒(M/m)×(a_M /(tan θ))−a sin θ=g ...(ii) ⇒a_M =((g sin θ cos θ)/((M/m)+sin^2 θ)) ⇒a=−((g((M/m)+1)sin θ)/((M/m)+sin^2 θ)) ⇒a_(m,x) =−((g(M/m)sin θ cos θ)/((M/m)+sin^2 θ)) ⇒a_(m,y) =−((g((M/m)+1)sin^2 θ)/((M/m)+sin^2 θ)) v_(m,y) =(√(2ha_(m,y) )) ⇒v_(m,y) =sin θ(√((2hg((M/m)+1))/((M/m)+sin^2 θ))) v_(m,x) =(√((2ha_(m,x) )/(tan θ))) ⇒v_(m,x) =cos θ(√((2hg(M/m))/((M/m)+sin^2 θ)))
$${METHOD}\:\mathrm{1} \\ $$$${position}\:{of}\:{block}\:{M}:\:{x} \\ $$$${a}_{{M}} =\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} } \\ $$$${position}\:{of}\:{block}\:{m}: \\ $$$${x}_{{m}} ={x}+{s}\:\mathrm{cos}\:\theta \\ $$$${y}_{{m}} ={s}\:\mathrm{sin}\:\theta \\ $$$${a}_{{m},{x}} ={a}_{{M}} +{a}\:\mathrm{cos}\:\theta\:{with}\:{a}=\frac{{d}^{\mathrm{2}} {s}}{{dt}^{\mathrm{2}} } \\ $$$${a}_{{m},{y}} ={a}\:\mathrm{sin}\:\theta \\ $$$$ \\ $$$${Ma}_{{M}} ={N}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{N}=\frac{{Ma}_{{M}} }{\mathrm{sin}\:\theta} \\ $$$${ma}_{{m},{x}} =−{N}\:\mathrm{sin}\:\theta \\ $$$${m}\left({a}_{{M}} +{a}\:\mathrm{cos}\:\theta\right)=−{N}\:\mathrm{sin}\:\theta \\ $$$${Ma}_{{M}} ={N}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\left(\frac{{M}}{{m}}+\mathrm{1}\right){a}_{{M}} +{a}\:\mathrm{cos}\:\theta=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${ma}_{{m},{y}} =−{mg}+{N}\:\mathrm{cos}\:\theta \\ $$$${ma}\:\mathrm{sin}\:\theta=−{mg}+{N}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\frac{{M}}{{m}}×\frac{{a}_{{M}} }{\mathrm{tan}\:\theta}−{a}\:\mathrm{sin}\:\theta={g}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\Rightarrow{a}_{{M}} =\frac{{g}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{a}=−\frac{{g}\left(\frac{{M}}{{m}}+\mathrm{1}\right)\mathrm{sin}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{a}_{{m},{x}} =−\frac{{g}\frac{{M}}{{m}}\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{a}_{{m},{y}} =−\frac{{g}\left(\frac{{M}}{{m}}+\mathrm{1}\right)\mathrm{sin}^{\mathrm{2}} \:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$${v}_{{m},{y}} =\sqrt{\mathrm{2}{ha}_{{m},{y}} } \\ $$$$\Rightarrow{v}_{{m},{y}} =\mathrm{sin}\:\theta\sqrt{\frac{\mathrm{2}{hg}\left(\frac{{M}}{{m}}+\mathrm{1}\right)}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$ \\ $$$${v}_{{m},{x}} =\sqrt{\frac{\mathrm{2}{ha}_{{m},{x}} }{\mathrm{tan}\:\theta}} \\ $$$$\Rightarrow{v}_{{m},{x}} =\mathrm{cos}\:\theta\sqrt{\frac{\mathrm{2}{hg}\frac{{M}}{{m}}}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$
Commented by Tony Lin last updated on 10/Sep/19
thanks sir
$${thanks}\:{sir} \\ $$
Answered by mr W last updated on 09/Sep/19
Commented by mr W last updated on 09/Sep/19
METHOD 2 Ma_M =N sin θ ⇒N=((Ma_M )/(sin θ)) N+ma_M sin θ=mg cos θ ((Ma_M )/(sin θ))+ma_M sin θ=mg cos θ ((M/m)+sin^2 θ)a_M =g sin θcos θ ⇒a_M =((g sin θ cos θ)/((M/m)+sin^2 θ)) ma_M cos θ+mg sin θ=ma a=a_M cos θ+g sin θ ⇒a=((g((M/m)+1)sin θ)/((M/m)+sin^2 θ)) a_(m,x) =a cos θ−a_M =((g((M/m)+1)sin θ cos θ)/((M/m)+sin^2 θ))−((g sin θ cos θ)/((M/m)+sin^2 θ)) ⇒a_(m,x) =(((M/m)g sin θ cos θ)/((M/m)+sin^2 θ)) a_(m,y) =a sin θ ⇒a_(m,y) =((g((M/m)+1)sin^2 θ)/((M/m)+sin^2 θ))
$${METHOD}\:\mathrm{2} \\ $$$${Ma}_{{M}} ={N}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{N}=\frac{{Ma}_{{M}} }{\mathrm{sin}\:\theta} \\ $$$$ \\ $$$${N}+{ma}_{{M}} \mathrm{sin}\:\theta={mg}\:\mathrm{cos}\:\theta \\ $$$$\frac{{Ma}_{{M}} }{\mathrm{sin}\:\theta}+{ma}_{{M}} \mathrm{sin}\:\theta={mg}\:\mathrm{cos}\:\theta \\ $$$$\left(\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta\right){a}_{{M}} ={g}\:\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\Rightarrow{a}_{{M}} =\frac{{g}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$ \\ $$$${ma}_{{M}} \mathrm{cos}\:\theta+{mg}\:\mathrm{sin}\:\theta={ma} \\ $$$${a}={a}_{{M}} \mathrm{cos}\:\theta+{g}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{a}=\frac{{g}\left(\frac{{M}}{{m}}+\mathrm{1}\right)\mathrm{sin}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$${a}_{{m},{x}} ={a}\:\mathrm{cos}\:\theta−{a}_{{M}} =\frac{{g}\left(\frac{{M}}{{m}}+\mathrm{1}\right)\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta}−\frac{{g}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{a}_{{m},{x}} =\frac{\frac{{M}}{{m}}{g}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$${a}_{{m},{y}} ={a}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{a}_{{m},{y}} =\frac{{g}\left(\frac{{M}}{{m}}+\mathrm{1}\right)\mathrm{sin}^{\mathrm{2}} \:\theta}{\frac{{M}}{{m}}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$
Commented by Tony Lin last updated on 10/Sep/19
thanks sir
$${thanks}\:{sir} \\ $$
Answered by Tanmay chaudhury last updated on 09/Sep/19
Commented by Tanmay chaudhury last updated on 09/Sep/19
Mg+Ncosθ=N_G MA=Nsinθ for m mgsinθ+mAcosθ=ma mgcosθ=N+mAsinθ MA=sinθ(mgcosθ−mAsinθ) A(M+msin^2 θ)=mgsinθcosθ A=((mgsinθcosθ)/(M+msin^2 θ)) A=acc of wedge a=gsinθ+(((mgsinθcosθ)/(M+msin^2 θ)))cosθ a=((Mgsinθ+mgsin^3 θ+mgsinθcos^2 θ)/(M+msin^2 θ)) a=((Mgsinθ+mgsinθ(sin^2 θ+cos^2 θ))/(M+msin^2 θ)) a=(((M+m)gsinθ)/(M+msin^2 θ))
$${Mg}+{Ncos}\theta={N}_{{G}} \\ $$$${MA}={Nsin}\theta \\ $$$${for}\:{m} \\ $$$${mgsin}\theta+{mAcos}\theta={ma} \\ $$$${mgcos}\theta={N}+{mAsin}\theta \\ $$$${MA}={sin}\theta\left({mgcos}\theta−{mAsin}\theta\right) \\ $$$${A}\left({M}+{msin}^{\mathrm{2}} \theta\right)={mgsin}\theta{cos}\theta \\ $$$${A}=\frac{{mgsin}\theta{cos}\theta}{{M}+{msin}^{\mathrm{2}} \theta} \\ $$$${A}={acc}\:{of}\:{wedge} \\ $$$${a}={gsin}\theta+\left(\frac{{mgsin}\theta{cos}\theta}{{M}+{msin}^{\mathrm{2}} \theta}\right){cos}\theta \\ $$$${a}=\frac{{Mgsin}\theta+{mgsin}^{\mathrm{3}} \theta+{mgsin}\theta{cos}^{\mathrm{2}} \theta}{{M}+{msin}^{\mathrm{2}} \theta} \\ $$$${a}=\frac{{Mgsin}\theta+{mgsin}\theta\left({sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta\right)}{{M}+{msin}^{\mathrm{2}} \theta} \\ $$$${a}=\frac{\left({M}+{m}\right){gsin}\theta}{{M}+{msin}^{\mathrm{2}} \theta} \\ $$$$ \\ $$$$ \\ $$
Commented by Tony Lin last updated on 10/Sep/19
thanks sir
$${thanks}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *