Menu Close

Question-68350

Tinku Tara 0 Comments
Pin




Question Number 68350 by mhmd last updated on 09/Sep/19
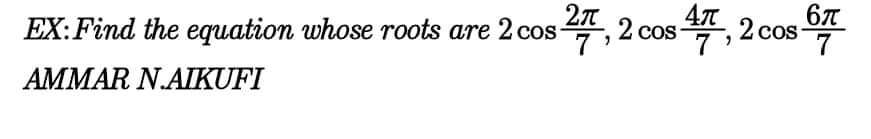
Commented by MJS last updated on 09/Sep/19
(x−2cos ((2π)/7))(x−2cos ((4π)/7))(x−cos ((6π)/7))=0 approximating leads to x^3 +x^2 −2x−1=0 we have to show that −2(cos ((2π)/7)+cos ((4π)/7) +cos ((6π)/7))=1 4(cos ((2π)/7) cos ((4π)/7) +cos ((2π)/7) cos ((6π)/7) +cos ((4π)/7) cos ((6π)/7))=−2 −8cos ((2π)/7) cos ((4π)/7) cos ((6π)/7) =−1 or: x^3 +x^2 −2x−1=0 the solutions (following trigonometric method) are x_1 =−(1/3)+((2(√7))/3)sin ((π/3)+(1/3)arcsin ((√7)/(14))) x_2 =−(1/3)−((2(√7))/3)cos ((π/6)+(1/3)arcsin ((√7)/(14))) x_3 =−(1/3)−((2(√7))/3)sin ((1/3)arcsin ((√7)/(14))) we have to show that x_1 =2cos ((2π)/7); x_2 =2cos ((6π)/7); x_3 =2cos ((4π)/7)
$$\left({x}−\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\left({x}−\mathrm{2cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\right)\left({x}−\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{7}}\right)=\mathrm{0} \\ $$$$\mathrm{approximating}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that} \\ $$$$−\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:+\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{7}}\right)=\mathrm{1} \\ $$$$\mathrm{4}\left(\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{7}}\:+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{7}}\right)=−\mathrm{2} \\ $$$$−\mathrm{8cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{7}}\:=−\mathrm{1} \\ $$$$\mathrm{or}: \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{solutions}\:\left(\mathrm{following}\:\mathrm{trigonometric}\:\mathrm{method}\right) \\ $$$$\mathrm{are} \\ $$$${x}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right) \\ $$$${x}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right) \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that} \\ $$$${x}_{\mathrm{1}} =\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}};\:{x}_{\mathrm{2}} =\mathrm{2cos}\:\frac{\mathrm{6}\pi}{\mathrm{7}};\:{x}_{\mathrm{3}} =\mathrm{2cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}} \\ $$
Commented by peter frank last updated on 09/Sep/19
thank you
$${thank}\:{you} \\ $$
Answered by mind is power last updated on 09/Sep/19
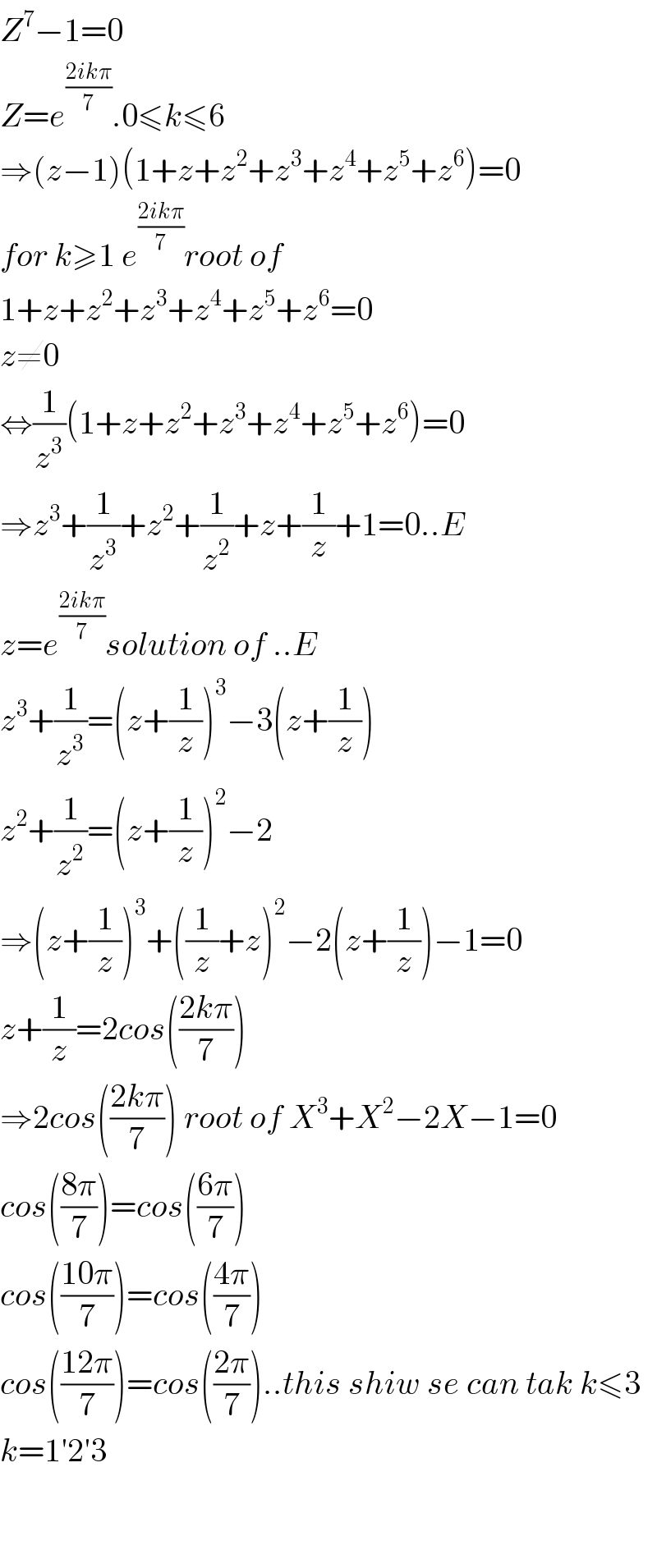
Z^7 −1=0 Z=e^((2ikπ)/7) .0≤k≤6 ⇒(z−1)(1+z+z^2 +z^3 +z^4 +z^5 +z^6 )=0 for k≥1 e^((2ikπ)/7) root of 1+z+z^2 +z^3 +z^4 +z^5 +z^6 =0 z≠0 ⇔(1/z^3 )(1+z+z^2 +z^3 +z^4 +z^5 +z^6 )=0 ⇒z^3 +(1/z^3 )+z^2 +(1/z^2 )+z+(1/z)+1=0..E z=e^((2ikπ)/7) solution of ..E z^3 +(1/z^3 )=(z+(1/z))^3 −3(z+(1/z)) z^2 +(1/z^2 )=(z+(1/z))^2 −2 ⇒(z+(1/z))^3 +((1/z)+z)^2 −2(z+(1/z))−1=0 z+(1/z)=2cos(((2kπ)/7)) ⇒2cos(((2kπ)/7)) root of X^3 +X^2 −2X−1=0 cos(((8π)/7))=cos(((6π)/7)) cos(((10π)/7))=cos(((4π)/7)) cos(((12π)/7))=cos(((2π)/7))..this shiw se can tak k≤3 k=1′2′3
$${Z}^{\mathrm{7}} −\mathrm{1}=\mathrm{0} \\ $$$${Z}={e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{7}}} .\mathrm{0}\leqslant{k}\leqslant\mathrm{6} \\ $$$$\Rightarrow\left({z}−\mathrm{1}\right)\left(\mathrm{1}+{z}+{z}^{\mathrm{2}} +{z}^{\mathrm{3}} +{z}^{\mathrm{4}} +{z}^{\mathrm{5}} +{z}^{\mathrm{6}} \right)=\mathrm{0} \\ $$$${for}\:{k}\geqslant\mathrm{1}\:{e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{7}}} {root}\:{of}\: \\ $$$$\mathrm{1}+{z}+{z}^{\mathrm{2}} +{z}^{\mathrm{3}} +{z}^{\mathrm{4}} +{z}^{\mathrm{5}} +{z}^{\mathrm{6}} =\mathrm{0} \\ $$$${z}\neq\mathrm{0} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{{z}^{\mathrm{3}} }\left(\mathrm{1}+{z}+{z}^{\mathrm{2}} +{z}^{\mathrm{3}} +{z}^{\mathrm{4}} +{z}^{\mathrm{5}} +{z}^{\mathrm{6}} \right)=\mathrm{0} \\ $$$$\Rightarrow{z}^{\mathrm{3}} +\frac{\mathrm{1}}{{z}^{\mathrm{3}} }+{z}^{\mathrm{2}} +\frac{\mathrm{1}}{{z}^{\mathrm{2}} }+{z}+\frac{\mathrm{1}}{{z}}+\mathrm{1}=\mathrm{0}..{E} \\ $$$${z}={e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{7}}} {solution}\:{of}\:..{E} \\ $$$${z}^{\mathrm{3}} +\frac{\mathrm{1}}{{z}^{\mathrm{3}} }=\left({z}+\frac{\mathrm{1}}{{z}}\right)^{\mathrm{3}} −\mathrm{3}\left({z}+\frac{\mathrm{1}}{{z}}\right) \\ $$$${z}^{\mathrm{2}} +\frac{\mathrm{1}}{{z}^{\mathrm{2}} }=\left({z}+\frac{\mathrm{1}}{{z}}\right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\Rightarrow\left({z}+\frac{\mathrm{1}}{{z}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{1}}{{z}}+{z}\right)^{\mathrm{2}} −\mathrm{2}\left({z}+\frac{\mathrm{1}}{{z}}\right)−\mathrm{1}=\mathrm{0} \\ $$$${z}+\frac{\mathrm{1}}{{z}}=\mathrm{2}{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right) \\ $$$$\Rightarrow\mathrm{2}{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{7}}\right)\:{root}\:{of}\:{X}^{\mathrm{3}} +{X}^{\mathrm{2}} −\mathrm{2}{X}−\mathrm{1}=\mathrm{0} \\ $$$${cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)={cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right) \\ $$$${cos}\left(\frac{\mathrm{10}\pi}{\mathrm{7}}\right)={cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right) \\ $$$${cos}\left(\frac{\mathrm{12}\pi}{\mathrm{7}}\right)={cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)..{this}\:{shiw}\:{se}\:{can}\:{tak}\:{k}\leqslant\mathrm{3} \\ $$$${k}=\mathrm{1}'\mathrm{2}'\mathrm{3} \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 09/Sep/19
great, thank you!
$$\mathrm{great},\:\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by mind is power last updated on 09/Sep/19
y′re welcom
$${y}'{re}\:{welcom} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *