Question Number 68576 by naka3546 last updated on 13/Sep/19
Commented by naka3546 last updated on 13/Sep/19
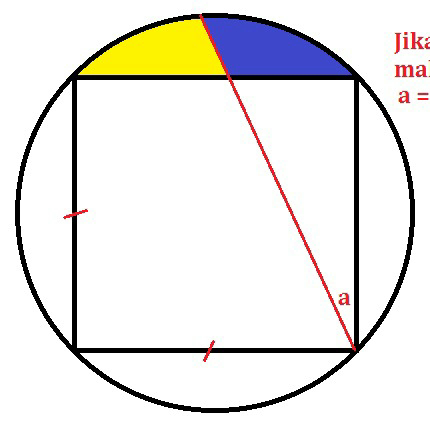
![Find a , if [ yellow ] = [ blue ] Area of yellow = area of blue](https://www.tinkutara.com/question/Q68577.png)
$${Find}\:\:{a}\:\:,\:\:{if}\:\:\left[\:{yellow}\:\right]\:=\:\:\left[\:{blue}\:\right] \\ $$$${Area}\:\:{of}\:\:{yellow}\:\:=\:\:{area}\:\:{of}\:\:{blue} \\ $$
Answered by mr W last updated on 14/Sep/19
![let R=1 (1^2 /2)[(π/2)+2a−sin ((π/2)+2a)]−(1^2 /2)((π/2)−sin (π/2))−((√2)/2)×(√2) tan a=(1/2)×(1^2 /2)((π/2)−sin (π/2)) ⇒2a−cos 2a−2 tan a=(π/4)−(3/2) ⇒cos^2 a+tan a−a=((10−π)/8) ⇒a≈0.4255=24.38°](https://www.tinkutara.com/question/Q68581.png)
$${let}\:{R}=\mathrm{1} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\pi}{\mathrm{2}}+\mathrm{2}{a}−\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{a}\right)\right]−\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\right)−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\sqrt{\mathrm{2}}\:\mathrm{tan}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{2}{a}−\mathrm{cos}\:\mathrm{2}{a}−\mathrm{2}\:\mathrm{tan}\:{a}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} {a}+\mathrm{tan}\:{a}−{a}=\frac{\mathrm{10}−\pi}{\mathrm{8}} \\ $$$$\Rightarrow{a}\approx\mathrm{0}.\mathrm{4255}=\mathrm{24}.\mathrm{38}° \\ $$
