Question Number 68589 by peter frank last updated on 13/Sep/19
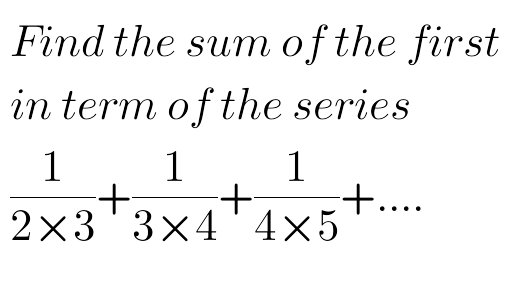
Answered by $@ty@m123 last updated on 14/Sep/19
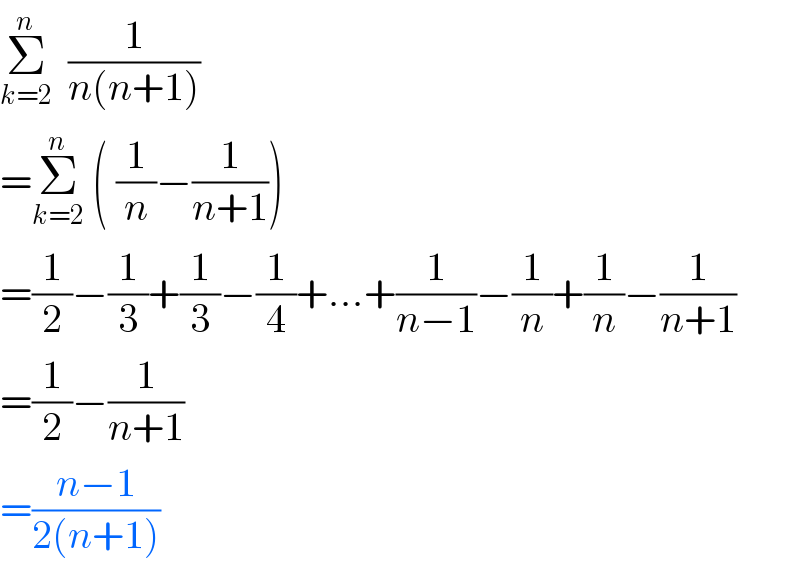
$$\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$$=\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\:\left(\:\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$=\frac{{n}−\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)} \\ $$
Commented by peter frank last updated on 14/Sep/19

$${thank}\:{you} \\ $$
