Question-68912

Question Number 68912 by TawaTawa last updated on 16/Sep/19

Answered by MJS last updated on 17/Sep/19

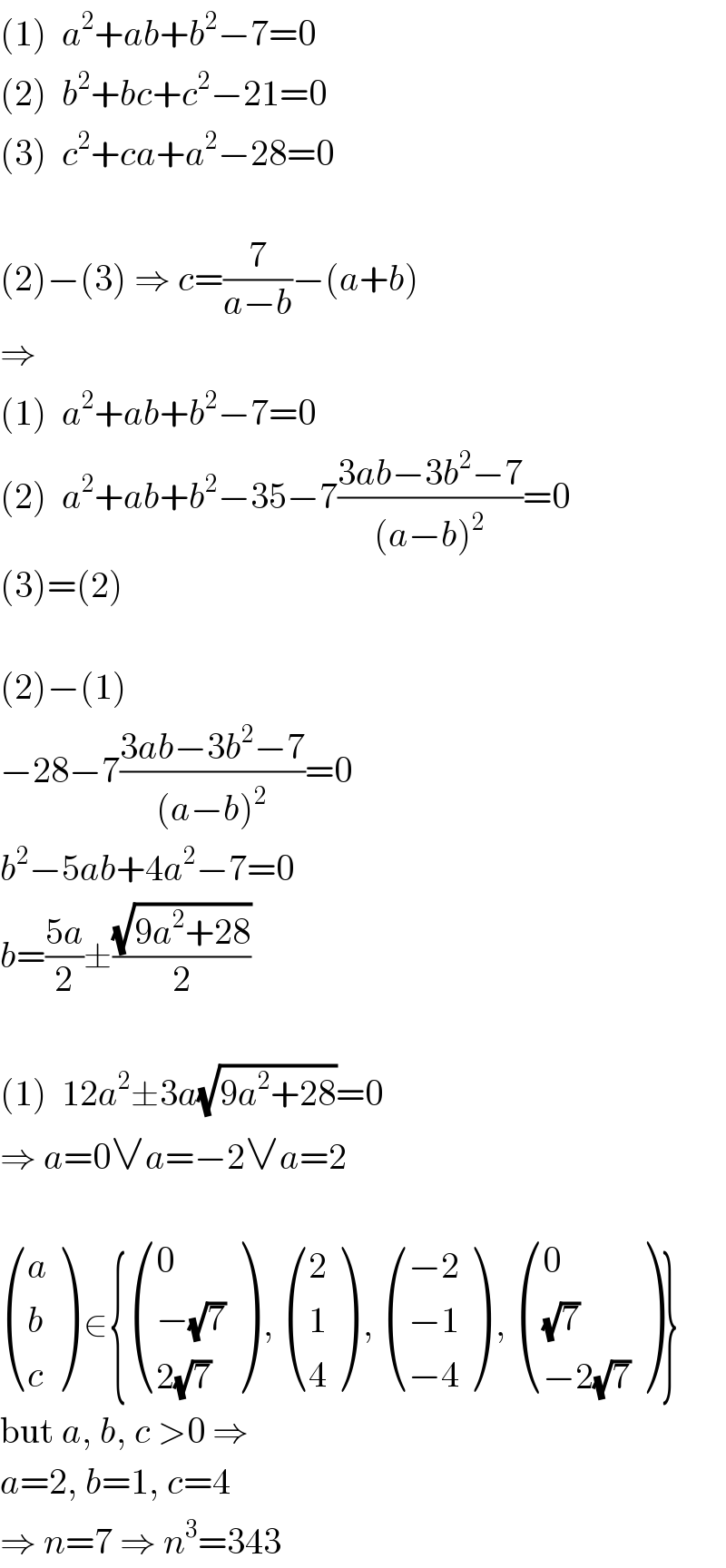
(1) a^2 +ab+b^2 −7=0 (2) b^2 +bc+c^2 −21=0 (3) c^2 +ca+a^2 −28=0 (2)−(3) ⇒ c=(7/(a−b))−(a+b) ⇒ (1) a^2 +ab+b^2 −7=0 (2) a^2 +ab+b^2 −35−7((3ab−3b^2 −7)/((a−b)^2 ))=0 (3)=(2) (2)−(1) −28−7((3ab−3b^2 −7)/((a−b)^2 ))=0 b^2 −5ab+4a^2 −7=0 b=((5a)/2)±((√(9a^2 +28))/2) (1) 12a^2 ±3a(√(9a^2 +28))=0 ⇒ a=0∨a=−2∨a=2 ((a),(b),(c) ) ∈{ ((0),((−(√7))),((2(√7))) ) , ((2),(1),(4) ) , (((−2)),((−1)),((−4)) ) , ((0),((√7)),((−2(√7))) )} but a, b, c >0 ⇒ a=2, b=1, c=4 ⇒ n=7 ⇒ n^3 =343

$$\left(\mathrm{1}\right)\:\:{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} −\mathrm{7}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} −\mathrm{21}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:{c}^{\mathrm{2}} +{ca}+{a}^{\mathrm{2}} −\mathrm{28}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{3}\right)\:\Rightarrow\:{c}=\frac{\mathrm{7}}{{a}−{b}}−\left({a}+{b}\right) \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{1}\right)\:\:{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} −\mathrm{7}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} −\mathrm{35}−\mathrm{7}\frac{\mathrm{3}{ab}−\mathrm{3}{b}^{\mathrm{2}} −\mathrm{7}}{\left({a}−{b}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)=\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right) \\ $$$$−\mathrm{28}−\mathrm{7}\frac{\mathrm{3}{ab}−\mathrm{3}{b}^{\mathrm{2}} −\mathrm{7}}{\left({a}−{b}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$${b}^{\mathrm{2}} −\mathrm{5}{ab}+\mathrm{4}{a}^{\mathrm{2}} −\mathrm{7}=\mathrm{0} \\ $$$${b}=\frac{\mathrm{5}{a}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{9}{a}^{\mathrm{2}} +\mathrm{28}}}{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{12}{a}^{\mathrm{2}} \pm\mathrm{3}{a}\sqrt{\mathrm{9}{a}^{\mathrm{2}} +\mathrm{28}}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=\mathrm{0}\vee{a}=−\mathrm{2}\vee{a}=\mathrm{2} \\ $$$$ \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\\{{c}}\end{pmatrix}\:\in\left\{\begin{pmatrix}{\mathrm{0}}\\{−\sqrt{\mathrm{7}}}\\{\mathrm{2}\sqrt{\mathrm{7}}}\end{pmatrix}\:,\:\begin{pmatrix}{\mathrm{2}}\\{\mathrm{1}}\\{\mathrm{4}}\end{pmatrix}\:,\:\begin{pmatrix}{−\mathrm{2}}\\{−\mathrm{1}}\\{−\mathrm{4}}\end{pmatrix}\:,\:\begin{pmatrix}{\mathrm{0}}\\{\sqrt{\mathrm{7}}}\\{−\mathrm{2}\sqrt{\mathrm{7}}}\end{pmatrix}\right\} \\ $$$$\mathrm{but}\:{a},\:{b},\:{c}\:>\mathrm{0}\:\Rightarrow \\ $$$${a}=\mathrm{2},\:{b}=\mathrm{1},\:{c}=\mathrm{4} \\ $$$$\Rightarrow\:{n}=\mathrm{7}\:\Rightarrow\:{n}^{\mathrm{3}} =\mathrm{343} \\ $$

Commented by TawaTawa last updated on 17/Sep/19

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply