Question Number 69098 by rajesh4661kumar@gmail.com last updated on 20/Sep/19
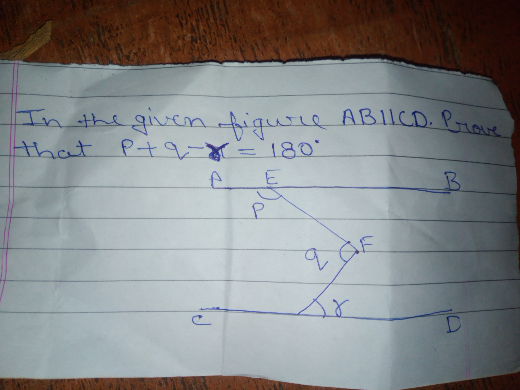
Commented by Kunal12588 last updated on 20/Sep/19

$${its}\:{really}\:{easy}\:{just}\:{construct}\:{a}\:{line}\:{through} \\ $$$${F}\:{parallel}\:{to}\:{AB}\:\&\:{CD}.\:{and}\:{remember}\:{the} \\ $$$${property}\:{of}\:{alternate}\:{interior}\:{angles}\:{and} \\ $$$${consectutive}\:{interior}\:{angles} \\ $$
Commented by $@ty@m123 last updated on 20/Sep/19

Commented by Henri Boucatchou last updated on 20/Sep/19

Answered by $@ty@m123 last updated on 20/Sep/19

$${Draw}\:{a}\:{st}.\:{line}\:{through}\:{F} \\ $$$${parallel}\:{to}\:{AB}\:{and}\:{CD}. \\ $$$${Let}\:{q}={x}+{y}\:{as}\:{shown}\:{in}\:{figure}. \\ $$$${We}\:{have}, \\ $$$${p}+{x}=\mathrm{180}^{\mathrm{o}} \:−−\left(\mathrm{1}\right) \\ $$$${y}={r}\:−−−−\left(\mathrm{2}\right) \\ $$$${Add}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$${p}+{x}+{y}=\mathrm{180}^{\mathrm{o}} +\mathrm{r} \\ $$$$\Rightarrow\:{p}+{q}−{r}=\mathrm{180}^{\mathrm{o}} \\ $$
