Question Number 69123 by TawaTawa last updated on 20/Sep/19
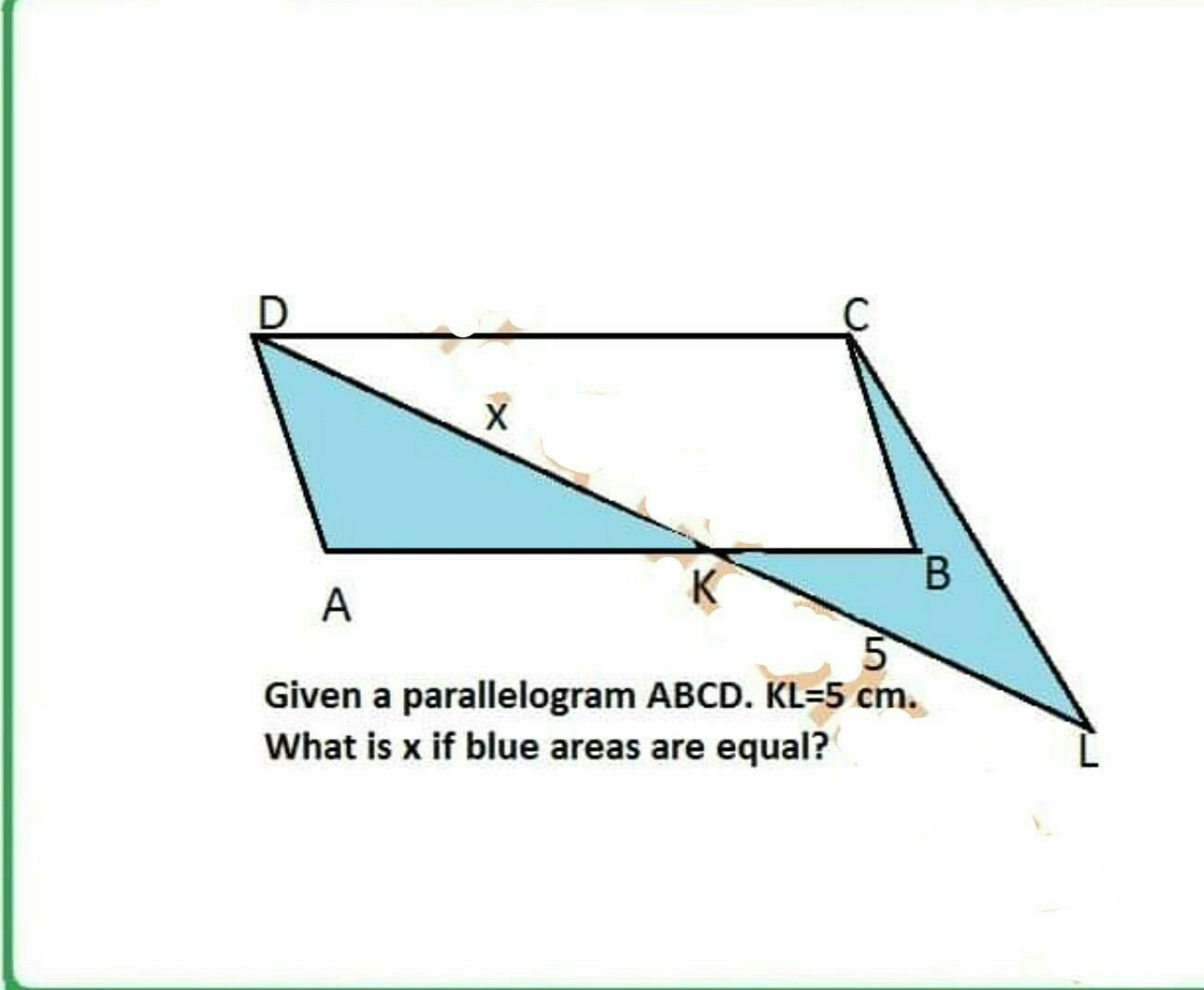
Answered by mr W last updated on 20/Sep/19
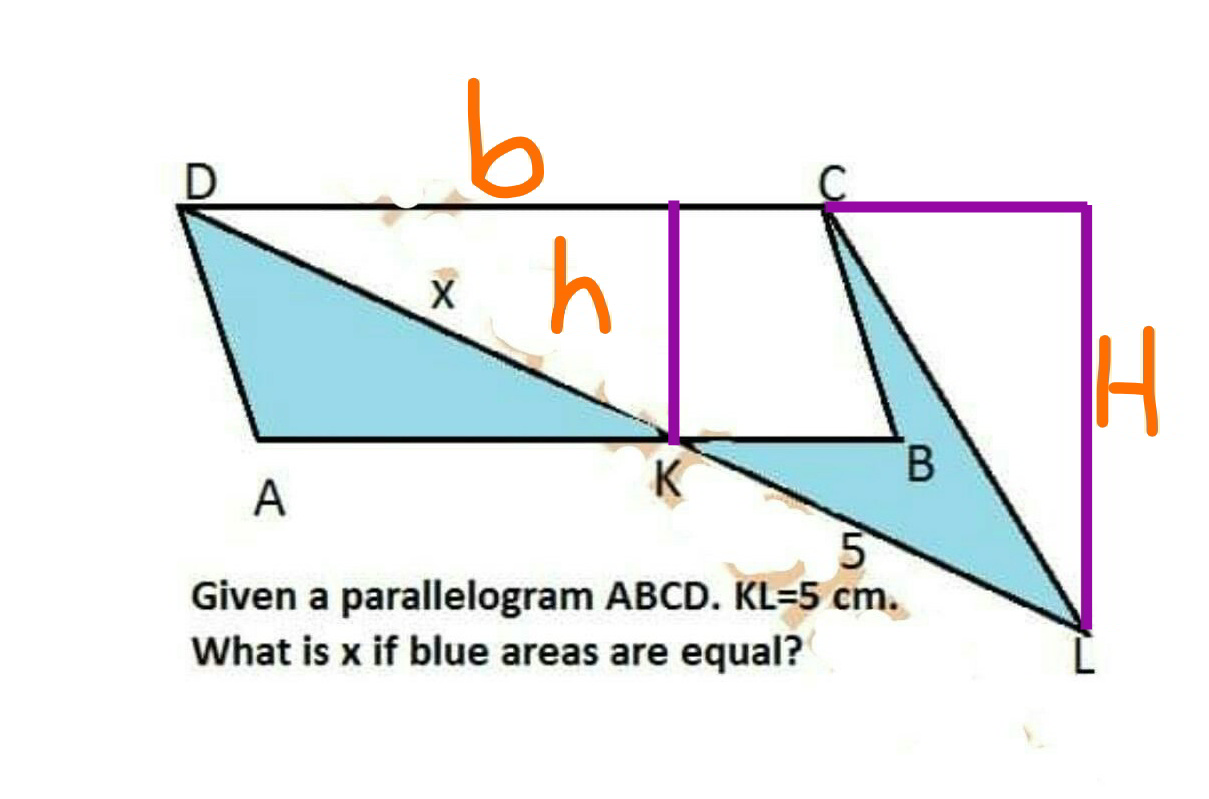
Commented by mr W last updated on 20/Sep/19
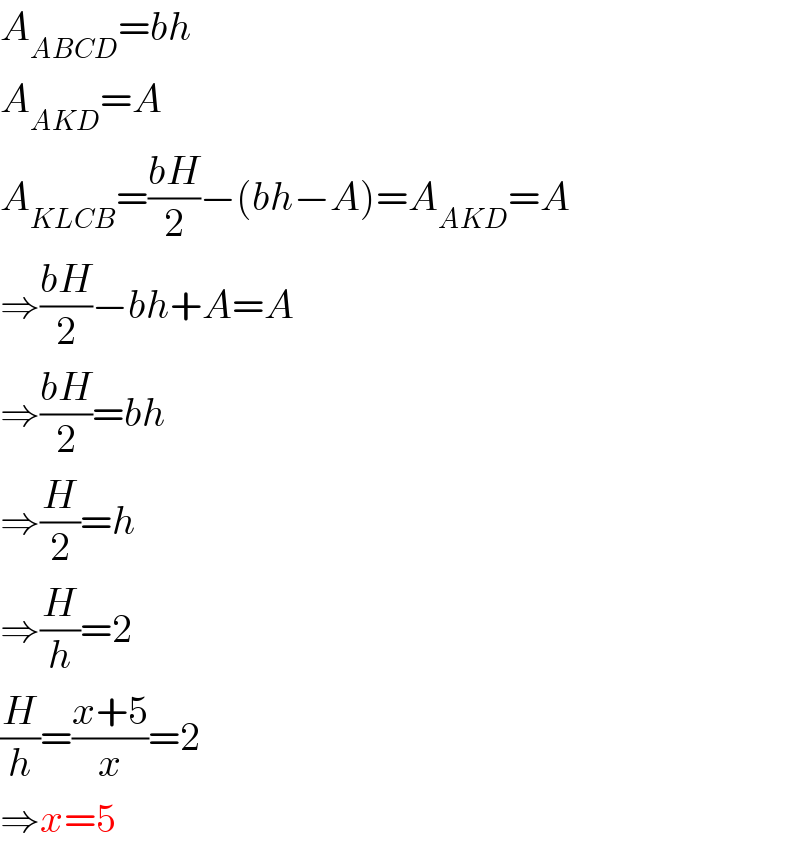
$${A}_{{ABCD}} ={bh} \\ $$$${A}_{{AKD}} ={A} \\ $$$${A}_{{KLCB}} =\frac{{bH}}{\mathrm{2}}−\left({bh}−{A}\right)={A}_{{AKD}} ={A} \\ $$$$\Rightarrow\frac{{bH}}{\mathrm{2}}−{bh}+{A}={A} \\ $$$$\Rightarrow\frac{{bH}}{\mathrm{2}}={bh} \\ $$$$\Rightarrow\frac{{H}}{\mathrm{2}}={h} \\ $$$$\Rightarrow\frac{{H}}{{h}}=\mathrm{2} \\ $$$$\frac{{H}}{{h}}=\frac{{x}+\mathrm{5}}{{x}}=\mathrm{2} \\ $$$$\Rightarrow{x}=\mathrm{5} \\ $$
Commented by TawaTawa last updated on 20/Sep/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
