Question Number 69268 by A8;15: last updated on 22/Sep/19
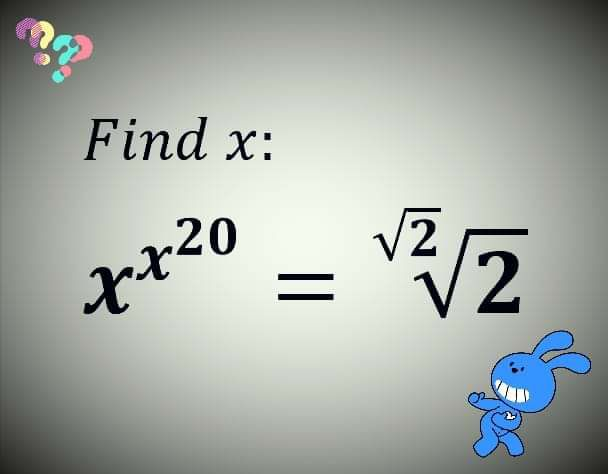
Answered by mr W last updated on 22/Sep/19
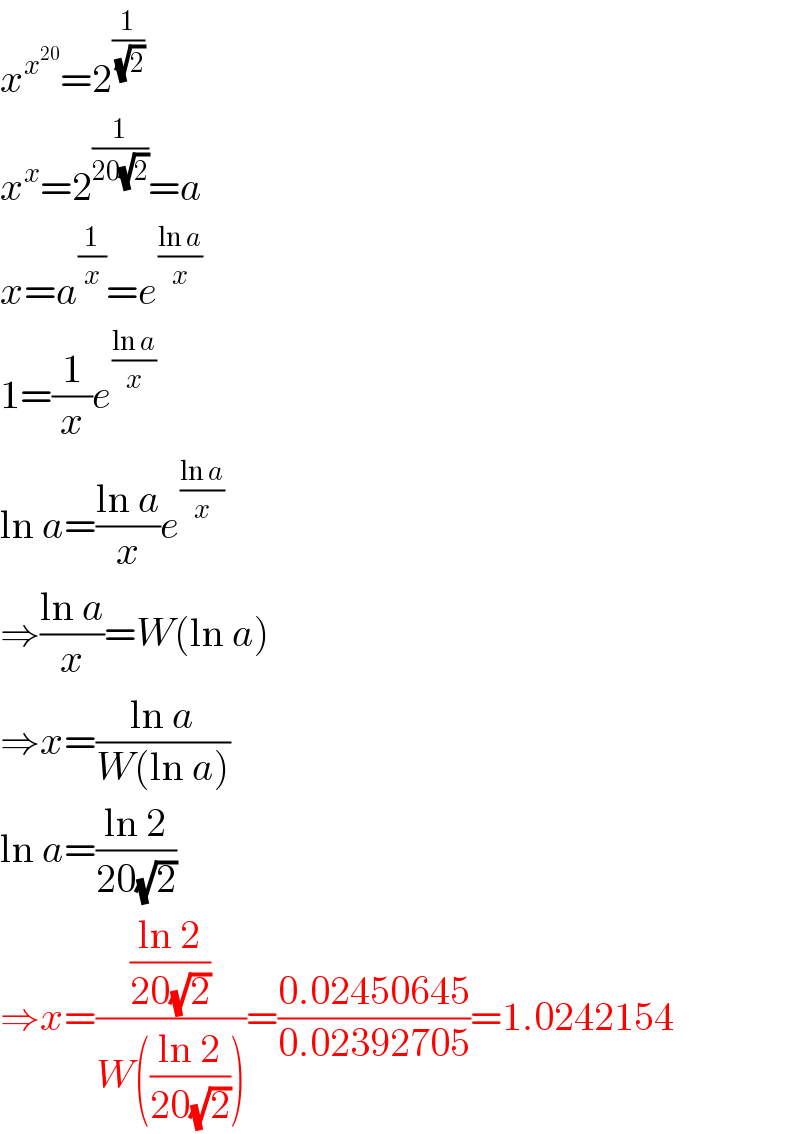
$${x}^{{x}^{\mathrm{20}} } =\mathrm{2}^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \\ $$$${x}^{{x}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{20}\sqrt{\mathrm{2}}}} ={a} \\ $$$${x}={a}^{\frac{\mathrm{1}}{{x}}} ={e}^{\frac{\mathrm{ln}\:{a}}{{x}}} \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{{x}}{e}^{\frac{\mathrm{ln}\:{a}}{{x}}} \\ $$$$\mathrm{ln}\:{a}=\frac{\mathrm{ln}\:{a}}{{x}}{e}^{\frac{\mathrm{ln}\:{a}}{{x}}} \\ $$$$\Rightarrow\frac{\mathrm{ln}\:{a}}{{x}}={W}\left(\mathrm{ln}\:{a}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:{a}}{{W}\left(\mathrm{ln}\:{a}\right)} \\ $$$$\mathrm{ln}\:{a}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{20}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{x}=\frac{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{20}\sqrt{\mathrm{2}}}}{{W}\left(\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{20}\sqrt{\mathrm{2}}}\right)}=\frac{\mathrm{0}.\mathrm{02450645}}{\mathrm{0}.\mathrm{02392705}}=\mathrm{1}.\mathrm{0242154} \\ $$
