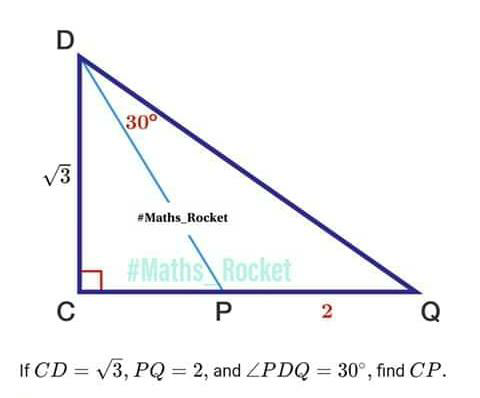
Question Number 69272 by TawaTawa last updated on 22/Sep/19
Answered by $@ty@m123 last updated on 22/Sep/19
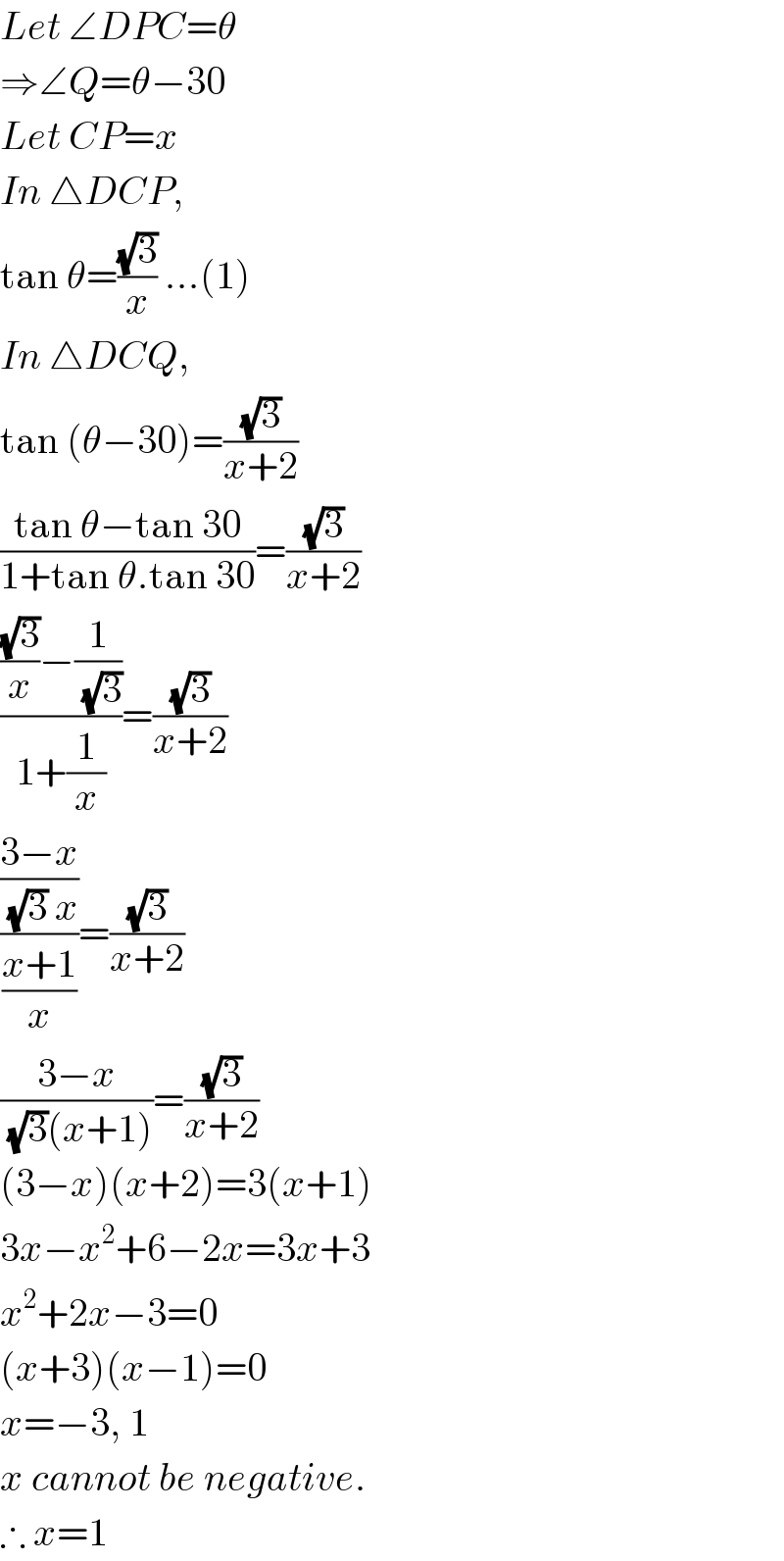
$${Let}\:\angle{DPC}=\theta \\ $$$$\Rightarrow\angle{Q}=\theta−\mathrm{30} \\ $$$${Let}\:{CP}={x} \\ $$$${In}\:\bigtriangleup{DCP}, \\ $$$$\mathrm{tan}\:\theta=\frac{\sqrt{\mathrm{3}}}{{x}}\:…\left(\mathrm{1}\right) \\ $$$${In}\:\bigtriangleup{DCQ}, \\ $$$$\mathrm{tan}\:\left(\theta−\mathrm{30}\right)=\frac{\sqrt{\mathrm{3}}}{{x}+\mathrm{2}} \\ $$$$\frac{\mathrm{tan}\:\theta−\mathrm{tan}\:\mathrm{30}}{\mathrm{1}+\mathrm{tan}\:\theta.\mathrm{tan}\:\mathrm{30}}=\frac{\sqrt{\mathrm{3}}}{{x}+\mathrm{2}} \\ $$$$\frac{\frac{\sqrt{\mathrm{3}}}{{x}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}}}=\frac{\sqrt{\mathrm{3}}}{{x}+\mathrm{2}} \\ $$$$\frac{\frac{\mathrm{3}−{x}}{\:\sqrt{\mathrm{3}}\:{x}}}{\frac{{x}+\mathrm{1}}{{x}}}=\frac{\sqrt{\mathrm{3}}}{{x}+\mathrm{2}} \\ $$$$\frac{\mathrm{3}−{x}}{\:\sqrt{\mathrm{3}}\left({x}+\mathrm{1}\right)}=\frac{\sqrt{\mathrm{3}}}{{x}+\mathrm{2}} \\ $$$$\left(\mathrm{3}−{x}\right)\left({x}+\mathrm{2}\right)=\mathrm{3}\left({x}+\mathrm{1}\right) \\ $$$$\mathrm{3}{x}−{x}^{\mathrm{2}} +\mathrm{6}−\mathrm{2}{x}=\mathrm{3}{x}+\mathrm{3} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\left({x}+\mathrm{3}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{3},\:\mathrm{1} \\ $$$${x}\:{cannot}\:{be}\:{negative}. \\ $$$$\therefore\:{x}=\mathrm{1} \\ $$
Commented by TawaTawa last updated on 22/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
