Question-69456

Question Number 69456 by TawaTawa last updated on 23/Sep/19

Commented by TawaTawa last updated on 23/Sep/19

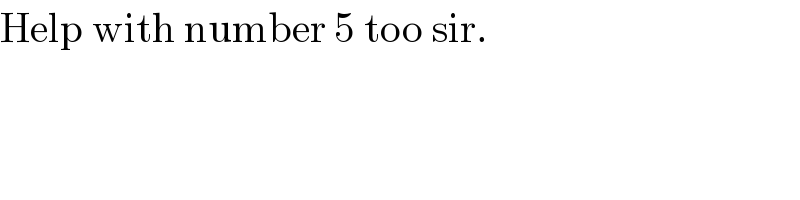
$$\mathrm{Help}\:\mathrm{with}\:\mathrm{number}\:\mathrm{5}\:\mathrm{too}\:\mathrm{sir}.\: \\ $$

Answered by mr W last updated on 23/Sep/19

r=radius of smallest circle 2^2 +(4−r)^2 =(2+r)^2 ⇒r=(4/3) A_(big semicircle) =((π×4^2 )/2)=8π A_(shaded) =8π−π×2^2 −π((4/3))^2 =((20π)/9) ratio=((20π)/(9×8π))=(5/(18))

$${r}={radius}\:{of}\:{smallest}\:{circle} \\ $$$$\mathrm{2}^{\mathrm{2}} +\left(\mathrm{4}−{r}\right)^{\mathrm{2}} =\left(\mathrm{2}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${A}_{{big}\:{semicircle}} =\frac{\pi×\mathrm{4}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{8}\pi \\ $$$${A}_{{shaded}} =\mathrm{8}\pi−\pi×\mathrm{2}^{\mathrm{2}} −\pi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\mathrm{20}\pi}{\mathrm{9}} \\ $$$${ratio}=\frac{\mathrm{20}\pi}{\mathrm{9}×\mathrm{8}\pi}=\frac{\mathrm{5}}{\mathrm{18}} \\ $$

Commented by TawaTawa last updated on 23/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by TawaTawa last updated on 18/Oct/19

Sir, This first step is not clear to me. How you got it. Help, thanks sir.

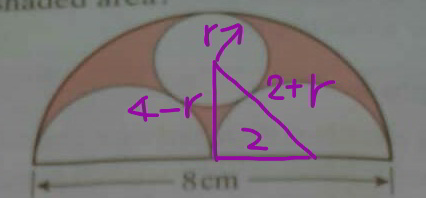
$$\mathrm{Sir},\:\:\mathrm{This}\:\mathrm{first}\:\mathrm{step}\:\mathrm{is}\:\mathrm{not}\:\mathrm{clear}\:\mathrm{to}\:\mathrm{me}.\:\mathrm{How}\:\mathrm{you}\:\mathrm{got}\:\mathrm{it}. \\ $$$$\mathrm{Help},\:\mathrm{thanks}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 18/Oct/19