Question-69494

Question Number 69494 by TawaTawa last updated on 24/Sep/19

Commented by TawaTawa last updated on 24/Sep/19

Please help me find the Area and Perimeter of the shaded part.

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{find}\:\mathrm{the}\:\mathrm{Area}\:\mathrm{and}\:\mathrm{Perimeter}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shaded}\:\mathrm{part}. \\ $$

Commented by mind is power last updated on 24/Sep/19

PB=QD=15−R=15−((15(√3))/2) PQ^⌢ =R.(π/6)=((15π)/6) perimeter=2PB+2BC+PQ^⌢ =2(15−((15(√3))/2))+2.15+((15π)/6)=60−15(√3)+((15π)/6)

$${PB}={QD}=\mathrm{15}−{R}=\mathrm{15}−\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${P}\overset{\frown} {{Q}}={R}.\frac{\pi}{\mathrm{6}}=\frac{\mathrm{15}\pi}{\mathrm{6}} \\ $$$${perimeter}=\mathrm{2}{PB}+\mathrm{2}{BC}+{P}\overset{\frown} {{Q}}=\mathrm{2}\left(\mathrm{15}−\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\mathrm{2}.\mathrm{15}+\frac{\mathrm{15}\pi}{\mathrm{6}}=\mathrm{60}−\mathrm{15}\sqrt{\mathrm{3}}+\frac{\mathrm{15}\pi}{\mathrm{6}} \\ $$

Commented by TawaTawa last updated on 24/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mind is power last updated on 24/Sep/19

BD^2 =AB^2 +AD^2 −2ADABcos(BAD) =15^2 +15^2 −2.15.15.(1/2)=15^2 ⇒BD^2 =15^z ⇒BD=15cm AT=R=ADcos(BAD/2)=((15(√3))/2) let S=area of ABCD S=2.Area ABD=2.(BD.AT)/2=15.((15)/2) (π/6)=(1/(12)).2π S′=Area of Arc of circl =π.r^2 .((π/(6.2π)))=((πr^2 )/(12))=(π/(12)).((15^2 .3)/4)=((225π)/(16)) Area of red=S−S′=((225)/2)−((225π)/(16))=((1800−225π)/(16))

$${BD}^{\mathrm{2}} ={AB}^{\mathrm{2}} +{AD}^{\mathrm{2}} −\mathrm{2}{ADABcos}\left({BAD}\right) \\ $$$$=\mathrm{15}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} −\mathrm{2}.\mathrm{15}.\mathrm{15}.\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{15}^{\mathrm{2}} \Rightarrow{BD}^{\mathrm{2}} =\mathrm{15}^{{z}} \Rightarrow{BD}=\mathrm{15}{cm} \\ $$$${AT}={R}={ADcos}\left({BAD}/\mathrm{2}\right)=\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${let}\:{S}={area}\:{of}\:{ABCD} \\ $$$${S}=\mathrm{2}.{Area}\:{ABD}=\mathrm{2}.\left({BD}.{AT}\right)/\mathrm{2}=\mathrm{15}.\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$\frac{\pi}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{12}}.\mathrm{2}\pi \\ $$$${S}'={Area}\:{of}\:{Arc}\:{of}\:{circl}\:=\pi.{r}^{\mathrm{2}} .\left(\frac{\pi}{\mathrm{6}.\mathrm{2}\pi}\right)=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{12}}=\frac{\pi}{\mathrm{12}}.\frac{\mathrm{15}^{\mathrm{2}} .\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{225}\pi}{\mathrm{16}} \\ $$$${Area}\:{of}\:{red}={S}−{S}'=\frac{\mathrm{225}}{\mathrm{2}}−\frac{\mathrm{225}\pi}{\mathrm{16}}=\frac{\mathrm{1800}−\mathrm{225}\pi}{\mathrm{16}} \\ $$

Commented by TawaTawa last updated on 24/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{what}\:\mathrm{of}\:\mathrm{perimeter}\:? \\ $$

Commented by mind is power last updated on 24/Sep/19

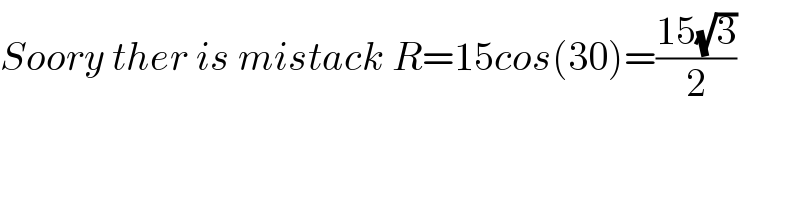
Soory ther is mistack R=15cos(30)=((15(√3))/2)

$${Soory}\:{ther}\:{is}\:{mistack}\:{R}=\mathrm{15}{cos}\left(\mathrm{30}\right)=\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply