Question Number 69594 by ahmadshahhimat775@gmail.com last updated on 25/Sep/19

Answered by MJS last updated on 25/Sep/19
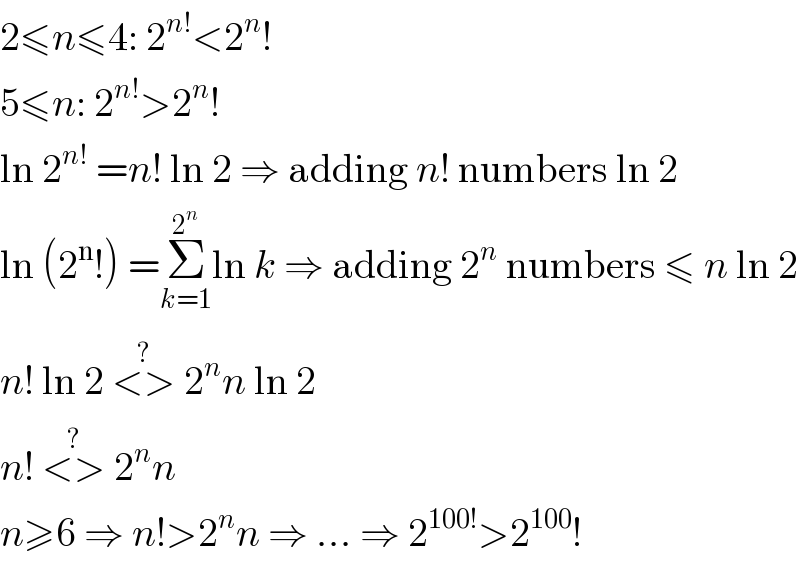
$$\mathrm{2}\leqslant{n}\leqslant\mathrm{4}:\:\mathrm{2}^{{n}!} <\mathrm{2}^{{n}} ! \\ $$$$\mathrm{5}\leqslant{n}:\:\mathrm{2}^{{n}!} >\mathrm{2}^{{n}} ! \\ $$$$\mathrm{ln}\:\mathrm{2}^{{n}!} \:={n}!\:\mathrm{ln}\:\mathrm{2}\:\Rightarrow\:\mathrm{adding}\:{n}!\:\mathrm{numbers}\:\mathrm{ln}\:\mathrm{2} \\ $$$$\mathrm{ln}\:\left(\mathrm{2}^{\mathrm{n}} !\right)\:=\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}^{{n}} } {\sum}}\mathrm{ln}\:{k}\:\Rightarrow\:\mathrm{adding}\:\mathrm{2}^{{n}} \:\mathrm{numbers}\:\leqslant\:{n}\:\mathrm{ln}\:\mathrm{2} \\ $$$${n}!\:\mathrm{ln}\:\mathrm{2}\:\overset{?} {<>}\:\mathrm{2}^{{n}} {n}\:\mathrm{ln}\:\mathrm{2} \\ $$$${n}!\:\overset{?} {<>}\:\mathrm{2}^{{n}} {n} \\ $$$${n}\geqslant\mathrm{6}\:\Rightarrow\:{n}!>\mathrm{2}^{{n}} {n}\:\Rightarrow\:…\:\Rightarrow\:\mathrm{2}^{\mathrm{100}!} >\mathrm{2}^{\mathrm{100}} ! \\ $$
