Question-69710

Question Number 69710 by ahmadshahhimat775@gmail.com last updated on 26/Sep/19

Commented by mathmax by abdo last updated on 27/Sep/19

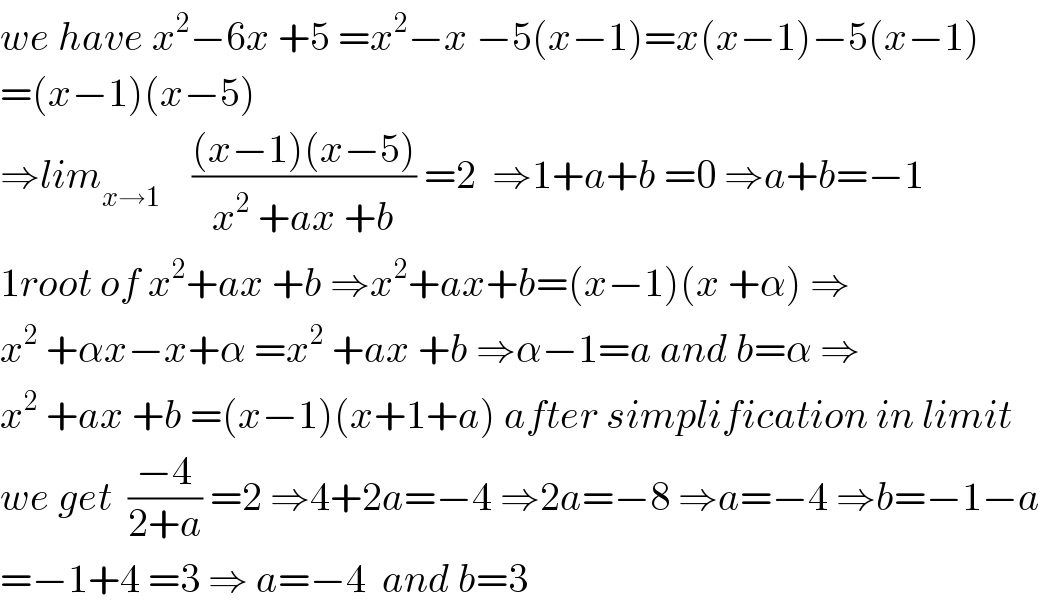
we have x^2 −6x +5 =x^2 −x −5(x−1)=x(x−1)−5(x−1) =(x−1)(x−5) ⇒lim_(x→1) (((x−1)(x−5))/(x^2 +ax +b)) =2 ⇒1+a+b =0 ⇒a+b=−1 1root of x^2 +ax +b ⇒x^2 +ax+b=(x−1)(x +α) ⇒ x^2 +αx−x+α =x^2 +ax +b ⇒α−1=a and b=α ⇒ x^2 +ax +b =(x−1)(x+1+a) after simplification in limit we get ((−4)/(2+a)) =2 ⇒4+2a=−4 ⇒2a=−8 ⇒a=−4 ⇒b=−1−a =−1+4 =3 ⇒ a=−4 and b=3

$${we}\:{have}\:{x}^{\mathrm{2}} −\mathrm{6}{x}\:+\mathrm{5}\:={x}^{\mathrm{2}} −{x}\:−\mathrm{5}\left({x}−\mathrm{1}\right)={x}\left({x}−\mathrm{1}\right)−\mathrm{5}\left({x}−\mathrm{1}\right) \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{5}\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} \:\:\:\:\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{5}\right)}{{x}^{\mathrm{2}} \:+{ax}\:+{b}}\:=\mathrm{2}\:\:\Rightarrow\mathrm{1}+{a}+{b}\:=\mathrm{0}\:\Rightarrow{a}+{b}=−\mathrm{1} \\ $$$$\mathrm{1}{root}\:{of}\:{x}^{\mathrm{2}} +{ax}\:+{b}\:\Rightarrow{x}^{\mathrm{2}} +{ax}+{b}=\left({x}−\mathrm{1}\right)\left({x}\:+\alpha\right)\:\Rightarrow \\ $$$${x}^{\mathrm{2}} \:+\alpha{x}−{x}+\alpha\:={x}^{\mathrm{2}} \:+{ax}\:+{b}\:\Rightarrow\alpha−\mathrm{1}={a}\:{and}\:{b}=\alpha\:\Rightarrow \\ $$$${x}^{\mathrm{2}} \:+{ax}\:+{b}\:=\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}+{a}\right)\:{after}\:{simplification}\:{in}\:{limit} \\ $$$${we}\:{get}\:\:\frac{−\mathrm{4}}{\mathrm{2}+{a}}\:=\mathrm{2}\:\Rightarrow\mathrm{4}+\mathrm{2}{a}=−\mathrm{4}\:\Rightarrow\mathrm{2}{a}=−\mathrm{8}\:\Rightarrow{a}=−\mathrm{4}\:\Rightarrow{b}=−\mathrm{1}−{a} \\ $$$$=−\mathrm{1}+\mathrm{4}\:=\mathrm{3}\:\Rightarrow\:{a}=−\mathrm{4}\:\:{and}\:{b}=\mathrm{3} \\ $$

Answered by $@ty@m123 last updated on 26/Sep/19

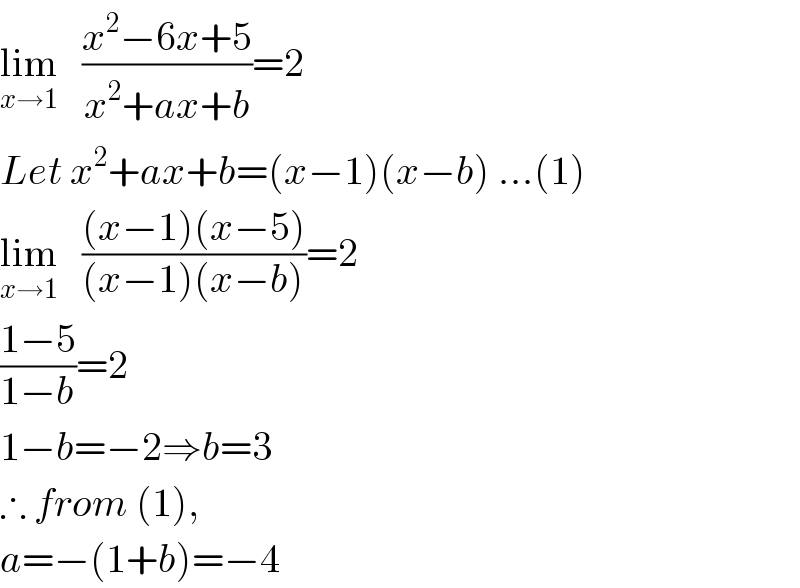
lim_(x→1) ((x^2 −6x+5)/(x^2 +ax+b))=2 Let x^2 +ax+b=(x−1)(x−b) ...(1) lim_(x→1) (((x−1)(x−5))/((x−1)(x−b)))=2 ((1−5)/(1−b))=2 1−b=−2⇒b=3 ∴ from (1), a=−(1+b)=−4

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:\:\frac{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}}{{x}^{\mathrm{2}} +{ax}+{b}}=\mathrm{2} \\ $$$${Let}\:{x}^{\mathrm{2}} +{ax}+{b}=\left({x}−\mathrm{1}\right)\left({x}−{b}\right)\:…\left(\mathrm{1}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:\:\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{5}\right)}{\left({x}−\mathrm{1}\right)\left({x}−{b}\right)}=\mathrm{2} \\ $$$$\frac{\mathrm{1}−\mathrm{5}}{\mathrm{1}−{b}}=\mathrm{2} \\ $$$$\mathrm{1}−{b}=−\mathrm{2}\Rightarrow{b}=\mathrm{3} \\ $$$$\therefore\:{from}\:\left(\mathrm{1}\right), \\ $$$${a}=−\left(\mathrm{1}+{b}\right)=−\mathrm{4} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply