Menu Close

Question-69741

Tinku Tara 0 Comments
Pin




Question Number 69741 by ajfour last updated on 27/Sep/19
Commented by mr W last updated on 27/Sep/19
Commented by mr W last updated on 27/Sep/19
Commented by mr W last updated on 27/Sep/19
Commented by ajfour last updated on 27/Sep/19
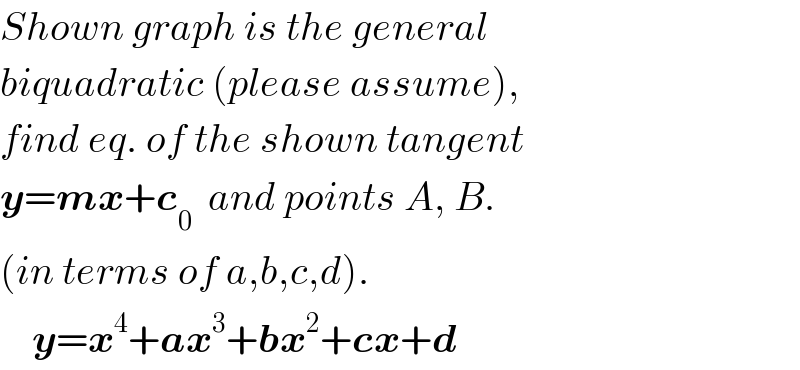
Shown graph is the general biquadratic (please assume), find eq. of the shown tangent y=mx+c_0 and points A, B. (in terms of a,b,c,d). y=x^4 +ax^3 +bx^2 +cx+d
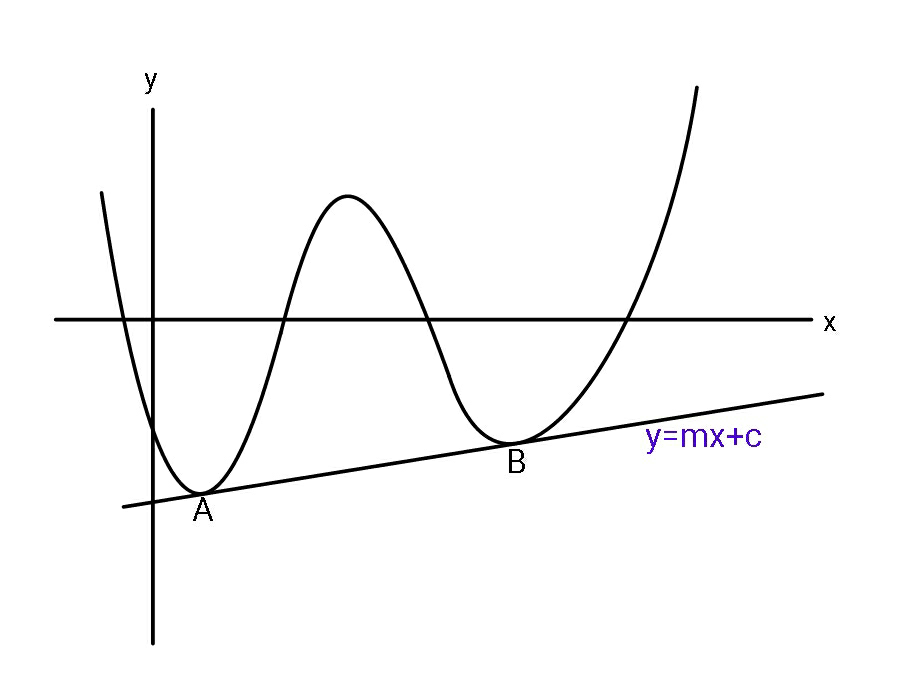
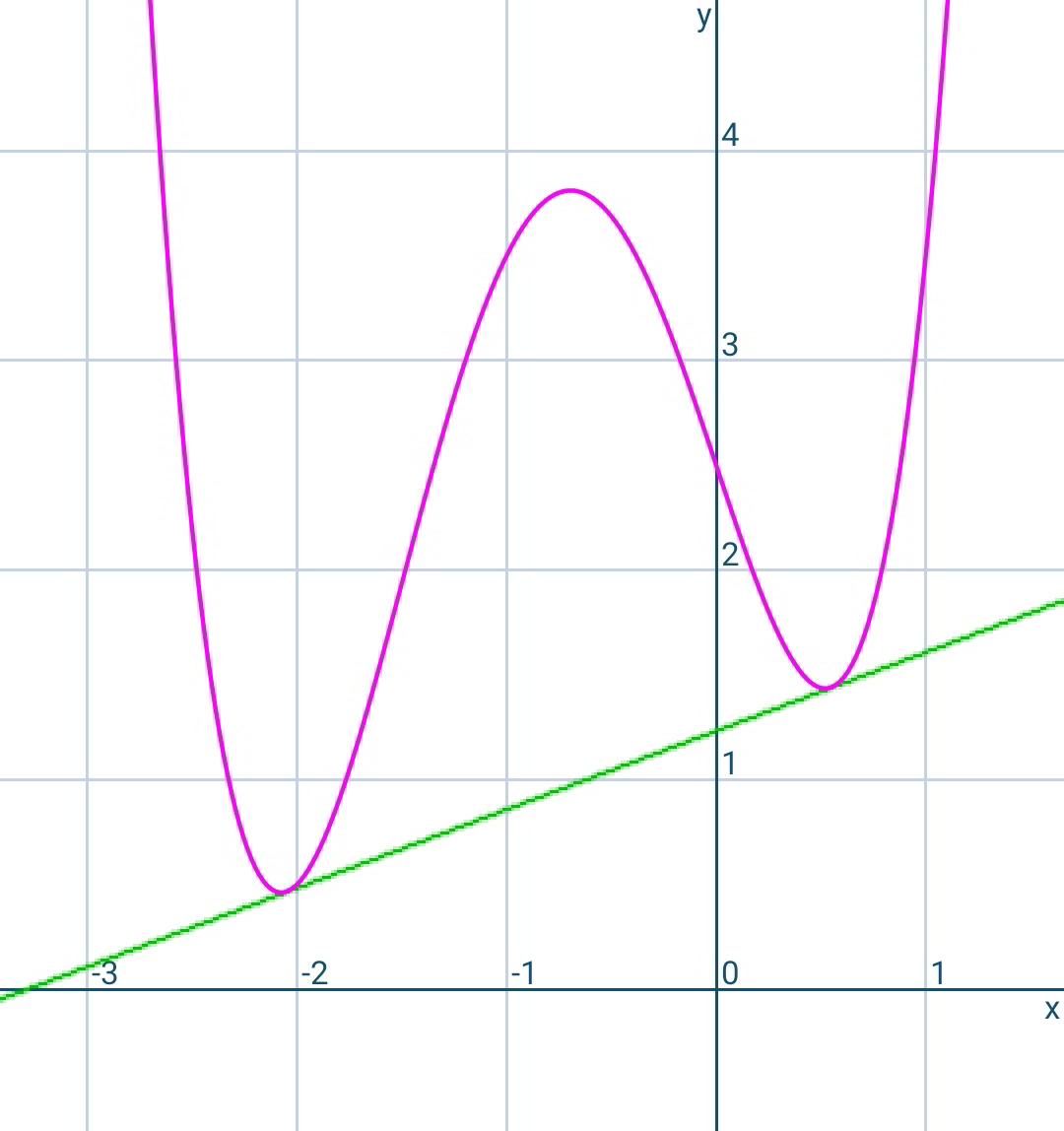
$${Shown}\:{graph}\:{is}\:{the}\:{general} \\ $$$${biquadratic}\:\left({please}\:{assume}\right), \\ $$$${find}\:{eq}.\:{of}\:{the}\:{shown}\:{tangent} \\ $$$$\boldsymbol{{y}}=\boldsymbol{{mx}}+\boldsymbol{{c}}_{\mathrm{0}} \:\:{and}\:{points}\:{A},\:{B}. \\ $$$$\left({in}\:{terms}\:{of}\:{a},{b},{c},{d}\right). \\ $$$$\:\:\:\:\boldsymbol{{y}}=\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{ax}}^{\mathrm{3}} +\boldsymbol{{bx}}^{\mathrm{2}} +\boldsymbol{{cx}}+\boldsymbol{{d}} \\ $$
Answered by mr W last updated on 28/Sep/19
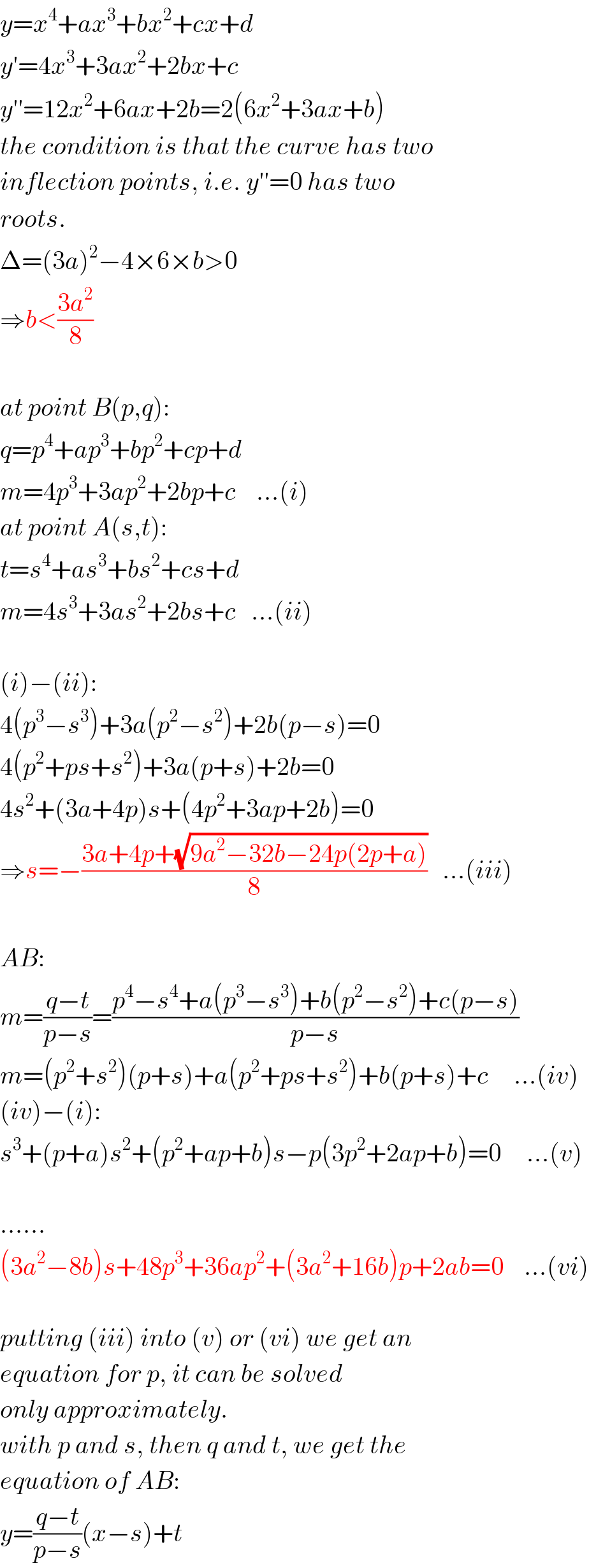
y=x^4 +ax^3 +bx^2 +cx+d y′=4x^3 +3ax^2 +2bx+c y′′=12x^2 +6ax+2b=2(6x^2 +3ax+b) the condition is that the curve has two inflection points, i.e. y′′=0 has two roots. Δ=(3a)^2 −4×6×b>0 ⇒b<((3a^2 )/8) at point B(p,q): q=p^4 +ap^3 +bp^2 +cp+d m=4p^3 +3ap^2 +2bp+c ...(i) at point A(s,t): t=s^4 +as^3 +bs^2 +cs+d m=4s^3 +3as^2 +2bs+c ...(ii) (i)−(ii): 4(p^3 −s^3 )+3a(p^2 −s^2 )+2b(p−s)=0 4(p^2 +ps+s^2 )+3a(p+s)+2b=0 4s^2 +(3a+4p)s+(4p^2 +3ap+2b)=0 ⇒s=−((3a+4p+(√(9a^2 −32b−24p(2p+a))))/8) ...(iii) AB: m=((q−t)/(p−s))=((p^4 −s^4 +a(p^3 −s^3 )+b(p^2 −s^2 )+c(p−s))/(p−s)) m=(p^2 +s^2 )(p+s)+a(p^2 +ps+s^2 )+b(p+s)+c ...(iv) (iv)−(i): s^3 +(p+a)s^2 +(p^2 +ap+b)s−p(3p^2 +2ap+b)=0 ...(v) ...... (3a^2 −8b)s+48p^3 +36ap^2 +(3a^2 +16b)p+2ab=0 ...(vi) putting (iii) into (v) or (vi) we get an equation for p, it can be solved only approximately. with p and s, then q and t, we get the equation of AB: y=((q−t)/(p−s))(x−s)+t
$${y}={x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${y}'=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c} \\ $$$${y}''=\mathrm{12}{x}^{\mathrm{2}} +\mathrm{6}{ax}+\mathrm{2}{b}=\mathrm{2}\left(\mathrm{6}{x}^{\mathrm{2}} +\mathrm{3}{ax}+{b}\right) \\ $$$${the}\:{condition}\:{is}\:{that}\:{the}\:{curve}\:{has}\:{two} \\ $$$${inflection}\:{points},\:{i}.{e}.\:{y}''=\mathrm{0}\:{has}\:{two} \\ $$$${roots}. \\ $$$$\Delta=\left(\mathrm{3}{a}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{6}×{b}>\mathrm{0} \\ $$$$\Rightarrow{b}<\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$ \\ $$$${at}\:{point}\:{B}\left({p},{q}\right): \\ $$$${q}={p}^{\mathrm{4}} +{ap}^{\mathrm{3}} +{bp}^{\mathrm{2}} +{cp}+{d} \\ $$$${m}=\mathrm{4}{p}^{\mathrm{3}} +\mathrm{3}{ap}^{\mathrm{2}} +\mathrm{2}{bp}+{c}\:\:\:\:…\left({i}\right) \\ $$$${at}\:{point}\:{A}\left({s},{t}\right): \\ $$$${t}={s}^{\mathrm{4}} +{as}^{\mathrm{3}} +{bs}^{\mathrm{2}} +{cs}+{d} \\ $$$${m}=\mathrm{4}{s}^{\mathrm{3}} +\mathrm{3}{as}^{\mathrm{2}} +\mathrm{2}{bs}+{c}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{4}\left({p}^{\mathrm{3}} −{s}^{\mathrm{3}} \right)+\mathrm{3}{a}\left({p}^{\mathrm{2}} −{s}^{\mathrm{2}} \right)+\mathrm{2}{b}\left({p}−{s}\right)=\mathrm{0} \\ $$$$\mathrm{4}\left({p}^{\mathrm{2}} +{ps}+{s}^{\mathrm{2}} \right)+\mathrm{3}{a}\left({p}+{s}\right)+\mathrm{2}{b}=\mathrm{0} \\ $$$$\mathrm{4}{s}^{\mathrm{2}} +\left(\mathrm{3}{a}+\mathrm{4}{p}\right){s}+\left(\mathrm{4}{p}^{\mathrm{2}} +\mathrm{3}{ap}+\mathrm{2}{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{s}=−\frac{\mathrm{3}{a}+\mathrm{4}{p}+\sqrt{\mathrm{9}{a}^{\mathrm{2}} −\mathrm{32}{b}−\mathrm{24}{p}\left(\mathrm{2}{p}+{a}\right)}}{\mathrm{8}}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$${AB}: \\ $$$${m}=\frac{{q}−{t}}{{p}−{s}}=\frac{{p}^{\mathrm{4}} −{s}^{\mathrm{4}} +{a}\left({p}^{\mathrm{3}} −{s}^{\mathrm{3}} \right)+{b}\left({p}^{\mathrm{2}} −{s}^{\mathrm{2}} \right)+{c}\left({p}−{s}\right)}{{p}−{s}} \\ $$$${m}=\left({p}^{\mathrm{2}} +{s}^{\mathrm{2}} \right)\left({p}+{s}\right)+{a}\left({p}^{\mathrm{2}} +{ps}+{s}^{\mathrm{2}} \right)+{b}\left({p}+{s}\right)+{c}\:\:\:\:\:…\left({iv}\right) \\ $$$$\left({iv}\right)−\left({i}\right): \\ $$$${s}^{\mathrm{3}} +\left({p}+{a}\right){s}^{\mathrm{2}} +\left({p}^{\mathrm{2}} +{ap}+{b}\right){s}−{p}\left(\mathrm{3}{p}^{\mathrm{2}} +\mathrm{2}{ap}+{b}\right)=\mathrm{0}\:\:\:\:\:…\left({v}\right) \\ $$$$ \\ $$$$…… \\ $$$$\left(\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}\right){s}+\mathrm{48}{p}^{\mathrm{3}} +\mathrm{36}{ap}^{\mathrm{2}} +\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{16}{b}\right){p}+\mathrm{2}{ab}=\mathrm{0}\:\:\:\:…\left({vi}\right) \\ $$$$ \\ $$$${putting}\:\left({iii}\right)\:{into}\:\left({v}\right)\:{or}\:\left({vi}\right)\:{we}\:{get}\:{an} \\ $$$${equation}\:{for}\:{p},\:{it}\:{can}\:{be}\:{solved} \\ $$$${only}\:{approximately}. \\ $$$${with}\:{p}\:{and}\:{s},\:{then}\:{q}\:{and}\:{t},\:{we}\:{get}\:{the} \\ $$$${equation}\:{of}\:{AB}: \\ $$$${y}=\frac{{q}−{t}}{{p}−{s}}\left({x}−{s}\right)+{t} \\ $$
Commented by mr W last updated on 28/Sep/19
Commented by ajfour last updated on 28/Sep/19
Thanks Sir, please view my attempt..
$${Thanks}\:{Sir},\:{please}\:{view}\:{my}\: \\ $$$${attempt}.. \\ $$
Answered by ajfour last updated on 28/Sep/19
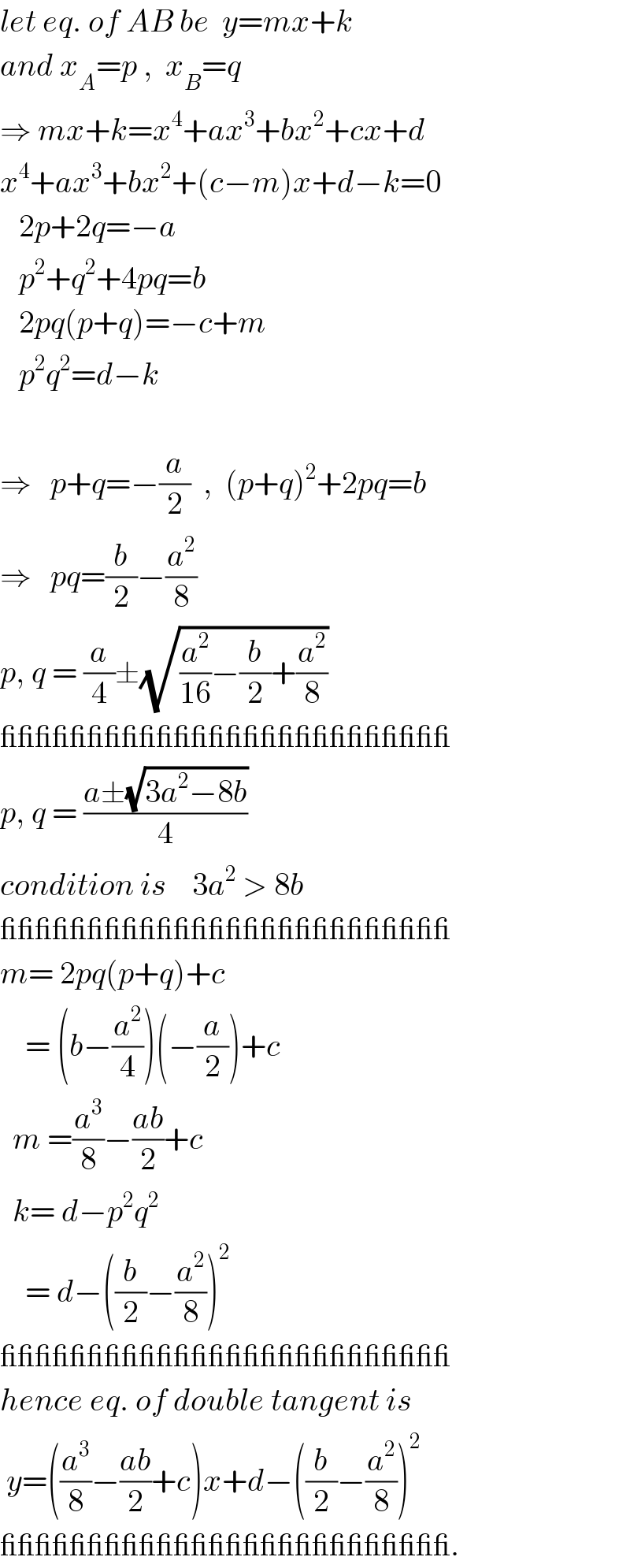
let eq. of AB be y=mx+k and x_A =p , x_B =q ⇒ mx+k=x^4 +ax^3 +bx^2 +cx+d x^4 +ax^3 +bx^2 +(c−m)x+d−k=0 2p+2q=−a p^2 +q^2 +4pq=b 2pq(p+q)=−c+m p^2 q^2 =d−k ⇒ p+q=−(a/2) , (p+q)^2 +2pq=b ⇒ pq=(b/2)−(a^2 /8) p, q = (a/4)±(√((a^2 /(16))−(b/2)+(a^2 /8))) __________________________ p, q = ((a±(√(3a^2 −8b)))/4) condition is 3a^2 > 8b __________________________ m= 2pq(p+q)+c = (b−(a^2 /4))(−(a/2))+c m =(a^3 /8)−((ab)/2)+c k= d−p^2 q^2 = d−((b/2)−(a^2 /8))^2 __________________________ hence eq. of double tangent is y=((a^3 /8)−((ab)/2)+c)x+d−((b/2)−(a^2 /8))^2 __________________________.
$${let}\:{eq}.\:{of}\:{AB}\:{be}\:\:{y}={mx}+{k} \\ $$$${and}\:{x}_{{A}} ={p}\:,\:\:{x}_{{B}} ={q} \\ $$$$\Rightarrow\:{mx}+{k}={x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +\left({c}−{m}\right){x}+{d}−{k}=\mathrm{0} \\ $$$$\:\:\:\mathrm{2}{p}+\mathrm{2}{q}=−{a} \\ $$$$\:\:\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\mathrm{4}{pq}={b} \\ $$$$\:\:\:\mathrm{2}{pq}\left({p}+{q}\right)=−{c}+{m} \\ $$$$\:\:\:{p}^{\mathrm{2}} {q}^{\mathrm{2}} ={d}−{k} \\ $$$$ \\ $$$$\Rightarrow\:\:\:{p}+{q}=−\frac{{a}}{\mathrm{2}}\:\:,\:\:\left({p}+{q}\right)^{\mathrm{2}} +\mathrm{2}{pq}={b} \\ $$$$\Rightarrow\:\:\:{pq}=\frac{{b}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{8}} \\ $$$${p},\:{q}\:=\:\frac{{a}}{\mathrm{4}}\pm\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{16}}−\frac{{b}}{\mathrm{2}}+\frac{{a}^{\mathrm{2}} }{\mathrm{8}}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${p},\:{q}\:=\:\frac{{a}\pm\sqrt{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}}{\mathrm{4}} \\ $$$${condition}\:{is}\:\:\:\:\mathrm{3}{a}^{\mathrm{2}} \:>\:\mathrm{8}{b} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${m}=\:\mathrm{2}{pq}\left({p}+{q}\right)+{c} \\ $$$$\:\:\:\:=\:\left({b}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right)\left(−\frac{{a}}{\mathrm{2}}\right)+{c} \\ $$$$\:\:{m}\:=\frac{{a}^{\mathrm{3}} }{\mathrm{8}}−\frac{{ab}}{\mathrm{2}}+{c} \\ $$$$\:\:{k}=\:{d}−{p}^{\mathrm{2}} {q}^{\mathrm{2}} \\ $$$$\:\:\:\:=\:{d}−\left(\frac{{b}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\right)^{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${hence}\:{eq}.\:{of}\:{double}\:{tangent}\:{is} \\ $$$$\:{y}=\left(\frac{{a}^{\mathrm{3}} }{\mathrm{8}}−\frac{{ab}}{\mathrm{2}}+{c}\right){x}+{d}−\left(\frac{{b}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\right)^{\mathrm{2}} \: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$
Commented by mr W last updated on 28/Sep/19
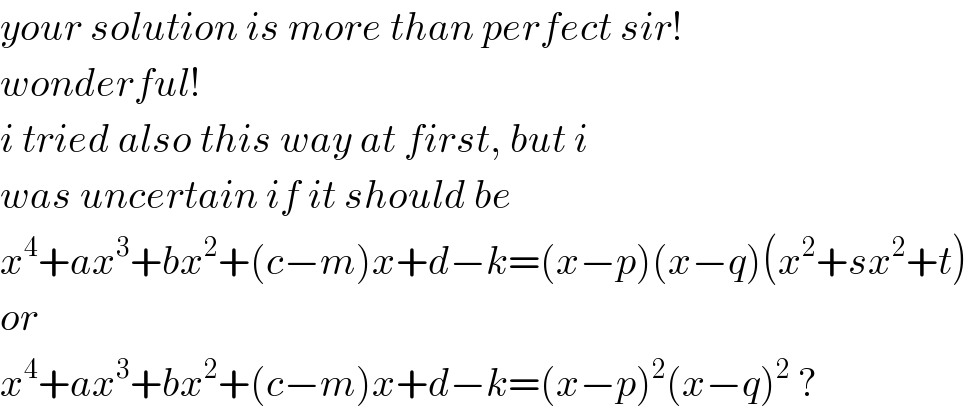
your solution is more than perfect sir! wonderful! i tried also this way at first, but i was uncertain if it should be x^4 +ax^3 +bx^2 +(c−m)x+d−k=(x−p)(x−q)(x^2 +sx^2 +t) or x^4 +ax^3 +bx^2 +(c−m)x+d−k=(x−p)^2 (x−q)^2 ?
$${your}\:{solution}\:{is}\:{more}\:{than}\:{perfect}\:{sir}! \\ $$$${wonderful}! \\ $$$${i}\:{tried}\:{also}\:{this}\:{way}\:{at}\:{first},\:{but}\:{i} \\ $$$${was}\:{uncertain}\:{if}\:{it}\:{should}\:{be} \\ $$$${x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +\left({c}−{m}\right){x}+{d}−{k}=\left({x}−{p}\right)\left({x}−{q}\right)\left({x}^{\mathrm{2}} +{sx}^{\mathrm{2}} +{t}\right) \\ $$$${or} \\ $$$${x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +\left({c}−{m}\right){x}+{d}−{k}=\left({x}−{p}\right)^{\mathrm{2}} \left({x}−{q}\right)^{\mathrm{2}} \:? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *